[LeetCode] 1560. Most Visited Sector in a Circular Track

Given an integer n and an integer array rounds. We have a circular track which consists of n sectors labeled from 1 to n. A marathon will be held on this track, the marathon consists of m rounds. The ith round starts at sector rounds[i - 1] and ends at sector rounds[i]. For example, round 1 starts at sector rounds[0] and ends at sector rounds[1]

Return an array of the most visited sectors sorted in ascending order.

Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).

Example 1:

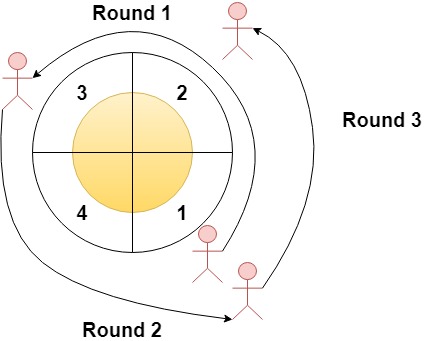
Input: n = 4, rounds = [1,3,1,2]
Output: [1,2]
Explanation: The marathon starts at sector 1. The order of the visited sectors is as follows:
1 --> 2 --> 3 (end of round 1) --> 4 --> 1 (end of round 2) --> 2 (end of round 3 and the marathon)
We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.

Example 2:

Input: n = 2, rounds = [2,1,2,1,2,1,2,1,2]
Output: [2]

Example 3:

Input: n = 7, rounds = [1,3,5,7]
Output: [1,2,3,4,5,6,7]

Constraints:

• 2 <= n <= 100
• 1 <= m <= 100
• rounds.length == m + 1
• 1 <= rounds[i] <= n
• rounds[i] != rounds[i + 1] for 0 <= i < m

圆形赛道上经过次数最多的扇区。

给你一个整数 n 和一个整数数组 rounds 。有一条圆形赛道由 n 个扇区组成，扇区编号从 1 到 n 。现将在这条赛道上举办一场马拉松比赛，该马拉松全程由 m 个阶段组成。其中，第 i 个阶段将会从扇区 rounds[i - 1] 开始，到扇区 rounds[i] 结束。举例来说，第 1 阶段从 rounds[0] 开始，到 rounds[1] 结束。

请你以数组形式返回经过次数最多的那几个扇区，按扇区编号 升序 排列。

注意，赛道按扇区编号升序逆时针形成一个圆（请参见第一个示例）。

这是一道模拟题，但是我们可以不需要按照题意一步步地模拟整个流程。注意这道题的👎比👍要多，估计是因为题意说的不是非常清楚的关系吧，我也是看了好几遍才明白题目的例子。注意整个比赛的起点并不一定是从 index = 1 的那个扇形开始的。我们无需关注他是从哪个扇形开始的，只需要关注每个阶段的比赛到底是涉及哪些扇形即可。

这里我把题意再解释一下，比如例子一，n = 4, rounds = [1,3,1,2]，n 就是扇形的个数；rounds 数组里，我们需要把每两个数字理解为起点 -> 终点，即 1 - 3 - 1 - 2。比如

• 1 - 3 意思是起点是在扇形 1，终点是扇形 3
• 3 - 1 意思是起点是在扇形 3，终点是扇形 1
• 1 - 2 意思是起点是在扇形 1，终点是扇形 2

经过若干次的比赛之后，我们只需要看起点 start 和终点 end 分别在扇形的什么位置，然后从 start 逆时针走到 end，中间经过的所有扇形，就是经过次数最多的扇形了。因为从第二场比赛开始，每场比赛的起点都是上一场比赛的终点，中间不存在跳过某个扇形的情况。所以我们直接看数组的第一个元素 start 和最后一个元素 end 即可。如果 start < end，很好理解，那么就是遍历 [start, end] 这部分；但是如果 start > end，我们就需要分两段计算，因为跨过了 index = 1 的那个扇形。具体参见代码。

时间O(n)

空间O(1)

Java实现

class Solution {
    public List<Integer> mostVisited(int n, int[] rounds) {
        List<Integer> res = new ArrayList<>();
        int len = rounds.length;
        int start = rounds[0];
        int end = rounds[len - 1];
        if (start <= end) {
            for (int i = start; i <= end; i++) {
                res.add(i);
            }
        } else {
            for (int i = 1; i <= end; i++) {
                res.add(i);
            }
            for (int i = start; i <= n; i++) {
                res.add(i);
            }
        }
        return res;
    }
}

 

LeetCode 题目总结