[LeetCode] 2013. Detect Squares

You are given a stream of points on the X-Y plane. Design an algorithm that:

• Adds new points from the stream into a data structure. Duplicate points are allowed and should be treated as different points.
• Given a query point, counts the number of ways to choose three points from the data structure such that the three points and the query point form an axis-aligned square with positive area.

An axis-aligned square is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.

Implement the DetectSquares class:

• DetectSquares() Initializes the object with an empty data structure.
• void add(int[] point) Adds a new point point = [x, y] to the data structure.
• int count(int[] point) Counts the number of ways to form axis-aligned squares with point point = [x, y] as described above.

Example 1:

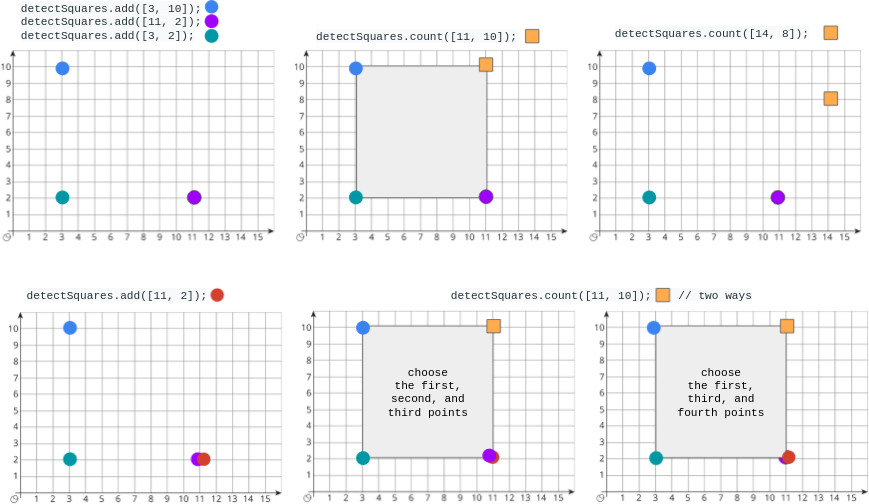
Input
["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
Output
[null, null, null, null, 1, 0, null, 2]

Explanation
DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // return 1. You can choose:
                               //   - The first, second, and third points
detectSquares.count([14, 8]);  // return 0. The query point cannot form a square with any points in the data structure.
detectSquares.add([11, 2]);    // Adding duplicate points is allowed.
detectSquares.count([11, 10]); // return 2. You can choose:
                               //   - The first, second, and third points
                               //   - The first, third, and fourth points

Constraints:

• point.length == 2
• 0 <= x, y <= 1000
• At most 3000 calls in total will be made to add and count.

检测正方形。

给你一个在 X-Y 平面上的点构成的数据流。设计一个满足下述要求的算法：

添加 一个在数据流中的新点到某个数据结构中。可以添加 重复 的点，并会视作不同的点进行处理。
给你一个查询点，请你从数据结构中选出三个点，使这三个点和查询点一同构成一个 面积为正 的 轴对齐正方形 ，统计 满足该要求的方案数目。
轴对齐正方形 是一个正方形，除四条边长度相同外，还满足每条边都与 x-轴 或 y-轴 平行或垂直。

实现 DetectSquares 类：

DetectSquares() 使用空数据结构初始化对象
void add(int[] point) 向数据结构添加一个新的点 point = [x, y]
int count(int[] point) 统计按上述方式与点 point = [x, y] 共同构造 轴对齐正方形 的方案数。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/detect-squares
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这是一道设计题。这里我提供一个 hashmap + arraylist 的做法。因为点是通过数据流给出的，对于一开始给出的点，我们需要用一个数据结构把他存起来，这里不难想到是用 hashmap 存，这里我将给出的点同时存在一个 arraylist 里，之后我会说为什么。

我们在处理 count 函数的时候，对于 count 函数给出的点，我们要找到底这个点能形成多少个正方形。这里我将给出的点假设为正方形对角线上的一个点 A（x, y），然后我去 hashmap 里遍历其他所有的点 B（px, py），假设 A - B 是最后能形成的正方形的其中一条对角线。所以如果点 B 的横坐标 = A 的横坐标（px == x），或者 B 的纵坐标 = A 的纵坐标（py == y），则说明两者无法构成对角线；如果两者横坐标的差 != 纵坐标的差，说明两者也无法构成一个正方形。排除这些条件后，说明 A - B 可以成为某个正方形的对角线。假设 A 是左上角的点，B 是右下角的点，那么另外两个点的坐标应该是（x, py）和（px, y）。那么最后这四个点能形成的正方形的个数 = （x, py）的个数 * （px, y）的个数。

这里我解释一下为什么正方形的个数 = （x, py）的个数 * （px, y）的个数。因为 count 函数的 input 是其中一个点的坐标，我们遍历 arraylist 的时候，也只能锁定第二个点，所以正方形个数 = 另外两个点各自的出现次数的乘积。因为 arraylist 存在重复元素，所以在遍历 arraylist 的时候，很有可能发现第二个点的坐标出现了多次，所以不会漏掉计算。

时间

add() - O(1)

count() - O(n) - 取决于 arraylist 里已经存入了多少元素

空间O(n)

Java实现

class DetectSquares {
    List<int[]> coordinates;
    Map<String, Integer> map;

    public DetectSquares() {
        coordinates = new ArrayList<>();
        map = new HashMap<>();
    }
    
    public void add(int[] point) {
        coordinates.add(point);
        String key = point[0] + "," + point[1];
        map.put(key, map.getOrDefault(key, 0) + 1);
    }
    
    public int count(int[] point) {
        int res = 0;
        int px = point[0], py = point[1];
        for (int[] c : coordinates) {
            int x = c[0], y = c[1];
            if (px == x || py == y || (Math.abs(px - x) != Math.abs(py - y))) {
                continue;
            }
            res += map.getOrDefault(x + "," + py, 0) * map.getOrDefault(px + "," + y, 0);
        }
        return res;
    }
}

/**
 * Your DetectSquares object will be instantiated and called as such:
 * DetectSquares obj = new DetectSquares();
 * obj.add(point);
 * int param_2 = obj.count(point);
 */

 

LeetCode 题目总结