[LeetCode] 894. All Possible Full Binary Trees

Given an integer n, return a list of all possible full binary trees with n nodes. Each node of each tree in the answer must have Node.val == 0.

Each element of the answer is the root node of one possible tree. You may return the final list of trees in any order.

A full binary tree is a binary tree where each node has exactly 0 or 2 children.

Example 1:

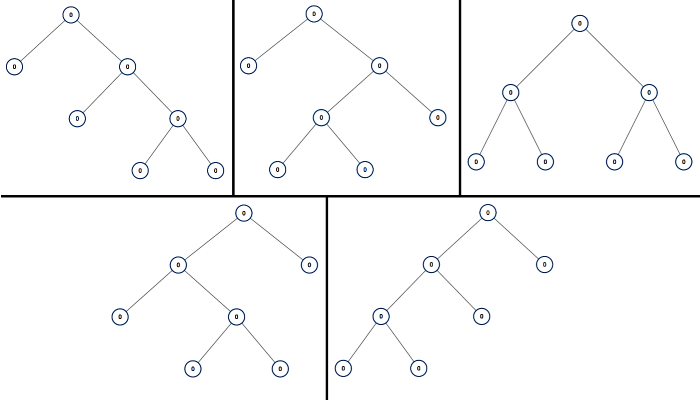
Input: n = 7
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]

Example 2:

Input: n = 3
Output: [[0,0,0]]

Constraints:

• 1 <= n <= 20

所有可能的真二叉树。

给你一个整数 n ，请你找出所有可能含 n 个节点的 真二叉树 ，并以列表形式返回。答案中每棵树的每个节点都必须符合 Node.val == 0 。

答案的每个元素都是一棵真二叉树的根节点。你可以按 任意顺序 返回最终的真二叉树列表。

真二叉树 是一类二叉树，树中每个节点恰好有 0 或 2 个子节点。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/all-possible-full-binary-trees
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路是 dfs + memo，记忆化递归。

注意真二叉树的定义，每个 node 只有 0 个或 2 个子节点，那么对于任意一棵真二叉树而言，他的 node 总个数应该只能为奇数。不过这里我们需要处理一个 corner case，就是当 n == 1 的时候，我们可以得到一棵树，只有一个根节点。对于其他 n > 1 的情况，我们思考一下，此时左子树应该有 i 个节点，i 为奇数；那么右子树应该有 n - 1 - i 个节点。我们需要遍历所有情况，把 i 和 n - 1 - i 的不同组合都找到，并用一个 hashmap 存下来，这样 n 足够大的时候，我们就省去重复计算。

时间O(2^n) - 卡特兰数

空间O(2^n) - 也应该有这么多种结果

Java实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    Map<Integer, List<TreeNode>> memo = new HashMap();

    public List<TreeNode> allPossibleFBT(int n) {
        if (!memo.containsKey(n)) {
            List<TreeNode> res = new ArrayList<>();
            // corner case
            if (n == 1) {
                res.add(new TreeNode(0));
            } else if (n % 2 == 1) {
                for (int i = 1; i < n - 1; i += 2) {
                    int j = n - 1 - i;
                    for (TreeNode left : allPossibleFBT(i)) {
                        for (TreeNode right : allPossibleFBT(j)) {
                            TreeNode root = new TreeNode(0);
                            root.left = left;
                            root.right = right;
                            res.add(root);
                        }
                    }
                }
            }
            memo.put(n, res);
        }
        return memo.get(n);
    }
}

 

LeetCode 题目总结