[LeetCode] 1557. Minimum Number of Vertices to Reach All Nodes

Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.

Find the smallest set of vertices from which all nodes in the graph are reachable. It's guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

Example 1:

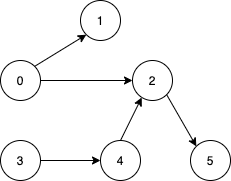
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

Example 2:

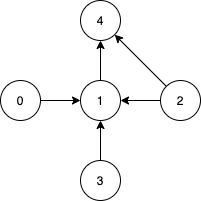
Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.

Constraints:

• 2 <= n <= 10^5
• 1 <= edges.length <= min(10^5, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi < n
• All pairs (fromi, toi) are distinct.

可以到达所有点的最少点数目。

给你一个 有向无环图 ， n 个节点编号为 0 到 n-1 ，以及一个边数组 edges ，其中 edges[i] = [fromi, toi] 表示一条从点  fromi 到点 toi 的有向边。

找到最小的点集使得从这些点出发能到达图中所有点。题目保证解存在且唯一。

你可以以任意顺序返回这些节点编号。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-number-of-vertices-to-reach-all-nodes
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这是一道图论的题。题目要求输出一个尽可能小的列表，但是要包含所有的起点，通过这些起点可以最终到达有向图中所有的点。思路是统计图中所有入度为 0 的点，因为入度为 0 的点，是无法通过其他点走到的，所以必须要加入结果集；入度不为 0 的点，说明总有办法从其他某个点最终遍历到他，这些点就无须加入结果集。

时间O(n)

空间O(n) - output

Java实现

class Solution {
    public List<Integer> findSmallestSetOfVertices(int n, List<List<Integer>> edges) {
        int[] indegree = new int[n];
        for (List<Integer> edge : edges) {
            int to = edge.get(1);
            indegree[to]++;
        }
        
        List<Integer> res = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (indegree[i] == 0) {
                res.add(i);
            }
        }
        return res;
    }
}

 

LeetCode 题目总结