[LeetCode] 1031. Maximum Sum of Two Non-Overlapping Subarrays

Given an integer array nums and two integers firstLen and secondLen, return the maximum sum of elements in two non-overlapping subarrays with lengths firstLen and secondLen.

The array with length firstLen could occur before or after the array with length secondLen, but they have to be non-overlapping.

A subarray is a contiguous part of an array.

Example 1:
Input: nums = [0,6,5,2,2,5,1,9,4], firstLen = 1, secondLen = 2
Output: 20
Explanation: One choice of subarrays is [9] with length 1, and [6,5] with length 2.

Example 2:
Input: nums = [3,8,1,3,2,1,8,9,0], firstLen = 3, secondLen = 2
Output: 29
Explanation: One choice of subarrays is [3,8,1] with length 3, and [8,9] with length 2.

Example 3:
Input: nums = [2,1,5,6,0,9,5,0,3,8], firstLen = 4, secondLen = 3
Output: 31
Explanation: One choice of subarrays is [5,6,0,9] with length 4, and [0,3,8] with length 3.

Constraints:
1 <= firstLen, secondLen <= 1000
2 <= firstLen + secondLen <= 1000
firstLen + secondLen <= nums.length <= 1000
0 <= nums[i] <= 1000

两个非重叠子数组的最大和。

给你一个整数数组 nums 和两个整数 firstLen 和 secondLen，请你找出并返回两个非重叠 子数组 中元素的最大和，长度分别为 firstLen 和 secondLen 。

长度为 firstLen 的子数组可以出现在长为 secondLen 的子数组之前或之后，但二者必须是不重叠的。

子数组是数组的一个 连续 部分。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/maximum-sum-of-two-non-overlapping-subarrays
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

思路是前缀和。我参考了这个帖子。因为要快速地找到子数组的和，所以容易想到用前缀和。注意这道题因为涉及到两个长度不同的子数组 A 和 B，长度分别为 firstLen 和 secondLen，所以需要考虑 A+B 和 B+A 两种情况，谁在前都可以。

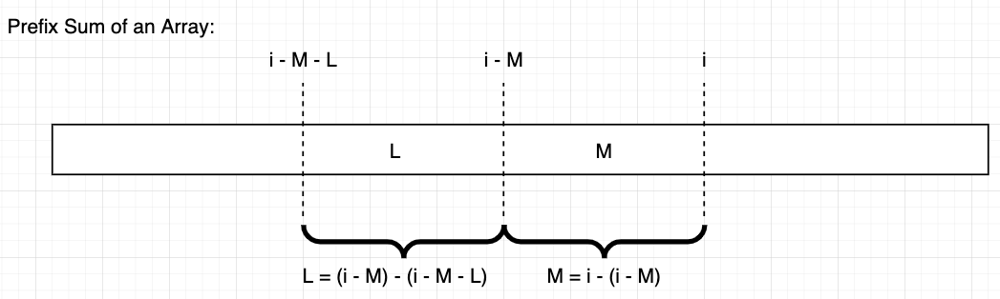
具体做法是首先我们把整个数组的前缀和计算好，用一个数组 presum 存储，这样当我们需要得到一段子数组的和的时候，我们就可以用 O(1) 的时间拿到。接着我们遍历原数组，在遍历过程中，我们用一个变量 i 表示当前遍历到哪个下标，两个子数组 A 和 B 都在下标 i 的左侧。所以当我们在某个下标 i 的时候，子数组 A 的值 = presum[i - secondLen] - presum[i - secondLen - firstLen]，子数组 B 的值 = presum[i] - presum[i - secondLen]。找到两者的最大值再相加，就是最后的结果。下面这个图可以帮助理解。

复杂度

时间O(n)
空间O(n)

代码

Java实现

class Solution {
    public int maxSumTwoNoOverlap(int[] nums, int firstLen, int secondLen) {
        int n = nums.length;
        int[] presum = new int[n + 1];
        for (int i = 0; i < n; i++) {
            presum[i + 1] = presum[i] + nums[i];
        }

        int max1 = getMax(presum, firstLen, secondLen);
        int max2 = getMax(presum, secondLen, firstLen);
        return Math.max(max1, max2);
    }

    private int getMax(int[] presum, int firstLen, int secondLen) {
		// 找到firstLen的最大值
        int maxFirst = 0;
        int max = 0;
        for (int i = firstLen + secondLen; i < presum.length; i++) {
            maxFirst = Math.max(maxFirst, presum[i - secondLen] - presum[i - secondLen - firstLen]);
			// 找到整体的最大值
            max = Math.max(max, maxFirst + presum[i] - presum[i - secondLen]);
        }
        return max;
    }
}