[LeetCode] 2316. Count Unreachable Pairs of Nodes in an Undirected Graph

You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

Return the number of pairs of different nodes that are unreachable from each other.

Example 1:

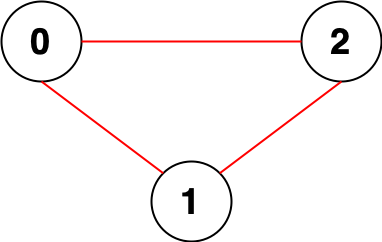
Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

Example 2:

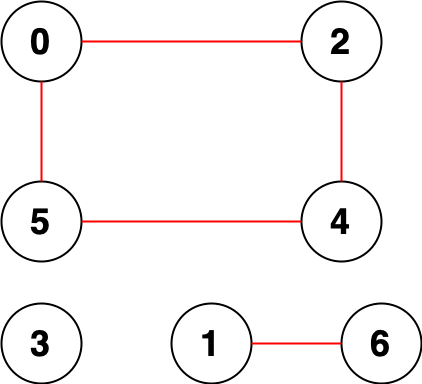
Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

Constraints:

• 1 <= n <= 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• There are no repeated edges.

统计无向图中无法互相到达点对数。

给你一个整数 n ，表示一张 无向图 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。

请你返回 无法互相到达 的不同 点对数目 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/count-unreachable-pairs-of-nodes-in-an-undirected-graph
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路是 DFS，可以参考 323题。我们把图建立起来之后，开始遍历每一个 node，遍历的同时我们记录每一个连通分量的大小。

举个例子，比如题目一共给了 n 个 node。对于当前我在遍历的某个 node，我去看一下他的所有邻居节点，这样我能计算出当前这个 node 所在的连通分量的大小，记为 connected；那么所有不在当前这个连通分量里的 node 的数量 = n - connected；那么对于当前这个连通分量里的每一个 node，他无法到达的点的个数 = n - connected；如果当前这个连通分量里有 m 个 node 的话，那么对于当前这个连通分量而言，无法互相到达的点对数量 = m * (n - connected)。

时间O(n^2) - worst case

空间O(n)

Java实现

class Solution {
    public long countPairs(int n, int[][] edges) {
        long count = 0;
        List<List<Integer>> g = buildGraph(n, edges);
        boolean[] visited = new boolean[n];

        long total = n;
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                int connected = dfs(g, visited, i, new int[1]);
                total -= connected;
                count += connected * total;
            }
        }
        return count;
    }

    private int dfs(List<List<Integer>> g, boolean[] visited, int cur, int[] count) {
        if (visited[cur]) {
            return count[0];
        }
        visited[cur] = true;
        count[0]++;
        for (int next : g.get(cur)) {
            dfs(g, visited, next, count);
        }
        return count[0];
    }

    private List<List<Integer>> buildGraph(int n, int[][] edges) {
        List<List<Integer>> g = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            g.add(new ArrayList<>());
        }
        for (int[] e : edges) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }
        return g;
    }
}

 

LeetCode 题目总结