[LeetCode] 1326. Minimum Number of Taps to Open to Water a Garden

There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).

There are n + 1 taps located at points [0, 1, ..., n] in the garden.

Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.

Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

Example 1:

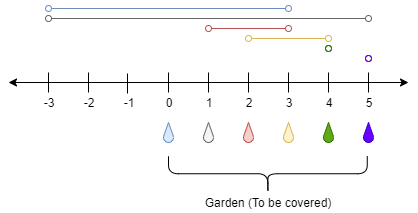
Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]

Example 2:

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.

Constraints:

• 1 <= n <= 104
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

灌溉花园的最少水龙头数目。

在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, ..., n] 。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i -  ranges[i], i + ranges[i]] 。

请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方，请你返回 -1 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-number-of-taps-to-open-to-water-a-garden
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这道题有多种解法，这里我提供一个扫描线的思路。

这道题给了若干个水龙头，问最少需要多少个水龙头才能确保所有范围都能被浇水，所以这里我对 input 数据做了一点处理。ranges 数组表示的是每个水龙头的覆盖范围，我把 ranges 变为一个二维数组，表示每个水龙头能覆盖的左边界和右边界，记为 region。接着我对 region 排序，排序的规则是左边界更小的在前，如果左边界一样，那么右边界小的在前。

排序之后我们需要几个变量，res 记录最后需要几个水龙头，right 记录当前水龙头能覆盖到的右边界的下标，cur 记录的是当前遍历到第几个水龙头了。其余部分参见代码注释。

时间O(nlogn)

空间O(n)

Java实现

class Solution {
    public int minTaps(int n, int[] ranges) {
        // 二维数组记录每个水龙头能覆盖的范围
        int[][] region = new int[n + 1][2];
        for (int i = 0; i <= n; i++) {
            int[] temp = new int[2];
            temp[0] = Math.max(0, i - ranges[i]);
            temp[1] = Math.min(n, i + ranges[i]);
            region[i] = temp;
        }
        Arrays.sort(region, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);

        int res = 0;
        int right = 0;
        int cur = 0;
        while (cur < n + 1) {
            // 当前区间无法覆盖到最右的有效工作范围，那么就会存在覆盖不到的间隙
            if (region[cur][0] > right) {
                break;
            }
            int rt = right;
            while (cur < n + 1 && region[cur][0] <= right) {
                rt = Math.max(rt, region[cur][1]);
                cur++;
            }
            res++;
            right = rt;
            if (right == n) {
                break;
            }
        }
        return right == n ? res : -1;
    }
}

 

LeetCode 题目总结