[LeetCode] 790. Domino and Tromino Tiling

You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.

Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 109 + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

 

Example 1:

Input: n = 3
Output: 5
Explanation: The five different ways are show above.

Example 2:

Input: n = 1
Output: 1

Constraints:

• 1 <= n <= 1000

多米诺和托米诺平铺。

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 "L" 的托米诺形。两种形状都可以旋转。

给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/domino-and-tromino-tiling
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路是动态规划。我参考了这个帖子，写的很好，图示可以清楚说明推导的过程。经过推导，我们发现，除了 f(1) 和 f(2) 之外，后面的 f(n) 都是可以通过前面更小的函数结果组合而成的。

 

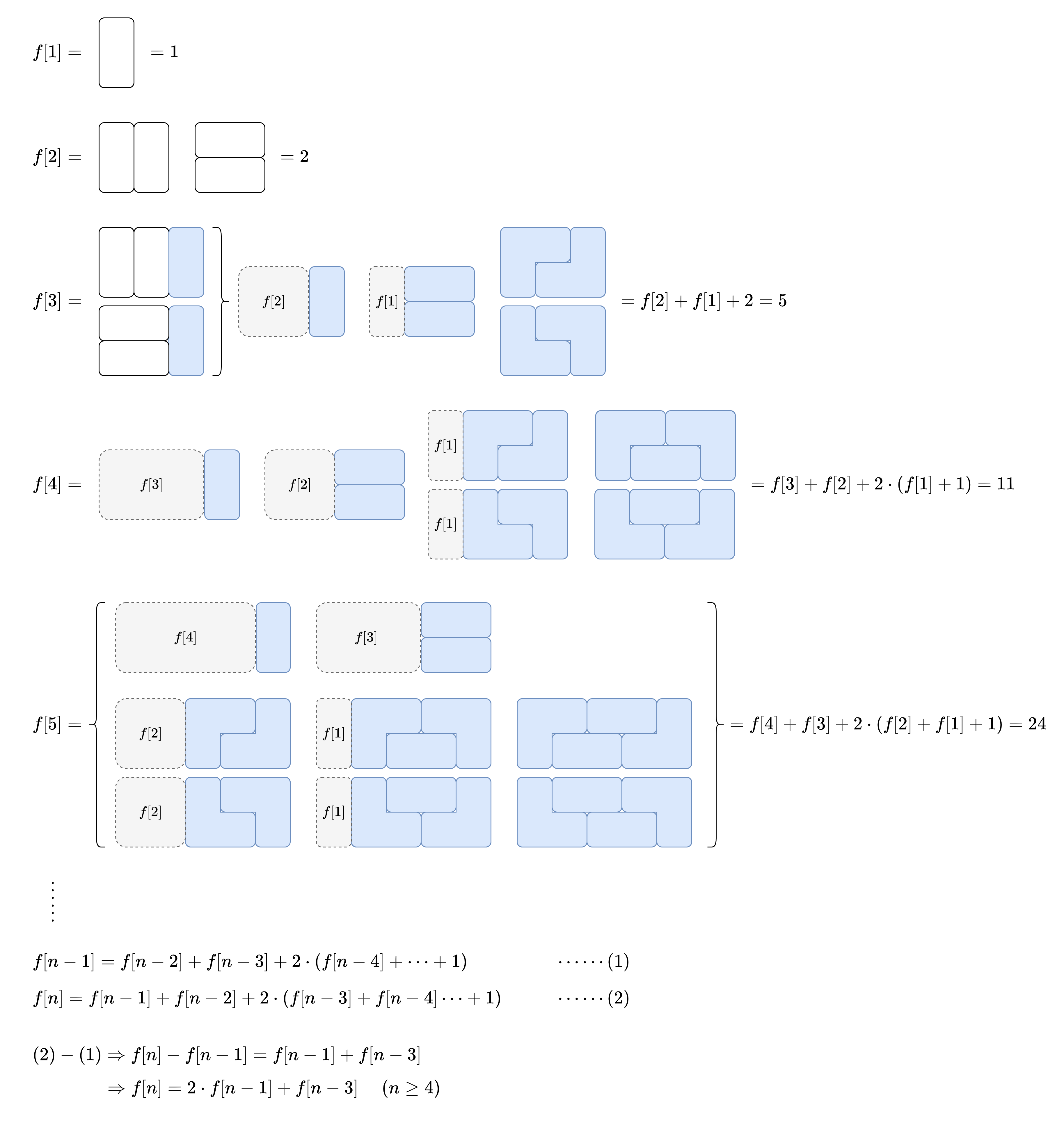
时间O(n)

空间O(n) - dp数组

Java实现

class Solution {
    private int MOD = (int) Math.pow(10, 9) + 7;

    public int numTilings(int n) {
        if (n == 1) {
            return 1;
        }
        long[] f = new long[n + 1];
        f[0] = 1;
        f[1] = 1;
        f[2] = 2;
        for (int i = 3; i <= n; i++) {
            f[i] = (f[i - 1] * 2 + f[i - 3]) % MOD;
        }
        return (int) f[n];
    }
}

 

LeetCode 题目总结