[LeetCode] 1971. Find if Path Exists in Graph

There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from vertex source to vertex destination.

Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.

Example 1:

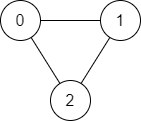
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

Example 2:

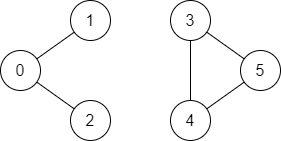
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

Constraints:

• 1 <= n <= 2 * 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ui, vi <= n - 1
• ui != vi
• 0 <= source, destination <= n - 1
• There are no duplicate edges.
• There are no self edges.

寻找图中是否存在路径。

有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的 有效路径 。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在 有效路径 ，则返回 true，否则返回 false 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/find-if-path-exists-in-graph
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这是一道图论的题目，这里我给出三种思路，分别是BFS，DFS 和 并查集。题意很好理解，给了一些定点，其中包含 source 和 destination，请问 source 和 destination 是否连通。

BFS - 需要额外的 boolean 数组记录每个 node 是否被访问过，避免死循环

时间O(n)

空间O(n)

Java实现

class Solution {
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        List<List<Integer>> g = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            g.add(new ArrayList<>());
        }
        
        for (int[] e : edges) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }
        
        boolean[] visited = new boolean[n];
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(source);
        while (!queue.isEmpty()) {
            int cur = queue.poll();
            if (cur == destination) {
                return true;
            }
            visited[cur] = true;
            int size = g.get(cur).size();
            for (int i = 0; i < size; i++) {
                int next = g.get(cur).get(i);
                if (visited[next] == false) {
                    queue.offer(next);
                }
            }
        }
        return false;
    }
}

 

DFS - 也需要额外的 boolean 数组记录每个 node 是否被访问过，避免死循环

时间O(n)

空间O(n)

Java实现

class Solution {
    private boolean[] visited;
    private List<List<Integer>> g;

    public boolean validPath(int n, int[][] edges, int source, int destination) {
        visited = new boolean[n];
        g = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            g.add(new ArrayList<>());
        }
        for (int[] e : edges) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }
        return dfs(source, destination);
    }

    private boolean dfs(int source, int destination) {
        if (source == destination) {
            return true;
        }
        visited[source] = true;
        for (int next : g.get(source)) {
            if (!visited[next] && dfs(next, destination)) {
                return true;
            }
        }
        return false;
    }
}

 

Union Find - P 数组记录的是每个 node 的父节点，最后判断 source 和 destination 的父节点是否相同

时间O(V + E)

空间O(V + E)

Java实现

class Solution {
    private int[] p;

    public boolean validPath(int n, int[][] edges, int source, int destination) {
        p = new int[n];
        for (int i = 0; i < n; i++) {
            p[i] = i;
        }
        for (int[] e : edges) {
            p[find(e[0])] = find(e[1]);
        }
        return find(source) == find(destination);
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

 

LeetCode 题目总结