[LeetCode] 416. Partition Equal Subset Sum

Given a non-empty array nums containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.

Example 1:

Input: nums = [1,5,11,5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].

Example 2:

Input: nums = [1,2,3,5]
Output: false
Explanation: The array cannot be partitioned into equal sum subsets.

Constraints:

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

分割等和子集。

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/partition-equal-subset-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这是一道非常好的动态规划/0-1背包问题。为什么是0-1背包是因为每个数字只能用一次，只能选择用或不用。

首先我们来理解一下题意，题目给了一个非空的正整数数组（nums[i] > 0），请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。这个问题我们可以把他转化为我们能不能从中挑出一些数字，使得这些数字的和正好为所有数字的和的一半。

这里我们创建一个二维的DP数组，定义是从前 i 个数字内选取若干个正整数，是否存在一种方案使得他们的和等于 j。其他讲解可以直接参见代码注释。

时间O(mn)

空间O(mn)

Java实现

class Solution {
    public boolean canPartition(int[] nums) {
        int len = nums.length;
        int sum = 0;
        int max = 0;
        for (int num : nums) {
            sum += num;
            max = Math.max(max, num);
        }
        int target = sum / 2;

        // corner case
        if (sum % 2 == 1) {
            return false;
        }
        if (max > target) {
            return false;
        }

        // normal case
        // dp定义是从数组的前 i 个数内选取若干个正整数，是否存在一种方案使得他们的和等于 j
        boolean[][] dp = new boolean[len][target + 1];
        // 因为input都是正数，所以无法使得他们的和等于0
        dp[0][0] = false;
        // 任何方案，只要不选，都可以使他们的和为0
        for (int i = 0; i < len; i++) {
            dp[i][0] = true;
        }
        // 选了第一个数字，和为nums[0]
        dp[0][nums[0]] = true;
        for (int i = 1; i < len; i++) {
            for (int j = 1; j < target + 1; j++) {
                // 不考虑当前数字
                dp[i][j] = dp[i - 1][j];
                if (j >= nums[i]) {
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
                }
            }
            // 剪枝
            if (dp[i][target] == true) {
                return true;
            }
        }
        return dp[len - 1][target];
    }
}

 

我们注意到DP数组的更新其实每次都只跟上一行的DP值有关，所以我们这里考虑把二维数组降成一维。注意27行为什么 j 指针是从右往左扫描，因为这样我们就不会覆盖掉之前记录的DP值了。

时间O(mn)

空间O(n)

Java实现

class Solution {
    public boolean canPartition(int[] nums) {
        int len = nums.length;
        int sum = 0;
        int max = 0;
        for (int num : nums) {
            sum += num;
            max = Math.max(max, num);
        }
        int target = sum / 2;

        // corner case
        if (sum % 2 == 1) {
            return false;
        }
        if (max > target) {
            return false;
        }

        // normal case
        boolean[] dp = new boolean[target + 1];
        dp[0] = true;
        if (nums[0] <= target) {
            dp[nums[0]] = true;
        }
        for (int i = 1; i < nums.length; i++) {
            for (int j = target; j >= nums[i]; j--) {
                if (dp[target]) {
                    return true;
                }
                dp[j] = dp[j] || dp[j - nums[i]];
            }
        }
        return dp[target];
    }
}

 

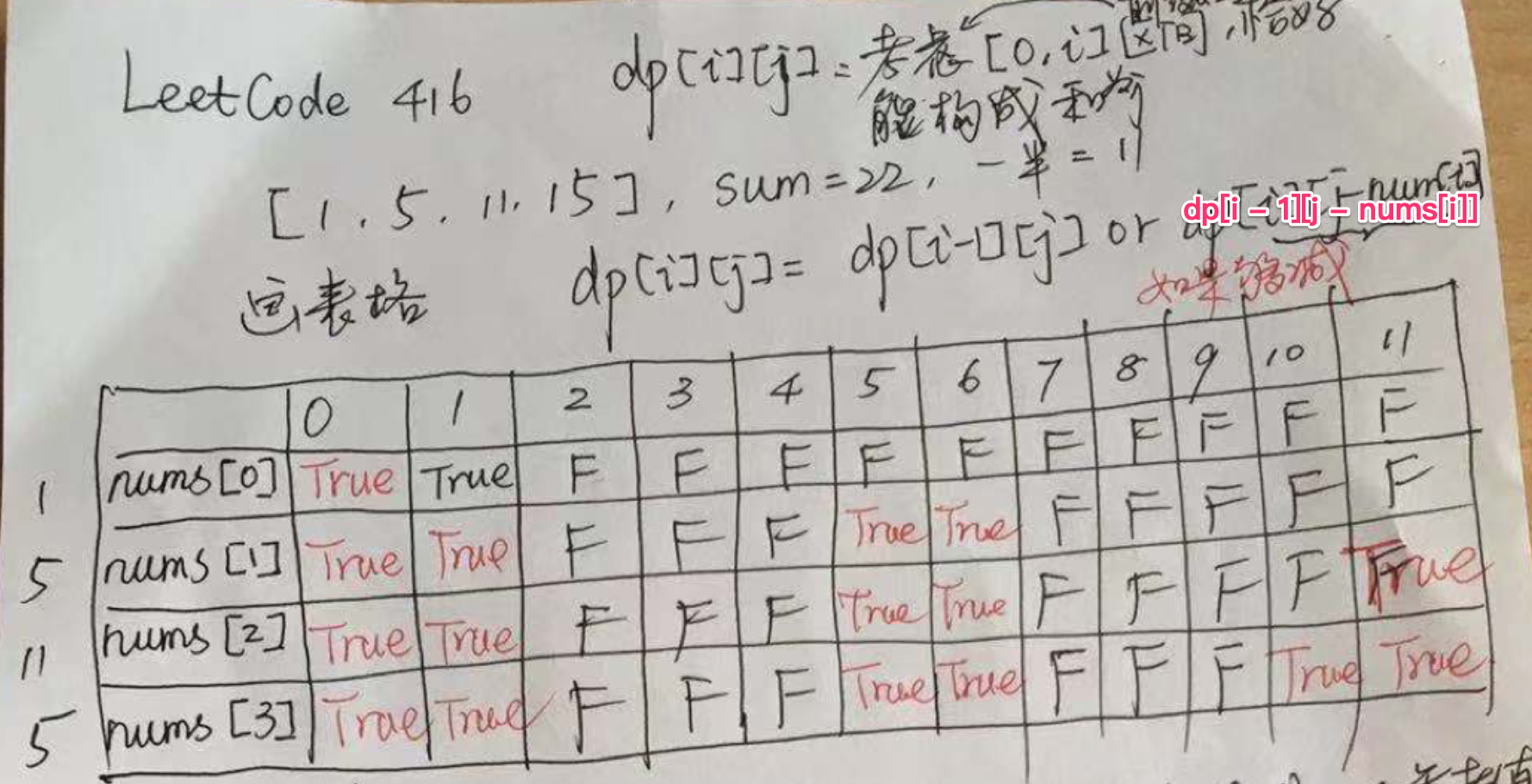
最后我再补充一下这道题的 DP 数组如何填表的问题。我引用了这个帖子里的表。因为每个数字只能用一次，所以这张表是一行一行填写的。表格的第一行 0 - 11 表示的是数组和 sum。表格中第一列 sum == 0 他这里都填了 true（所有红色的true），这里有待商榷但是不影响最终结果。

第一行 nums[0] 那一行，如果选择了 nums[0]，那么我们可以构造一个子数组使得他的和 = 1，所以在 [1, 1] 那个位置可以填 true。这一行剩下的部分，因为 1 已经选择过了同时无论选不选1，都无法构造成一个更大的 sum，所以 nums[0] 那一行后面全是 false。

第二行 nums[1] 那一行，1 的位置可以继承上一行来的结果，因为在这里我们可以不选择 nums[1]，一样可以构造一个数组和 == 1 的子数组。后面 5 的部分为什么可以填 true 是因为直接加5就可以使 sum = 5，同时 6 也是 true 是因为 dp[i - 1][6 - 5] == dp[i - 1][1] == true，所以这里可以继承过来。

之后的部分都类推，需要结合代码理解填表的过程。

LeetCode 题目总结