[LeetCode] 1995. Count Special Quadruplets

Given a 0-indexed integer array nums, return the number of distinct quadruplets (a, b, c, d) such that:

• nums[a] + nums[b] + nums[c] == nums[d], and
• a < b < c < d

Example 1:

Input: nums = [1,2,3,6]
Output: 1
Explanation: The only quadruplet that satisfies the requirement is (0, 1, 2, 3) because 1 + 2 + 3 == 6.

Example 2:

Input: nums = [3,3,6,4,5]
Output: 0
Explanation: There are no such quadruplets in [3,3,6,4,5].

Example 3:

Input: nums = [1,1,1,3,5]
Output: 4
Explanation: The 4 quadruplets that satisfy the requirement are:
- (0, 1, 2, 3): 1 + 1 + 1 == 3
- (0, 1, 3, 4): 1 + 1 + 3 == 5
- (0, 2, 3, 4): 1 + 1 + 3 == 5
- (1, 2, 3, 4): 1 + 1 + 3 == 5

Constraints:

• 4 <= nums.length <= 50
• 1 <= nums[i] <= 100

统计特殊四元组。

给你一个 下标从 0 开始 的整数数组 nums ，返回满足下述条件的 不同 四元组 (a, b, c, d) 的 数目 ：

nums[a] + nums[b] + nums[c] == nums[d] ，且
a < b < c < d

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/count-special-quadruplets
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这道题也属于 X sum 那一类的题。暴力解不难想到，就是用4个指针分别去遍历题目中的 a, b, c, d 四个下标。然而这道题的最优解是 O(n^2)。

因为题目有对下标做要求，所以这道题是不能排序的。

• a < b < c < d

题目要我们找的是满足这个公式的四元组，nums[a] + nums[b] + nums[c] == nums[d] 且 a < b < c < d。我们可以把这个等式变成 nums[a] + nums[b] = nums[d] - nums[c]，然后用 hashmap 去记录所有 unique 的 nums[d] - nums[c]。既然时间复杂度降了，那么势必会有空间上的牺牲，以空间换时间。

至于具体做法上，需要有一些技巧。这里我们用一个 for 循环去遍历 b 的下标，对于每一个 b 的下标，我们可以找到 c 和 d 的下标的范围（肯定在 b 的右侧，其中 c = b + 1）。参考下面这个截图（引用）。

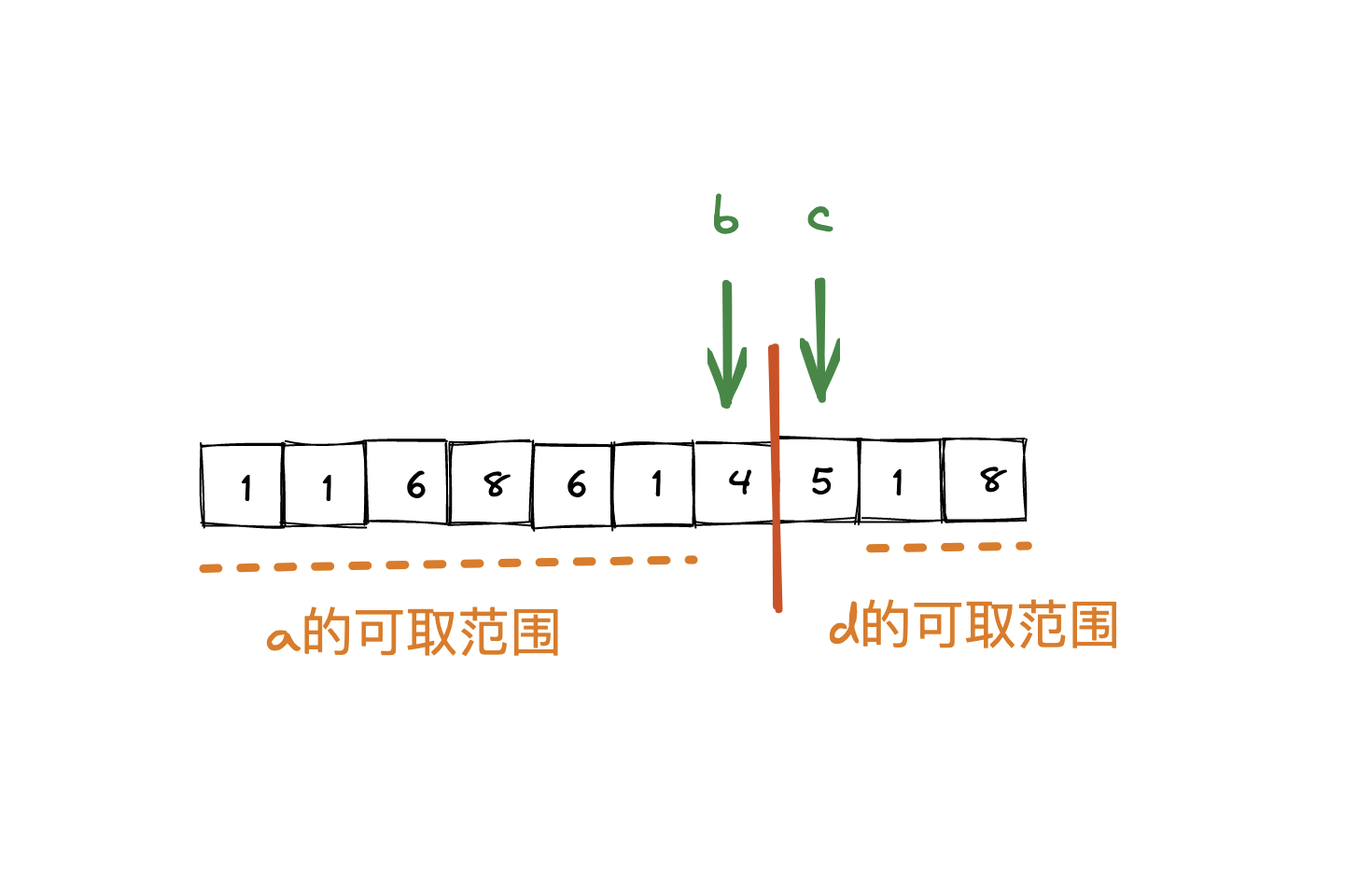
当 b 的位置固定的时候，我们定义 c = b + 1，然后用另一个指针去遍历所有的 d，这样我们就能得到所有 d - c 的组合。而且随着 b 不断往左移动，我们对 c 的取值范围也是不断变大的，最终我们会得到所有 d - c 的组合。此时我们再用第二个 for 循环，得到所有 a + b 的组合，看看hashmap中是否已经存在，若存在，则说明我们找到了一个组合满足 nums[a] + nums[b] = nums[d] - nums[c]。

时间O(n^2)

空间O(n)

Java实现

class Solution {
    public int countQuadruplets(int[] nums) {
        int len = nums.length;
        int res = 0;
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int b = len - 3; b >= 1; b--) {
            for (int d = b + 2; d < len; d++) {
                map.put(nums[d] - nums[b + 1], map.getOrDefault(nums[d] - nums[b + 1], 0) + 1);
            }
            for (int a = 0; a < b; a++) {
                res += map.getOrDefault(nums[a] + nums[b], 0);
            }
        }
        return res;
    }
}

 

two sum题目总结

LeetCode 题目总结