[LeetCode] 1245. Tree Diameter

The diameter of a tree is the number of edges in the longest path in that tree.

There is an undirected tree of n nodes labeled from 0 to n - 1. You are given a 2D array edges where edges.length == n - 1 and edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the tree.

Return the diameter of the tree.

Example 1:

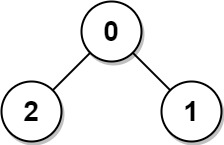
Input: edges = [[0,1],[0,2]]
Output: 2
Explanation: The longest path of the tree is the path 1 - 0 - 2.

Example 2:

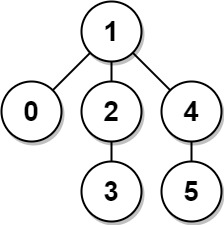
Input: edges = [[0,1],[1,2],[2,3],[1,4],[4,5]]
Output: 4
Explanation: The longest path of the tree is the path 3 - 2 - 1 - 4 - 5.

Constraints:

• n == edges.length + 1
• 1 <= n <= 104
• 0 <= ai, bi < n
• ai != bi

树的直径。

给你这棵「无向树」，请你测算并返回它的「直径」：这棵树上最长简单路径的 边数。

我们用一个由所有「边」组成的数组 edges 来表示一棵无向树，其中 edges[i] = [u, v] 表示节点 u 和 v 之间的双向边。

树上的节点都已经用 {0, 1, ..., edges.length} 中的数做了标记，每个节点上的标记都是独一无二的。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/tree-diameter
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

虽然题目描述是一棵树，其实这是一道图论的题目，我给出一个 DFS 的思路。首先我们还是建图，图建立好之后，我们用一个 helper 函数进行 DFS 遍历。对于当前某个节点的所有邻居，我们对邻居再做DFS遍历并对长度 + 1。这里我们需要利用到类似543题的思路，对于同一个 node 延伸出去的长度，由于我们不知道遍历的方向，所以我们记录 max1 和 max2，表示经过某个节点能组成的最大的长度和次大的长度。DFS 函数在返回的时候，依然返回最长的长度 max1 但是对于全局变量 res 的更新，是 res = Math.max(res, max1 + max2)。因为 res 本质上记录的是经过当前节点的 diameter，而 DFS 往上一层返回的值相当于是父节点要知道到底哪个孩子返回的路径是最长的。

时间O(n)

空间O(n)

Java实现

class Solution {
    int res = 0;

    public int treeDiameter(int[][] edges) {
        List<Integer>[] graph = new List[edges.length + 1];
        for (int i = 0; i < graph.length; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] e : edges) {
            graph[e[0]].add(e[1]);
            graph[e[1]].add(e[0]);
        }
        dfs(graph, 0, -1);
        return res;
    }

    private int dfs(List<Integer>[] graph, int cur, int prev) {
        List<Integer> list = graph[cur];
        int max1 = 0;
        int max2 = 0;
        // 遍历每个邻居节点
        for (int nei : list) {
            // 防止走回头路
            if (nei != prev) {
                int max = dfs(graph, nei, cur) + 1;
                if (max >= max1) {
                    max2 = max1;
                    max1 = max;
                } else if (max >= max2) {
                    max2 = max;
                }
                // res记录的是经过当前节点最长的diameter是多少
                // 但是DFS函数返回的是当前节点能找到的最长的长度，把这个信息返回给父节点
                res = Math.max(res, max1 + max2);
            }
        }
        return max1;
    }
}

 

相关题目

543. Diameter of Binary Tree

1245. Tree Diameter

2246. Longest Path With Different Adjacent Characters

LeetCode 题目总结