[LeetCode] 261. Graph Valid Tree

You have a graph of n nodes labeled from 0 to n - 1. You are given an integer n and a list of edges where edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the graph.

Return true if the edges of the given graph make up a valid tree, and false otherwise.

Example 1:

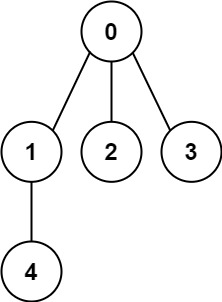
Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true

Example 2:

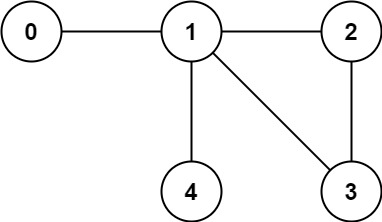
Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false

Constraints:

• 1 <= n <= 2000
• 0 <= edges.length <= 5000
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• There are no self-loops or repeated edges.

以图判树。

给定从 0 到 n-1 标号的 n 个结点，和一个无向边列表（每条边以结点对来表示），请编写一个函数用来判断这些边是否能够形成一个合法有效的树结构。

注意：你可以假定边列表 edges 中不会出现重复的边。由于所有的边是无向边，边 [0,1] 和边 [1,0] 是相同的，因此不会同时出现在边列表 edges 中。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/graph-valid-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这道题属于图和树的综合题。给的 input 是节点的个数 n 和一些边 edges，请你判断能否组成一棵树。有一个概念需要复习，树和图的区别在于图是可以有环 (cycle) 的，树不能有环；同时图的节点有可能不会连在一片，但是树的所有节点必定都是相连成一片的。对于这道题，有一些 corner case 需要特判，如果只有一个节点的话，那么就一定没有 edges；因为题设说了不会给额外的边，所以如果边的数量 != 节点数量 - 1的话，一定不是树。

照着这个思路，我还是提供三种做法，BFS, DFS 和 Union Find。三种做法的时间空间复杂度都一样，union find 在运行时间上可以通过路径压缩变得更快。判断的逻辑是如果反复遇到某个节点或者最终有某个节点没有访问过，就说明有环或者是图（比如有超过一组联通的点）

BFS

时间O(V * E)

空间O(n)

Java实现

class Solution {
    public boolean validTree(int n, int[][] edges) {
        // create graph
        List<List<Integer>> graph = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            graph.add(new ArrayList<>());
        }
        for (int i = 0; i < edges.length; i++) {
            graph.get(edges[i][0]).add(edges[i][1]);
            graph.get(edges[i][1]).add(edges[i][0]);
        }

        boolean[] visited = new boolean[n];
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(0);
        while (!queue.isEmpty()) {
            int cur = queue.poll();
            if (visited[cur] == true) {
                return false;
            }
            visited[cur] = true;
            for (int nei : graph.get(cur)) {
                if (!visited[nei]) {
                    queue.offer(nei);
                }
            }
        }

        for (int i = 0; i < n; i++) {
            if (visited[i] == false) {
                return false;
            }
        }
        return true;
    }
}

 

DFS

时间O(V * E)

空间O(n)

Java实现

class Solution {
    public boolean validTree(int n, int[][] edges) {
        // create graph
        List<List<Integer>> g = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            g.add(new ArrayList<>());
        }
        for (int[] e : edges) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }

        HashSet<Integer> visited = new HashSet<>();
        visited.add(0);
        boolean res = helper(g, visited, 0, -1);
        if (res == false) {
            return false;
        }
        return visited.size() == n ? true : false;
    }

    private boolean helper(List<List<Integer>> g, HashSet<Integer> visited, int cur, int parent) {
        List<Integer> neighbors = g.get(cur);
        for (int nei : neighbors) {
            if (nei == parent) {
                continue;
            }
            // cycle
            if (visited.contains(nei)) {
                return false;
            }
            visited.add(nei);
            boolean res = helper(g, visited, nei, cur);
            if (res == false) {
                return false;
            }
        }
        return true;
    }
}

 

Union Find

时间O(V * E)

空间O(n)

Java实现

class Solution {
    public boolean validTree(int n, int[][] edges) {
        // corner case
        if (n == 1 && edges.length == 0) {
            return true;
        }
        if (n < 1 || edges == null || edges.length != n - 1) {
            return false;
        }

        // normal case
        int[] roots = new int[n];
        for (int i = 0; i < n; i++) {
            roots[i] = -1;
        }

        for (int[] pair : edges) {
            int x = find(roots, pair[0]);
            int y = find(roots, pair[1]);
            if (x == y) {
                return false;
            }
            roots[x] = y;
        }
        return true;
    }

    private int find(int[] roots, int i) {
        while (roots[i] != -1) {
            i = roots[i];
        }
        return i;
    }
}

 

相关题目

261. Graph Valid Tree

323. Number of Connected Components in an Undirected Graph

547. Friend Circles

LeetCode 题目总结