[LeetCode] 323. Number of Connected Components in an Undirected Graph

 

You have a graph of n nodes. You are given an integer n and an array edges where edges[i] = [ai, bi] indicates that there is an edge between ai and bi in the graph.

Return the number of connected components in the graph.

Example 1:

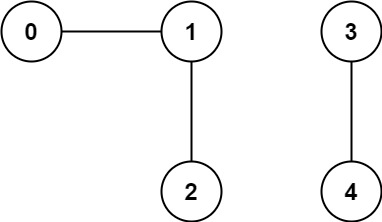
Input: n = 5, edges = [[0,1],[1,2],[3,4]]
Output: 2

Example 2:

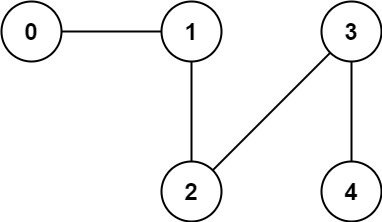
Input: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]]
Output: 1

 

Constraints:

• 1 <= n <= 2000
• 1 <= edges.length <= 5000
• edges[i].length == 2
• 0 <= ai <= bi < n
• ai != bi
• There are no repeated edges.

无向图中连通分量的数目。

你有一个包含 n 个节点的图。给定一个整数 n 和一个数组 edges ，其中 edges[i] = [ai, bi] 表示图中 ai 和 bi 之间有一条边。

返回 图中已连接分量的数目 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/number-of-connected-components-in-an-undirected-graph
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这道题可以归结为flood fill类型的题，我这里给出三种解法，分别是 BFS, DFS 和并查集 union find。其中 DFS 和并查集是需要重点掌握的，BFS 的复杂度略高。

BFS

时间O(n^2)

空间O(n)

Java实现

class Solution {
    public int countComponents(int n, int[][] edges) {
        int count = 0;
        List<List<Integer>> g = new ArrayList<>();
        boolean[] visited = new boolean[n];
        for (int i = 0; i < n; i++) {
            g.add(new ArrayList<>());
        }
        for (int[] e : edges) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }

        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                count++;
                Queue<Integer> queue = new LinkedList<>();
                queue.offer(i);
                while (!queue.isEmpty()) {
                    int index = queue.poll();
                    visited[index] = true;
                    for (int next : g.get(index)) {
                        if (!visited[next]) {
                            queue.offer(next);
                        }
                    }
                }
            }
        }
        return count;
    }
}

 

DFS

时间O(n^2)

空间O(n)

Java实现

class Solution {
    public int countComponents(int n, int[][] edges) {
        int count = 0;
        List<List<Integer>> g = new ArrayList<>();
        boolean[] visited = new boolean[n];
        for (int i = 0; i < n; i++) {
            g.add(new ArrayList<>());
        }
        for (int[] e : edges) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }

        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                count++;
                dfs(visited, i, g);
            }
        }
        return count;
    }

    private void dfs(boolean[] visited, int node, List<List<Integer>> g) {
        visited[node] = true;
        for (int next : g.get(node)) {
            if (!visited[next]) {
                dfs(visited, next, g);
            }
        }
    }
}

 

Union Find

时间O(V * E)

空间O(n)

Java实现

class Solution {
    public int countComponents(int n, int[][] edges) {
        int count = n;
        int[] parents = new int[n];
        for (int i = 0; i < n; i++) {
            parents[i] = i;
        }
        for (int[] edge : edges) {
            int p = find(parents, edge[0]);
            int q = find(parents, edge[1]);
            if (p != q) {
                parents[p] = q;
                count--;
            }
        }
        return count;
    }

    private int find(int[] parents, int i) {
        while (parents[i] != i) {
            parents[i] = parents[parents[i]]; // 路径压缩
            i = parents[i];
        }
        return i;
    }
}

 

相关题目

261. Graph Valid Tree

323. Number of Connected Components in an Undirected Graph

547. Friend Circles

LeetCode 题目总结