[LeetCode] 1586. Binary Search Tree Iterator II

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):

• BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
• boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
• int next() Moves the pointer to the right, then returns the number at the pointer.
• boolean hasPrev() Returns true if there exists a number in the traversal to the left of the pointer, otherwise returns false.
• int prev() Moves the pointer to the left, then returns the number at the pointer.

Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() and prev() calls will always be valid. That is, there will be at least a next/previous number in the in-order traversal when next()/prev() is called.

Follow up: Could you solve the problem without precalculating the values of the tree?

Example 1:

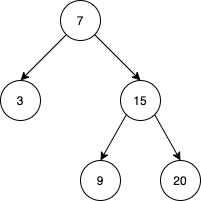
Input
["BSTIterator", "next", "next", "prev", "next", "hasNext", "next", "next", "next", "hasNext", "hasPrev", "prev", "prev"]
[[[7, 3, 15, null, null, 9, 20]], [null], [null], [null], [null], [null], [null], [null], [null], [null], [null], [null], [null]]
Output
[null, 3, 7, 3, 7, true, 9, 15, 20, false, true, 15, 9]

Explanation
// The underlined element is where the pointer currently is.
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]); // state is  [3, 7, 9, 15, 20]
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 3
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 7
bSTIterator.prev(); // state becomes [3, 7, 9, 15, 20], return 3
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 7
bSTIterator.hasNext(); // return true
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 9
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 15
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 20
bSTIterator.hasNext(); // return false
bSTIterator.hasPrev(); // return true
bSTIterator.prev(); // state becomes [3, 7, 9, 15, 20], return 15
bSTIterator.prev(); // state becomes [3, 7, 9, 15, 20], return 9

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 0 <= Node.val <= 106
• At most 105 calls will be made to hasNext, next, hasPrev, and prev.

二叉搜索树迭代器II。

实现二叉搜索树（BST）的中序遍历迭代器 BSTIterator 类：

BSTIterator(TreeNode root) 初始化 BSTIterator 类的实例。二叉搜索树的根节点 root 作为构造函数的参数传入。内部指针使用一个不存在于树中且小于树中任意值的数值来初始化。
boolean hasNext() 如果当前指针在中序遍历序列中，存在右侧数值，返回 true ，否则返回 false 。
int next() 将指针在中序遍历序列中向右移动，然后返回移动后指针所指数值。
boolean hasPrev() 如果当前指针在中序遍历序列中，存在左侧数值，返回 true ，否则返回 false 。
int prev() 将指针在中序遍历序列中向左移动，然后返回移动后指针所指数值。
注意，虽然我们使用树中不存在的最小值来初始化内部指针，第一次调用 next() 需要返回二叉搜索树中最小的元素。

你可以假设 next() 和 prev() 的调用总是有效的。即，当 next()/prev() 被调用的时候，在中序遍历序列中一定存在下一个/上一个元素。

进阶：你可以不提前遍历树中的值来解决问题吗？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-search-tree-iterator-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目是173题的版本二，题设差不多，也是遍历BST，但是本题需要额外输出一个prev，既中序遍历的前一个节点。同时本题的 followup 是问你能否不提前遍历树中的值来解决问题。

既然是遍历二叉搜索树那么一定还是逃不掉中序遍历的思想。但是这道题的 followup 是问能否不提前遍历，所以我们可以一边遍历一边得出需要的值，同时用一个 list 存住已经遍历过的值。具体的做法是，首先先按照中序遍历的前半段，不断地把当前节点入栈，并一直往左子树走，直到走到最小的左子节点位为止。

hasNext() 函数问的是当前节点之后是否还有节点，我们一般判断的逻辑是 stack 是否为空，但是本题我们可以先判断下一个节点是否已经被存储在 list 中了（因为题目会反复问你 prev 和 next 是否存在），如果不在，再判断 stack 是否为空。

next() 函数，如果 list 中存在 index + 1，则输出这个节点值；如果如果 list 中不存在 index + 1，但是 hasNext() 为true的话，就说明下一个节点还未从 stack 中弹出，我们把它从 stack 中弹出并且加入 list。记得index++。

hasPrev() 和 prev() 就比较简单了，因为是往前看，所以直接去判断 inRange 是否合法和去 list 里面找相应 index 即可。

时间O(n)

空间O(n)

Java实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class BSTIterator {
    Stack<TreeNode> stack = new Stack<>();
    List<TreeNode> list = new ArrayList<>();
    int index = -1;

    private void pushLeft(TreeNode root) {
        while (root != null) {
            stack.push(root);
            root = root.left;
        }
    }

    private boolean inRange(int i) {
        return i >= 0 && i < list.size();
    }

    public BSTIterator(TreeNode root) {
        pushLeft(root);
    }

    public boolean hasNext() {
        if (inRange(index + 1)) {
            return true;
        }
        return !stack.isEmpty();
    }

    public int next() {
        int nextVal = 0;
        if (inRange(index + 1)) {
            nextVal = list.get(index + 1).val;
        } else {
            TreeNode next = stack.pop();
            pushLeft(next.right);
            list.add(next);
            nextVal = next.val;
        }
        index++;
        return nextVal;
    }

    public boolean hasPrev() {
        return inRange(index - 1);
    }

    public int prev() {
        return list.get(--index).val;
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator obj = new BSTIterator(root);
 * boolean param_1 = obj.hasNext();
 * int param_2 = obj.next();
 * boolean param_3 = obj.hasPrev();
 * int param_4 = obj.prev();
 */

 

相关题目

173. Binary Search Tree Iterator

1586. Binary Search Tree Iterator II

LeetCode 题目总结