[LeetCode] 510. Inorder Successor in BST II

Given a node in a binary search tree, find the in-order successor of that node in the BST.

If that node has no in-order successor, return null.

The successor of a node is the node with the smallest key greater than node.val.

You will have direct access to the node but not to the root of the tree. Each node will have a reference to its parent node. Below is the definition for Node:

class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

Follow up:

Could you solve it without looking up any of the node's values?

Example 1:

Input: tree = [2,1,3], node = 1
Output: 2
Explanation: 1's in-order successor node is 2. Note that both the node and the return 
value is of Node type.

Example 2:

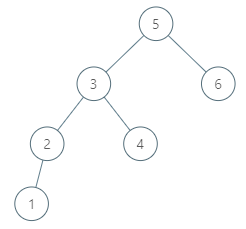
Input: tree = [5,3,6,2,4,null,null,1], node = 6
Output: null
Explanation: There is no in-order successor of the current node, so the answer is null.

Example 3:

Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], 
node = 15
Output: 17

Example 4:

Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], 
node = 13
Output: 15

Example 5:

Input: tree = [0], node = 0
Output: null

Constraints:

• -10^5 <= Node.val <= 10^5
• 1 <= Number of Nodes <= 10^4
• All Nodes will have unique values.

二叉搜索树中的中序后继 II。

这道题是285题的延续，但是题设稍微有些变化。这道题给的是一个随机的节点 node，不给你根节点了；给你这个节点 node 的同时，可以允许你访问这个节点的 val，左孩子，右孩子和父亲节点。依然是请你返回这个节点的中序后继。

思路分两部分，如果这个节点自己有右子树怎么办，和如果这个节点没有右子树怎么办。第一种情况，如果 node 有右子树，那么要找的节点是其右子树里面最小的左孩子。

第二种情况，如果 node 没有右子树，那么要找的中序后继基本上就是在找这个节点的某个父亲节点。但是这里面又分两种子情况，一种是如果我是一个左子树，我要找的很显然是我的最直接的父亲节点，比如例子4里面的2，我找的应该是3，3就是2的父亲节点。还有一种情况是比如我是4（例子2），我是左子树的最右孩子，我的中序遍历的后继节点是根节点5，我不光要试图往父亲节点跑，同时我还需要判断，我每往上走一步的时候，我到达的这个节点的右孩子到底是不是我自己，否则就会和第一种子情况一样，没法区分开了。

时间O(n)

空间O(1)

Java实现

class Solution {
    public Node inorderSuccessor(Node node) {
        // corner case
        if (node == null) {
            return null;
        }
        // if right tree is not empty
        // find the most left node on this right tree
        if (node.right != null) {
            Node suc = node.right;
            while (suc.left != null) {
                suc = suc.left;
            }
            return suc;
        }

        // if right tree is empty
        while (node.parent != null && node.parent.right == node) {
            node = node.parent;
        }
        return node.parent;
    }
}

 

相关题目

285. Inorder Successor in BST

510. Inorder Successor in BST II

LeetCode 题目总结