[LeetCode] 1059. All Paths from Source Lead to Destination

Given the edges of a directed graph, and two nodes source and destination of this graph, determine whether or not all paths starting from source eventually end at destination, that is:

• At least one path exists from the source node to the destination node
• If a path exists from the source node to a node with no outgoing edges, then that node is equal to destination.
• The number of possible paths from source to destination is a finite number.

Return true if and only if all roads from source lead to destination.

Example 1:

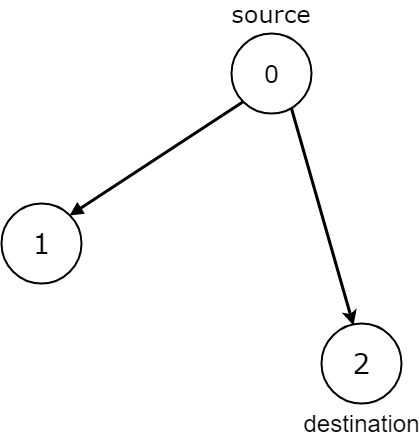
Input: n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2
Output: false
Explanation: It is possible to reach and get stuck on both node 1 and node 2.

Example 2:

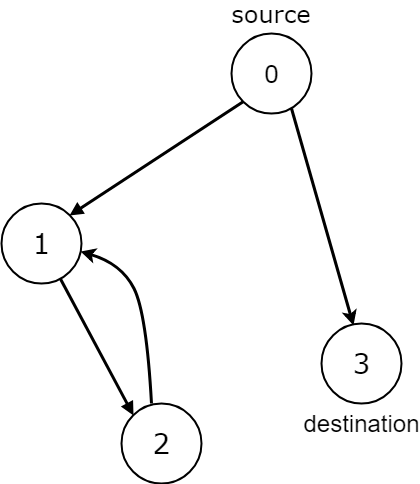
Input: n = 4, edges = [[0,1],[0,3],[1,2],[2,1]], source = 0, destination = 3
Output: false
Explanation: We have two possibilities: to end at node 3, or to loop over node 1 and node 2 indefinitely.

Example 3:

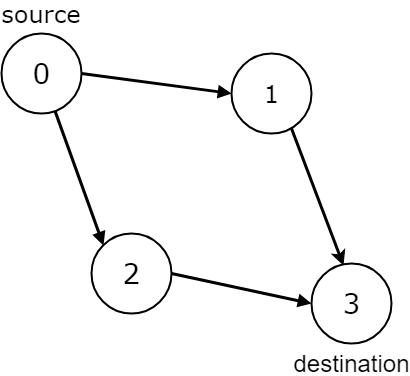
Input: n = 4, edges = [[0,1],[0,2],[1,3],[2,3]], source = 0, destination = 3
Output: true

Example 4:

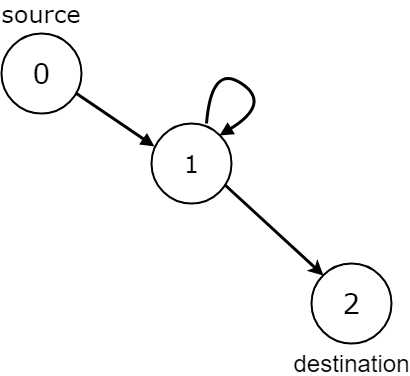
Input: n = 3, edges = [[0,1],[1,1],[1,2]], source = 0, destination = 2
Output: false
Explanation: All paths from the source node end at the destination node, but there are an infinite number of paths, 
such as 0-1-2, 0-1-1-2, 0-1-1-1-2, 0-1-1-1-1-2, and so on.

Example 5:

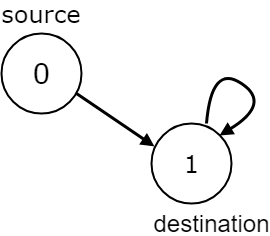
Input: n = 2, edges = [[0,1],[1,1]], source = 0, destination = 1
Output: false
Explanation: There is infinite self-loop at destination node.

Note:

1. The given graph may have self loops and parallel edges.
2. The number of nodes n in the graph is between 1 and 10000
3. The number of edges in the graph is between 0 and 10000
4. 0 <= edges.length <= 10000
5. edges[i].length == 2
6. 0 <= source <= n - 1
7. 0 <= destination <= n - 1

从始点到终点的所有路径。

给定有向图的边 edges，以及该图的始点 source 和目标终点 destination，确定从始点 source 出发的所有路径是否最终结束于目标终点 destination，即：

• 从始点 source 到目标终点 destination 存在至少一条路径
• 如果存在从始点 source 到没有出边的节点的路径，则该节点就是路径终点。
• 从始点source到目标终点 destination 可能路径数是有限数字
• 当从始点 source 出发的所有路径都可以到达目标终点 destination 时返回 true，否则返回 false。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/all-paths-from-source-lead-to-destination
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这是一道有向图的题。题目的意思解释的很清楚，给了起点，终点，所有的边，请你判断是不是所有从起点开始的边都能带你去到终点。

遇到图的题，绝大部分还是先创建图，再用DFS或者BFS去遍历。这个题需要注意的点是

• 当遇到一个终点（这个点没有next节点），判断这个点是不是 destination
  • hashmap的做法是判断这个点在 hashmap 里是否能找到，如果找不到，就判断他不是destination；或者说这条路径不在起点 - 终点的路径上
• 判断图中是否有环 - 用hashset判断是否访问过或者用染色法
  • 当遍历当前点的邻居们的时候，如果发现任何一个邻居已经在 hashset 存在了，则发现了环，return false。
  • 判断环是因为如果有环的话那说明一定有某条路径不在起点 - 终点的路径上

思路不难想，代码的实现需要多练，面试才会写的6。

时间O(V + E)

空间O(V + E)

Java实现 - hashmap建图

class Solution {
    public boolean leadsToDestination(int n, int[][] edges, int source, int destination) {
        // build the graph
        HashMap<Integer, List<Integer>> graph = new HashMap<>();
        for (int[] edge : edges) {
            graph.putIfAbsent(edge[0], new ArrayList<>());
            graph.get(edge[0]).add(edge[1]);
        }
        return helper(graph, new HashSet<>(), source, destination);
    }

    private boolean helper(Map<Integer, List<Integer>> graph, Set<Integer> visited, int cur, int end) {
        // base case
        if (!graph.containsKey(cur)) {
            return cur == end;
        }
        visited.add(cur);
        for (int neighbor : graph.get(cur)) {
            if (visited.contains(neighbor) || !helper(graph, visited, neighbor, end)) {
                return false;
            }
        }
        visited.remove(cur);
        return true;
    }
}

 

Java实现 - list建图

class Solution {
    public boolean leadsToDestination(int n, int[][] edges, int source, int destination) {
        List<Integer>[] graph = new List[n];
        int[] colors = new int[n];
        buildGraph(graph, edges);
        return helper(graph, source, destination, colors);
    }

    private void buildGraph(List<Integer>[] graph, int[][] edges) {
        for (int[] edge : edges) {
            int from = edge[0];
            int to = edge[1];
            if (graph[from] == null) {
                graph[from] = new LinkedList<>();
            }
            graph[from].add(to);
        }
    }

    private boolean helper(List<Integer>[] graph, int source, int destination, int[] colors) {
        // base case
        if (graph[source] == null || graph[source].size() == 0) {
            return source == destination;
        }
        colors[source] = 1;
        for (int next : graph[source]) {
            // if visited
            if (colors[next] == 1) {
                return false;
            }
            if (colors[next] == 0 && !helper(graph, next, destination, colors)) {
                return false;
            }
            colors[source] = 0;
        }
        return true;
    }
}

 

LeetCode 题目总结