[LeetCode] 785. Is Graph Bipartite?

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

• There are no self-edges (graph[u] does not contain u).
• There are no parallel edges (graph[u] does not contain duplicate values).
• If v is in graph[u], then u is in graph[v] (the graph is undirected).
• The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

Example 1:

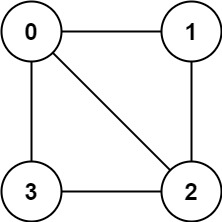
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

Constraints:

• graph.length == n
• 1 <= n <= 100
• 0 <= graph[u].length < n
• 0 <= graph[u][i] <= n - 1
• graph[u] does not contain u.
• All the values of graph[u] are unique.
• If graph[u] contains v, then graph[v] contains u.

判断二分图。

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：
不存在自环（graph[u] 不包含 u）。
不存在平行边（graph[u] 不包含重复值）。
如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。
二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/is-graph-bipartite
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

我这里提供两种做法，其实都是涂色法，只是涂色的方式不同。首先是BFS。可以参考这个油管视频，深刻理解涂色法。大致的思路是，当你遍历graph里面的节点的时候，当遇到某一个节点，如果他没有被染色，你就试图给他染成某一种颜色，但是对于这个点的所有邻居节点，需要给他们染成一个别的颜色以区分开。照着这个思路，你需要确保邻居节点被染成不同的颜色。如果遍历结束，所有节点都被染色成功，则说明是一个二分图；如果在染色过程中发现有节点已经被染色但是染色错误，则这个图不是二分图。既然是BFS，就会需要一个queue来遍历图的每一个节点。其他部分请参见代码。我这里给的染色是1和2，代表两种不同的颜色，如果遇到某个节点与其邻居节点颜色一样则返回false。

时间O(V + E)

空间O(n)

Java实现

class Solution {
    public boolean isBipartite(int[][] graph) {
        // BFS
        // 0(not meet), 1(black), 2(white)
        int[] visited = new int[graph.length];
        for (int i = 0; i < graph.length; i++) {
            if (graph[i].length != 0 && visited[i] == 0) {
                visited[i] = 1;
                Queue<Integer> queue = new LinkedList<>();
                queue.offer(i);
                while (!queue.isEmpty()) {
                    int cur = queue.poll();
                    for (int c : graph[cur]) {
                        if (visited[c] == 0) {
                            visited[c] = (visited[cur] == 1) ? 2 : 1;
                            queue.offer(c);
                        } else {
                            if (visited[c] == visited[cur]) {
                                return false;
                            }
                        }
                    }
                }
            }
        }
        return true;
    }
}

 

JavaScript实现

/**
 * @param {number[][]} graph
 * @return {boolean}
 */
var isBipartite = function (graph) {
    let visited = new Array(graph.length).fill(0);
    for (let i = 0; i < graph.length; i++) {
        if (graph[i].length && visited[i] == 0) {
            visited[i] = 1;
            let queue = [];
            queue.push(i);
            while (queue.length) {
                let cur = queue.shift();
                for (let next of graph[cur]) {
                    if (visited[next] == 0) {
                        visited[next] = visited[cur] == 1 ? 2 : 1;
                        queue.push(next);
                    } else {
                        if (visited[cur] === visited[next]) {
                            return false;
                        }
                    }
                }
            }
        }
    }
    return true;
};

 

DFS思路跟BFS几乎没什么两样，无非是DFS往下层寻找的时候，涂色是按一正一负这样涂的，而BFS是涂成1或2。

时间O(V + E)

空间O(n)

Java实现

class Solution {
    public boolean isBipartite(int[][] graph) {
        int[] visited = new int[graph.length];
        for (int i = 0; i < graph.length; i++) {
            // 当前点没有被访问过且染色失败，返回false
            if (visited[i] == 0 && !dfs(graph, visited, 1, i)) {
                return false;
            }
        }
        return true;
    }

    /**
     * @param graph   图
     * @param node    当前处理的顶点
     * @param color   当前顶点即将被染的颜色
     * @param visited 记录顶点是否被访问过
     * @return 成功染色，返回true，失败染色返回false
     */
    private boolean dfs(int[][] graph, int[] visited, int color, int node) {
        if (visited[node] != 0) {
            return visited[node] == color;
        } else {
            visited[node] = color;
            for (int nei : graph[node]) {
                if (!dfs(graph, visited, -color, nei)) {
                    return false;
                }
            }
        }
        return true;
    }
}

 

相关题目

785. Is Graph Bipartite

886. Possible Bipartition

LeetCode 题目总结