[LeetCode] 918. Maximum Sum Circular Subarray

Given a circular integer array nums of length n, return the maximum possible sum of a non-empty subarray of nums.

A circular array means the end of the array connects to the beginning of the array. Formally, the next element of nums[i] is nums[(i + 1) % n] and the previous element of nums[i] is nums[(i - 1 + n) % n].

A subarray may only include each element of the fixed buffer nums at most once. Formally, for a subarray nums[i], nums[i + 1], ..., nums[j], there does not exist i <= k1, k2 <= j with k1 % n == k2 % n.

Example 1:

Input: [1,-2,3,-2]
Output: 3
Explanation: Subarray [3] has maximum sum 3

Example 2:

Input: [5,-3,5]
Output: 10
Explanation: Subarray [5,5] has maximum sum 5 + 5 = 10

Example 3:

Input: [3,-1,2,-1]
Output: 4
Explanation: Subarray [2,-1,3] has maximum sum 2 + (-1) + 3 = 4

Example 4:

Input: [3,-2,2,-3]
Output: 3
Explanation: Subarray [3] and [3,-2,2] both have maximum sum 3

Example 5:

Input: [-2,-3,-1]
Output: -1
Explanation: Subarray [-1] has maximum sum -1

Constraints:

• n == nums.length
• 1 <= n <= 3 * 104
• -3 * 104 <= nums[i] <= 3 * 104

环形子数组的最大和。

给定一个长度为 n 的环形整数数组 nums ，返回 nums 的非空 子数组 的最大可能和 。

环形数组 意味着数组的末端将会与开头相连呈环状。形式上， nums[i] 的下一个元素是 nums[(i + 1) % n] ， nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。

子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上，对于子数组 nums[i], nums[i + 1], ..., nums[j] ，不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/maximum-sum-circular-subarray
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

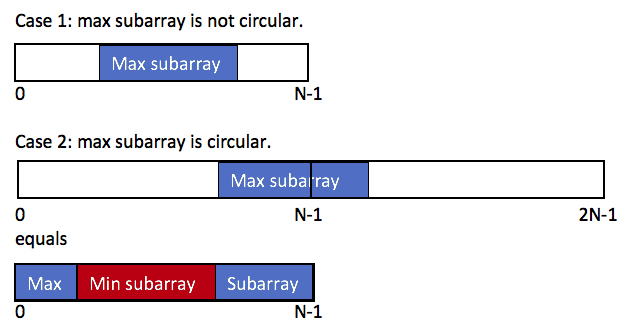
这个题一开始读题的时候让我觉得是53题的 followup，但是这个题用53题DP的思想好像还不太能套用得上去，因为有可能最大的子数组是断开的。这个题我参考了lee大神的帖子。基本思路是因为 input 数组可能是环形的，所以有可能最后最大的子数组有可能是如下几种情形，如下图所示

• 一种是直接在原数组的中间
• 一种是在原数组前半段截取一点出来，在后半段也截取一点出来

对于第一种情况，其实就跟53题是一样的；但是对于第二种情况，如果我们需要得知断开的，最大的子数组，我们可以反过来去求连续的，最小的子数组的和，然后用整个数组的和减去连续的，最小的子数组的和。唯一的 corner case 是如果整个数组都是由负数组成的，那么整个数组的和 sum 跟数组连续的，最小的子数组的和是一样的。最后比较的时候，需要看看到底是 case 1 的结果更大，还是 case 2 里面的 min subarray 更小。

注意代码里全局最大值和全局最小值为什么设置成第一个元素的值而不能设置成 0 是因为如果整个数组都是负数的话，环形数组的最大和也不可能是 0 。

时间O(n)

空间O(1)

Java实现

class Solution {
    public int maxSubarraySumCircular(int[] nums) {
        int total = 0;
        // 全局的最大值
        int maxSum = nums[0];
        // 当前的最大值
        int curMax = 0;
        // 全局的最小值
        int minSum = nums[0];
        // 当前的最小值
        int curMin = 0;
        for (int num : nums) {
            curMax = Math.max(curMax + num, num);
            maxSum = Math.max(maxSum, curMax);
            curMin = Math.min(curMin + num, num);
            minSum = Math.min(minSum, curMin);
            total += num;
        }
        return maxSum > 0 ? Math.max(maxSum, total - minSum) : maxSum;
    }
}

 

我再提供一个使用额外空间的做法，跟53题的代码很像。注意求最小子数组的时候扫描的范围，因为如果求最小子数组，那么说明最大子数组一定是断开的，所以求最小子数组的时候要避开第一个和最后一个位置。

时间O(n)

空间O(n)

Java实现

class Solution {
    public int maxSubarraySumCircular(int[] nums) {
        int[] dp = new int[nums.length]; // dp[i]用来记录以nums[i]结尾的最大子序列和
        dp[0] = nums[0]; // 初始化dp
        int max = dp[0]; // 最大子序列和
        int sum = dp[0]; // 整个数组的和

        // 求最大子序列和，见53题
        for (int i = 1; i < dp.length; i++) {
            sum += nums[i];
            dp[i] = nums[i] + Math.max(dp[i - 1], 0);
            max = Math.max(dp[i], max);
        }

        int min = 0; // 开始求A[1]~A[n-1]上的最小子序列和
        for (int i = 1; i < dp.length - 1; i++) {
            dp[i] = nums[i] + Math.min(0, dp[i - 1]);
            min = Math.min(dp[i], min);
        }
        return Math.max(sum - min, max);
    }
}

 

相关题目

53. Maximum Subarray

152. Maximum Product Subarray

918. Maximum Sum Circular Subarray

978. Longest Turbulent Subarray

LeetCode 题目总结