[LeetCode] 62. Unique Paths

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

Example 1:

Input: m = 3, n = 7
Output: 28

Example 2:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down

Example 3:

Input: m = 7, n = 3
Output: 28

Example 4:

Input: m = 3, n = 3
Output: 6

Constraints:

• 1 <= m, n <= 100
• It's guaranteed that the answer will be less than or equal to 2 * 109.

不同路径。

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/unique-paths
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题意是一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start”）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。问总共有多少条不同的路径。

这一题也是 DP 的基础题，一定要掌握。这里我提供三种做法，

• 自上而下（自上而下又叫递归 + memo）
• 自下而上
• 节省空间的自下而上

DP自上而下

时间O(mn)

空间O(mn)

Java实现

class Solution {
    int[][] memo;
    
    public int uniquePaths(int m, int n) {
        memo = new int[m][n];
        return dp(m - 1, n - 1);
    }
    
    private int dp(int i, int j) {
        if (i == 0 && j == 0) {
            return 1;
        }
        if (i < 0 || j < 0) {
            return 0;
        }
        if (memo[i][j] > 0) {
            return memo[i][j];
        }
        memo[i][j] = dp(i - 1, j) + dp(i, j - 1);
        return memo[i][j];
    }
}

// dp自上而下

 

DP自下而上，先确定矩阵边缘上的点的DP值，然后再考虑中间的点

时间O(mn)

空间O(mn)

Java实现

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        dp[0][0] = 1;
        for (int i = 1; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int j = 1; j < n; j++) {
            dp[0][j] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] += dp[i - 1][j];
                dp[i][j] += dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
}
// dp自下而上

 

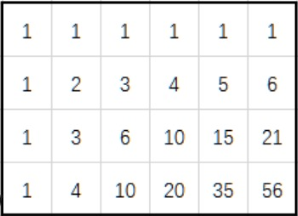
节省空间的一维 DP。一维 DP 的思路是逐行扫描。首先初始化一个长度为 n 的数组，并初始化第一个坐标为 1（也就是坐标上0, 0的位置）。接着往右边扫描，每一个坐标的值是当前位置的 DP 值 + 他左边一个位置的 DP 值。根据下图跑一下代码，第7行，第一遍跑的时候，一开始 res[j] = res[1] = 0 + res[0] = 0 + 1 = 1；接着 res[2] = 0 + 1 = 1。以此类推得到第一行的dp值是 [1, 1, 1, 1, 1, 1]。再遍历第二行，得到 [1, 2, 3, 4, 5, 6]；第三行 [1, 3, 6, 10, 15, 21] 和第四行 [1, 4, 10, 20, 35, 56]。这个思路非常巧妙，需要多多体会。

时间O(mn)

空间O(n)

 

Java实现

class Solution {
    public int uniquePaths(int m, int n) {
        int[] res = new int[n];
        Arrays.fill(res, 1);
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                res[j] += res[j - 1];
            }
        }
        return res[n - 1];
    }
}
// 节省空间的自下而上

 

JavaScript实现

/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var uniquePaths = function (m, n) {
    let res = new Array(n).fill(0);
    res[0] = 1;
    for (let i = 0; i < m; i++) {
        for (let j = 1; j < n; j++) {
            res[j] = res[j] + res[j - 1];
        }
        // console.log(res);
    }
    return res[n - 1];
};

 

相关题目

62. Unique Paths

63. Unique Paths II

64. Minimum Path Sum

LeetCode 题目总结