[LeetCode] 509. Fibonacci Number
The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,
F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), for N > 1.
Given N, calculate F(N).
Example 1:
Input: 2 Output: 1 Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.
Example 2:
Input: 3 Output: 2 Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.
Example 3:
Input: 4 Output: 3 Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.
Note:
0 ≤ N ≤ 30.
斐波那契数列。
斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给你 n ，请计算 F(n) 。来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/fibonacci-number
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
题意很简单，求出斐波那契数列里面第 N 个数。这个题有好几个思路，分别是迭代，递归和动态规划。虽然是个基础题但是涉及到的思路还是比较全面的，故而都列出来。
迭代
时间O(n)
空间O(1)
1 /** 2 * @param {number} N 3 * @return {number} 4 */ 5 var fib = function(N) { 6 if (N <= 1) { 7 return N; 8 } 9 var a = 0; 10 var b = 1; 11 while (N > 1) { 12 var sum = a + b; 13 a = b; 14 b = sum; 15 N--; 16 } 17 return b; 18 };
递归
时间O(n)
空间O(n)
1 /** 2 * @param {number} N 3 * @return {number} 4 */ 5 var fib = function(N) { 6 if (N <= 1) { 7 return N; 8 } else { 9 return fib(N - 1) + fib(N - 2); 10 } 11 };
动态规划 - 自底向上
为什么这种做法叫自底向上呢？因为我们是从第一个斐波那契数一个个往后推导的。这样从更小的，已知的的问题的答案推导到更大的未知的答案的思想是自底向上。
时间O(n)
空间O(n)
JavaScript实现
1 /** 2 * @param {number} N 3 * @return {number} 4 */ 5 var fib = function(N) { 6 if (N <= 1) { 7 return N; 8 } 9 let dp = [N + 1]; 10 dp[0] = 0; 11 dp[1] = 1; 12 for (let i = 2; i <= N; i++) { 13 dp[i] = dp[i - 2] + dp[i - 1]; 14 } 15 return dp[N]; 16 };
Java实现
1 class Solution { 2 public int fib(int N) { 3 if (N <= 1) { 4 return N; 5 } 6 int[] dp = new int[N + 1]; 7 dp[0] = 0; 8 dp[1] = 1; 9 for (int i = 2; i <= N; i++) { 10 dp[i] = dp[i - 2] + dp[i - 1]; 11 } 12 return dp[N]; 13 } 14 }
动态规划 - 自上而下
为什么这种做法叫自上而下呢？是因为我们为了解决一个规模更大的问题，试图去看能否找到一个规模更小的问题的答案，从而推导出来更大的问题的答案的。这种做法的背后实际是一棵二叉树，参见这个截图。
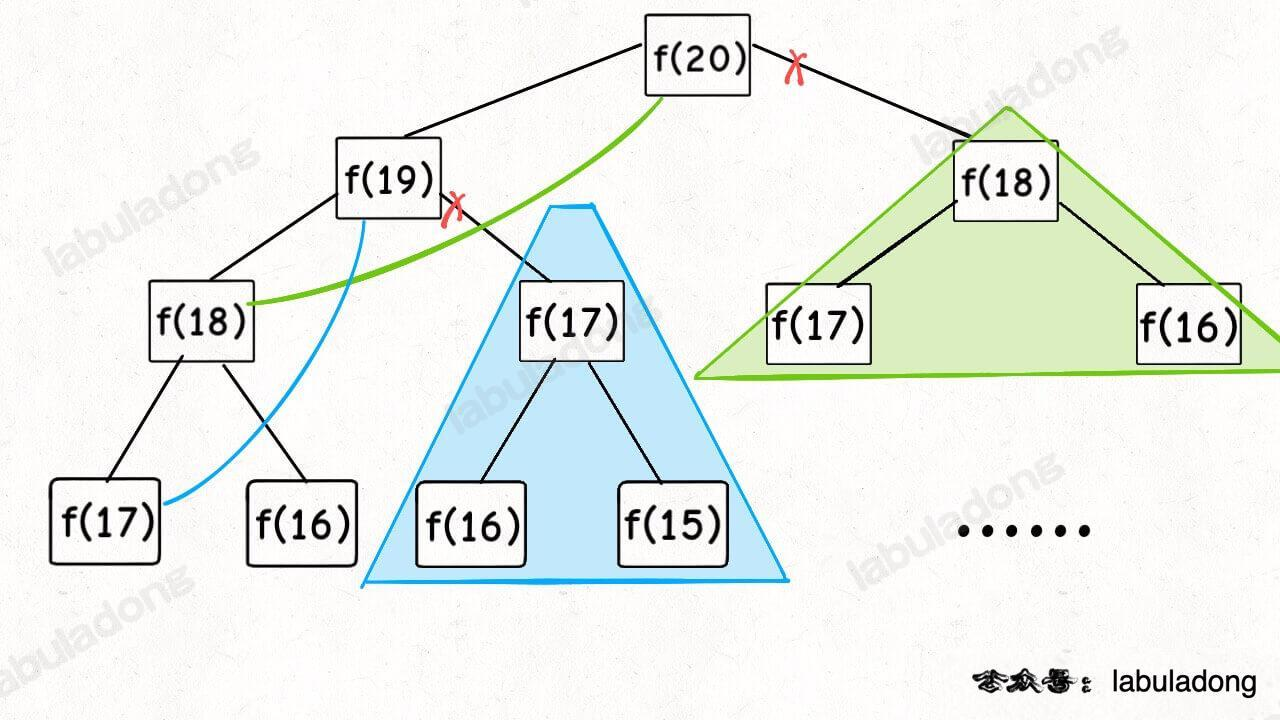
为了得到 f(20)，我们递归去找规模更小的子问题 f(19) 和 f(18)。
时间O(n)
空间O(n)
Java实现
1 class Solution { 2 public int fib(int n) { 3 int[] memo = new int[n + 1]; 4 return helper(memo, n); 5 } 6 7 private int helper(int[] memo, int n) { 8 if (n == 0 || n == 1) { 9 return n; 10 } 11 if (memo[n] != 0) { 12 return memo[n]; 13 } 14 memo[n] = helper(memo, n - 2) + helper(memo, n - 1); 15 return memo[n]; 16 } 17 }
相关题目
