[LeetCode] 240. Search a 2D Matrix II

Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

Example 1:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

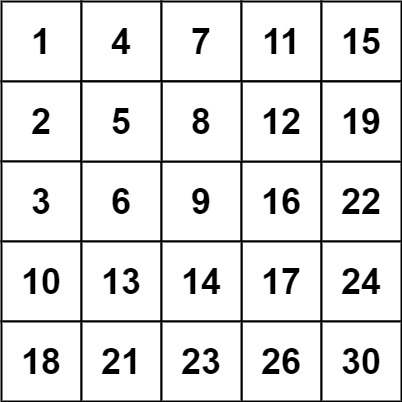
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -109 <= matix[i][j] <= 109
• All the integers in each row are sorted in ascending order.
• All the integers in each column are sorted in ascending order.
• -109 <= target <= 109

搜索二维矩阵II。

题意跟[LeetCode] 74. Search a 2D Matrix很接近，唯一的不同是matrix只是做到了每一行上的元素是有序的，每一列也是有序的，但是convert成一维数组后，一维数组并不能做到整体有序。

因为input的规律是每一行是有序的，每一列也是有序的，所以可以从数组的右上角（比如例子中的15好了）开始扫描，如果小于15，就往左；如果大于15，就一定在下一行。

时间O(m + n)

空间O(1)

JavaScript实现

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
    let row = 0;
    let col = matrix[0].length - 1;
    while (col >= 0 && row <= matrix.length - 1) {
        if (target === matrix[row][col]) {
            return true;
        } else if (target < matrix[row][col]) {
            col--;
        } else {
            row++;
        }
    }
    return false;
};

 

Java实现

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        int row = 0;
        int col = matrix[0].length - 1;
        while (row < m && col >= 0) {
            if (matrix[row][col] == target) {
                return true;
            } else if (matrix[row][col] < target) {
                row++;
            } else if (matrix[row][col] > target) {
                col--;
            }
        }
        return false;
    }
}

 

相关题目

74. Search a 2D Matrix

240. Search a 2D Matrix II

LeetCode 题目总结