ST表学习笔记
st表是一种的数据结构。运用倍增思想,可以维护 RMQ (区间最值问题),预处理 \(O(N\log N)\) ,查询 \(O(1)\) 。
以求区间最大值为例。
预处理
用一个二维数组 \(f[j][i]\) 来存储一定区间内的最大值,其中 \(j\) 表示区间长度为 \(2^{j}\) , \(i\) 表示区间起点。即 \(f[j][i]\) 表示 \(\max\limits_{i\le k \le i+2^j}A_k\) 。
将一个区间分为两小段,用两小段预处理出区间的最值(似乎是 dp 思想)。
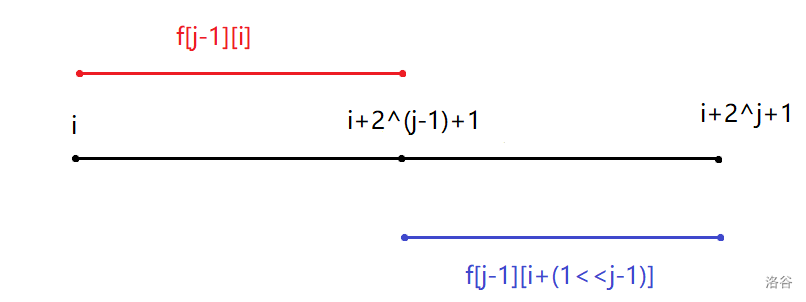
code:
int f[25][Max];//长度2^25足够了
inline void build(){
for(int i = 1;i <= n;i++){
st[0][i]=a[i];
}
for(int j = 1;j <= 25;j++){
for(int i = 1;i+(1<<j)-1 <= n;i++){
st[j][i]=max(st[j-1][i],st[j-1][i+(1<<(j-1))]);
}
}
}
查询
令 \(k = log_2(r-l+1)\) ,比较 \([l,l+2^k-1]\) 和 \([r-2^k+1,r]\) 的最大值。
因为 \(2^k\) 为区间长度所以是 \(l+2^k-1\) , \(r-2^k+1\)。
证明 \([l,l+2^k-1]\) 和 \([r-2^k+1,r]\) 一定能覆盖 \([l,r]\) :
当 \(l+2^k-1=r\) 时,有\(k=log_2(r-l+1)\)
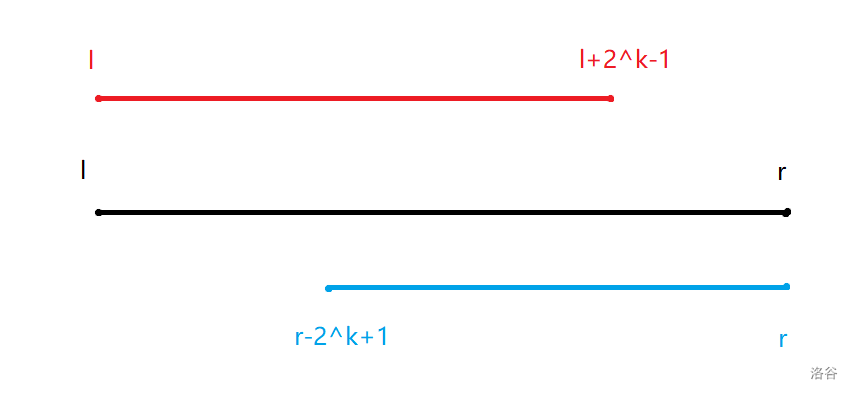
code:
inline int askMax(int l,int r){
int k=__lg(r-l+1);
return max(st[k][l],st[k][r-(1<<k)+1]);
}
补充(?)
__lg() 函数可以在 \(O(1)\) 时间内算出一个数的 \(log_2\)
关于为什么要声明成 \(f[长度][起点]\) : intR 说快。


