tarjan学习笔记

tarjan学习笔记

为方便说明，$x$ 指当前节点， $y$ 指当前节点的子节点， $fa$ 指当前节点的父亲节点。

0.前置知识

• 搜索树

  在一张连通图中，所有的节点以及发生递归的边共同构成一棵搜索树。如果这张图不连通，则构成搜索森林。

  

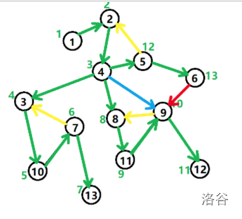
  如图 从The_Shadow_Dragon博客上扣下来的

  • 搜索树上的边，称为 树边（绿色）。
  • 从祖先指向后代的非树边，称为 前向边（蓝色）。
  • 从后代指向祖先的非树边，称为 返祖边（黄色）。
  • 从子树中的节点指向另一子树节点的边，称为 横叉边（红色）。

  ---

  有向图的树边是单向的，无向图的树边是双向的（无向图中由儿子到父亲的边似乎不是树边？）。

• dfn（时间戳）

  在对图的遍历中，各个顶点被遍历的顺序（ $dfn[i]$ 表示节点 $i$ 第几次被遍历到）

• low（追溯值）

  • 定义

    蓝书中给出的概念是：

    设 $subtree(x)$ 表示搜索树中以 $x$ 为根的子树。$low[x]$定义为以下节点的时间戳的最小值。

    1. $subtree(x)$ 中的节点
    2. 通过1条不在搜索树上的边，能够到达 $subtree(x)$ 的节点

    ---

    可以理解为，一个节点通过树边或一个非树边可以到达（回溯）的最先被遍历到的节点。（ $low[i]$ 表示在节点 $i$ 可以到达的最小的 $dfn$ 值）

    可以看出当当前节点有返祖边时，low将被更新为更小的值

  • $low$ 的更新方式

    设 当前访问的节点为 $x$, $x$ 能到达的点为 $y$

    • 初始化 dfn[x]=low[x]=++tot

    • 若 $y$ 未被遍历到，则该边为树边，递归访问 $y$ , 因为 $low$ 的性质，令 $low_x=min(low_x,low_y)$

    • 若 $y$ 被遍历过，则该边为返祖边或横叉边（存疑），因为 $low$ 的性质,可以回到 $x$，令 $low_x=min(low_x,dfn_y)$

1. tarjan与有向图强连通分量

• 相关定义

  • 强连通图

    在一个有向图中，若从任意一点可以到达其他所有点，则称之为强连通图

  • 强连通分量（SCC）

    一个有向图中的极大强连通子图（强连通图的强连通分量是它本身）

    $\small {极大强连通子图指一个不能加入另外的点的强连通子图（一个强连通子图可能包含一个或多个小的强连通子图）}$

• 强连通分量判定法则

  其实是求一个节点属于哪个强连通分量

  • 判断方式

    $dfn_x=low_x$ 可以理解为 节点 $x$ 能返回到最早的节点就是 $x$ 本身,则节点 $x$ 到 $s.top()$ 内的所有节点为一个强连通分量。

  • 常用变量

    cnt：强连通图数量

    dfn[]：节点 $i$ 第几次被遍历到

    low[]：在节点 $i$ 存在的路径中，最小的 $dfn$ 值

    belong[]：节点 $i$ 属于第几个强连通图

    inStack[]：节点 $i$ 是否在栈中

    tot：当前已有几个节点被访问

  • 代码实现

    inline void tarjan(int x){
      dfn[x]=low[x]=++tot;
      s.push(x);
      inStack[x]=1;
      for(int i = Head[x];i;i=Next[i]){
        int y=Ver[i];
        if(!dfn[y]){
          dfs(y);
          low[x]=min(low[x],low[y]);
        }
        else 
          if(inStack[y])low[x]=min(low[x],dfn[y]);
      }
      if(dfn[x]==low[x]){
        cnt++;
        while(s.top()!=x){
          belong[s.top()]=cnt;
          inStack[s.top()]=0;
          s.pop();
        }
        inStack[x]=0;
        belong[x]=cnt;
        s.pop();
    
      }
    }
    

• 缩点

  因为一个节点只属于一个强连通分量，所以对于一些问题，我们可以将一个强连通分量看做一个点。

  即若存在有向边 x->y，若 $belong_x \ne belong_y$ 则建立一条边 belong[x] -> belong[y]。

  • 代码实现

    for(int i = 1;i <= n;i++){
    	for(int j=A.Head[i];j;j=A.Next[j]){
    		int y=A.Ver[j];
    		if(belong[i]!=belong[y]){
    			A_.add(belong[i],belong[y]);
    			outp[belong[i]]++;
    		}
    	}
    }
    

  $\small{ps：A,A\_ 为封装的链式前向星。}$

• 拓展

  缩点后，图成为一个DAG（有向无环图）。对于某些题我们可以使用 DAGdp 或 SPFA 在DAG上求最长路。

  • DAGdp

    顾名思义是在有向无环图上的dp，用拓扑序作为求出dp顺序，需要在缩点事记录每个点的入度。（拓扑序需要根据点的入度求出）

    $\small{感觉就是个BFS}$

    • 代码实现

      inline void dagdp(){
      	for(int i = 1;i <= cnt;i++){
      		if(!inp[i]){
      			q.push(i);
      			f[i]=d[i];
      		}
      	}
      	while(!q.empty()){
      		int t=q.front();
      		q.pop();
      		for(int i = A_.Head[t];i;i=A_.Next[i]){
      			int y=A_.Ver[i];
      			inp[y]--;
      			f[y]=max(f[y],f[t]+d[y]);
      			if(!inp[y]) q.push(y);
      		}
      	}
      }
      

  • SPFA

    不想写了。

    dij 因为贪心的思想，所以跑不了最长路。

2. tarjan与无向图

• 相关定义

  • 割点

    在无向图中，删去后使得连通分量数增加的结点称为割点。

  • 割边

    在无向图中，删去后使得连通分量数增加的边称为割边（桥）

  • 点双连通图

    不存在割点的无向连通图称为点双连通图。

  • 点双连通分量（V-BCC）

    一张图的极大点双连通子图称为点双连通分量。

  • 边双连通图

    不存在割边的无向连通图称为边双连通图。

  • 边双连通分量（E-BCC）

    一张图的极大边双连通子图称为边双连通分量。

• tarjan求割边（割边判定法则）

  • 判断方式

    $low_y > dfn_x$ 可以理解为从 $subtree(y)$ 出发，不经过 $(x,y)$ ，不管走那条边，都不能到达 $x$ 或比 $x$ 更早访问的节点，最远只能到达 $y$（必经之边），故 $(x,y)$ 一定是割边。

  • 有关父节点与重边

    因为无向边的缘故，节点 $x$ 必定可以访问到它的父节点 $fa$ 。因为 $(x,fa)$ 为树边，跟据 $low$ 的定义，不可以用 $fa$ 来更新 $x$ 。

    但若有重边（ $fa$ 与 $x$ 有多个边相连），则只有一条 $(x,fa)$ 算作树边。所以有重边时，能用 $fa$ 来更新 $x$。

  • 代码实现

    void tarjan(int x,int fa){
        dfn[x]=low[x]=++tot;
        bool fae=0;//是否已经有父亲跟当前节点相连
        for(int i = A.Head[x];i;i=A.Next[i]){
            int y=A.Ver[i];
            if(!dfn[y]){
                tarjan(y,x);
                low[x]=min(low[x],low[y]);
                if(low[y]>dfn[x]){
                      bridge[i]=bridge[i^1]=1;
                }
            }
            else{ 
                if(y==fa && !fae) fae=1;
                else low[x]=min(low[x],dfn[y]);
            } 
        }
    }
    

• tarjan求割点（割点判定法则）

  • 判定为割点有两种情况：

    1.此节点满足 $low_y \ge dfn_x$ 且为的搜索树的根节点并有两个及以上子树。

    2.此节点满足 $low_y \ge dfn_x$ 且不是搜索树的根节点。

    ---

    $low[y] \ge dfn[x]$ 可以理解为从 $subtree(y)$ 出发，最远只能到达 $x$ 而不能到达比 $x$ 更早访问的节点（必经之点），故 $x$ 一定是割点。

  • 有关父节点与重边（与割边相比较）

    蓝书上说：“因为割点判定法则是小于等于号,所以在求割点时，不必考虑父节点和重边问题”。

    我觉得比较抽象（反正我看不懂），所以我们不妨形象地解释一下：当此节点为割点时，无论有几条边与节点相连，删除此节点后都会断掉，所以有多少种边与此点相连都无所谓。

    

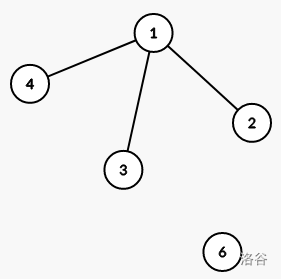
  • 代码实现

    void tarjan(int x,int root){
        dfn[x]=low[x]=++tot;
        int ch=0;
        for(int i = A.Head[x];i;i=A.Next[i]){
            int y=A.Ver[i];
            if(!dfn[y]){
                tarjan(y,root);
                low[x]=min(low[x],low[y]);
                if(low[y]>=dfn[x]){
    				ch++;
                    if(x!=root||ch>=2){
                        cut[x]=1;
                    } 
                }  
            }
            else low[x]=min(low[x],dfn[y]);
        }
    }
    

    if(x!=root||ch>=2) 只是判断根节点是否有两个根节点，非根节点可以全部通过。

• 求边双连通分量（e-DCC）

  • 先用tarjan求出所有的割边 然后用dfs求出每一个点属于哪个边双连通分量。
  • 代码实现

    void dfs(int x){
        belong[x]=cnt;
        for(int i = A.Head[x];i;i=A.Next[i]){
            int y=A.Ver[i];
            if(!bridge[i]&&!belong[y]) dfs(y);
        }
    }
    

• 求点双连通分量（v-DCC）

  一个可能属于多个 v-DCC

  • 流程：

    2. 当一个节点第一次被访问时，把该节点入栈。

    3. 当 $low_y \ge dfn_x$成立时，此时 $x$ 是割点，$subtree(y)$ 为一个点双连通分量。无论 $x$ 是否为根，都要：

       （1）从栈中不断弹出节点，直至节点 $y$ 被弹出。

       （2）刚才弹出的所有节点与割点 $x$ 一起构成一个 v-DCC。

    解释：

    • 不弹栈直到 $x$ 的原因：可能将其他子树的节点弹出。
    • 用do while 的原因：可能 $subtree(y)$ 就一个节点（ $y$ 本身）

  • 代码实现

    void tarjan(int x,int root){
        dfn[x]=low[x]=++tot;
        int ch=0;
        s.push(x);
        if(x==root&&A.Head[x]==0){//孤立节点
            ans[++cnt].push_back(x);
            return;
        }
        for(int i=A.Head[x];i;i=A.Next[i]){
            int y=A.Ver[i];
            if(!dfn[y]){
                tarjan(y,root);
                low[x]=min(low[x],low[y]);
                if(low[y]>=dfn[x]){
                    if(x!=root||ch>=2) cut[x]=1;
                    cnt++;
                    int t;
                    do{
                        t=s.top();
                        s.pop();
                        belong[t]=cnt;
                    }while(t!=y);
                    belong[x]=cnt;
                }
            }
            else low[x]=min(low[x],dfn[y]);
        }
    }