L2-006. 树的遍历

L2-006. 树的遍历

给定一棵二叉树的后序遍历和中序遍历，请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。

输入格式：

输入第一行给出一个正整数N（<=30），是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。

输出格式：

在一行中输出该树的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

输入样例：

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

输出样例：

4 1 6 3 5 7 2

思路：我没有学过数据结构，也就是了解过堆和线段树，利用二叉树的遍历来还原二叉树也是蛮有意思的。

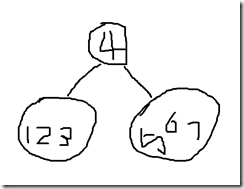
首先观察后序遍历，根据后序遍历的特点，可以发现最后一个节点一定是子树根节点，所以样例中的4便是祖先节点。然后再观察中序遍历，中序遍历的特点就是先把左子树的节点输出，在输出根节点，在输出右子树。根据前序遍历，就可以发现，根节点的左子树集合和右子树集合。

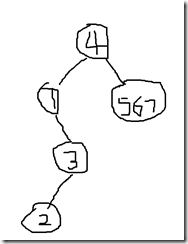
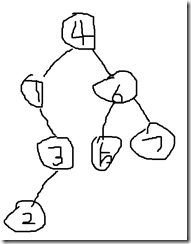
不管二叉树是如何遍历的，每子颗树上节点一定是在一个挨在一起的，只是访问的先后顺序不同。然后观察4的左子树，利用后序遍历可以找的左子树的根节点为1，在中序遍历中观察1，发现他只有一个右子树{2，3}，利用后序遍历可知3是1的右子树，2是3的左子树。

同样的道理，对4的右子树的后序遍历进行见检查，发现6是右子树的根节点，利用中序遍历可知，6的左孩子为5，右孩子为7。

这样就把二叉树还原出来了。

#include "cstdio"
#include "algorithm"
#include "cstring"
using namespace std;
const int maxn = 10000+10;
int res[maxn], pos[maxn], in[maxn];
void build(int L, int R, int idx, int root) {
    if (L > R) return;
    res[idx] = pos[root];
    int i = L;
    while (in[i] != pos[root]) i++;
    build(L, i-1, idx*2+1, root-1-R+i);
    build(i+1, R, idx*2+2, root-1);
}
int main(int argc, char const *argv[])
{
    int N;
    scanf("%d", &N);
    for (int i = 0; i < 10000; i++) res[i] = -1;
    for (int i = 0; i < N; i++) scanf("%d", pos+i);
    for (int i = 0; i < N; i++) scanf("%d", in+i);
    build(0, N-1, 0, N-1);
    printf("%d", res[0]);
    int cnt = 1;
    int i = 1;
    while (cnt < N) {
        if (res[i] != -1) {
            printf(" %d", res[i]);
            cnt++;
        }
        i++;
    }
    printf("\n");
    return 0;
}