HDU Problem - 4810 Wall Painting【组合数学】
Wall Painting
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2706 Accepted Submission(s): 865
Problem Description
Ms.Fang loves painting very much. She paints GFW(Great Funny Wall) every day. Every day before painting, she produces a wonderful color of pigments by mixing water and some bags of pigments. On the K-th day, she will select K specific bags of pigments and mix
them to get a color of pigments which she will use that day. When she mixes a bag of pigments with color A and a bag of pigments with color B, she will get pigments with color A xor B.
When she mixes two bags of pigments with the same color, she will get color zero for some strange reasons. Now, her husband Mr.Fang has no idea about which K bags of pigments Ms.Fang will select on the K-th day. He wonders the sum of the colors Ms.Fang will get with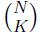 different plans.
different plans.
For example, assume n = 3, K = 2 and three bags of pigments with color 2, 1, 2. She can get color 3, 3, 0 with 3 different plans. In this instance, the answer Mr.Fang wants to get on the second day is 3 + 3 + 0 = 6.
Mr.Fang is so busy that he doesn’t want to spend too much time on it. Can you help him?
You should tell Mr.Fang the answer from the first day to the n-th day.
When she mixes two bags of pigments with the same color, she will get color zero for some strange reasons. Now, her husband Mr.Fang has no idea about which K bags of pigments Ms.Fang will select on the K-th day. He wonders the sum of the colors Ms.Fang will get with
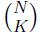 different plans.
different plans.For example, assume n = 3, K = 2 and three bags of pigments with color 2, 1, 2. She can get color 3, 3, 0 with 3 different plans. In this instance, the answer Mr.Fang wants to get on the second day is 3 + 3 + 0 = 6.
Mr.Fang is so busy that he doesn’t want to spend too much time on it. Can you help him?
You should tell Mr.Fang the answer from the first day to the n-th day.
Input
There are several test cases, please process till EOF.
For each test case, the first line contains a single integer N(1 <= N <= 103).The second line contains N integers. The i-th integer represents the color of the pigments in the i-th bag.
For each test case, the first line contains a single integer N(1 <= N <= 103).The second line contains N integers. The i-th integer represents the color of the pigments in the i-th bag.
Output
For each test case, output N integers in a line representing the answers(mod 106 +3) from the first day to the n-th day.
Sample Input
4
1 2 10 1
Sample Output
14 36 30 8
Source
Recommend
题意:
有n个数、n天。第i天从n个数中选出i个数进行按位与运算,求出每天这些数按位与的和。
思路:
任意多个数进行按位与,只要某一位有奇数个1,就可以一把这个数保存下来。因为是在所有的数中任意取,所以只要统计这些数的二进制位,求出每个值的贡献。然后用组合。快速幂+费马小定理会超时,只能用杨辉三角。
copy
#include <map> #include <set> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <iostream> #include <stack> #include <cmath> #include <string> #include <vector> #include <cstdlib> //#include <bits/stdc++.h> //#define LOACL #define space " " using namespace std; typedef long long LL; //typedef __int64 Int; typedef pair<int, int> paii; const int INF = 0x3f3f3f3f; const double ESP = 1e-5; const double PI = acos(-1.0); const long long MOD = 1e6 + 3; const int MAXN = 1000 + 10; LL fac[MAXN]; LL C[MAXN][MAXN]; int bit[32]; void get_c() { for(int i = 0; i <= 1000; i++) C[i][0] = 1; for(int i = 1; i <= 1000; i++) { for(int j = 1; j <= i; j++) { C[i][j] = (C[i-1][j] + C[i-1][j-1]) % MOD; } } } LL myc(int x, int y) {return C[x][y];} int main() { int n, t; get_c(); while (scanf("%d", &n) != EOF) { memset(bit, 0, sizeof(bit)); for (int i = 0; i < n; i++) { scanf("%d", &t); for (int j = 0; j <= 30; j++) { if (t & (1<<j)) bit[j]++; } } for (int k = 1; k <= n; k++) { LL ans = 0; for (int i = 0; i <= 30; i++) { if (!bit[i]) continue; for (int j = 1; j <= k && j <= bit[i]; j += 2) { ans += myc(bit[i], j)*myc(n - bit[i], k - j)%MOD* (1<<i)%MOD; ans %= MOD; } } if (k != n) printf("%lld ", ans%MOD); else printf("%lld\n", ans%MOD); } } return 0; }
copy
本文作者: zprhhs
本文链接:https://www.cnblogs.com/cniwoq/p/6770780.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Java 中堆内存和栈内存上的数据分布和特点
· 开发中对象命名的一点思考
· .NET Core内存结构体系(Windows环境)底层原理浅谈
· C# 深度学习:对抗生成网络(GAN)训练头像生成模型
· .NET 适配 HarmonyOS 进展
· 手把手教你更优雅的享受 DeepSeek
· 腾讯元宝接入 DeepSeek R1 模型,支持深度思考 + 联网搜索,好用不卡机!
· AI工具推荐:领先的开源 AI 代码助手——Continue
· 探秘Transformer系列之(2)---总体架构
· V-Control:一个基于 .NET MAUI 的开箱即用的UI组件库