快速傅里叶变换(FFT)详解
感谢 路人黑的纸巾, 理论部分来源于地址
FFT原理:将多项式的系数表示转换为点值表示,从而进行卷积运算,理论上从\(O(n^2)\)降低到\(O(nlogn)\)。
\(f(x)\)为\(n\)次多项式,\(g(x)\)为\(m\)次多项式,\(f(x)\cdot g(x)\)为\(m+n\)次多项式。
将多项式从系数表示法转为点值表示法更加方便两个多项式相乘(只要将他们的对应项的做乘积即可),同时为了方便对递归算法进行改写,将点值扩展到它们的和向上最近的那个2的幂次方个:
这里\(r\)大于\(m+n\)最小的2的幂次方。然后选择\(r\)个插值点,使得每个点的函数计算的时间花费最小。
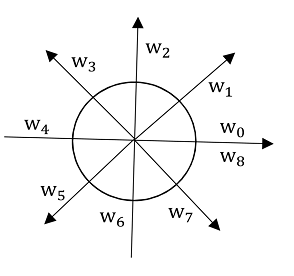
如上图当\(r=8\)时可以在一维复空间上这样等分的选择这8个插值点(每个点是单位圆上的等分点),是因为这些点有以下的几个性质可以用来减少计算量
性质
-
每个插值点:\(w_r^k=cos\frac{k}{r}2\pi + isin\frac{k}{r}2\pi,(k=0,...,r-1)\)
-
\(w_{2r}^{2k}=w_r^k\)
证:\(w_{2r}^{2k}=cos\frac{2k}{2r}2\pi+isin\frac{2k}{2r}2\pi=cos\frac{k}{r}2\pi+isin\frac{k}{r}2\pi=w_r^k\)
-
\(w_r^{k+\frac{r}{2}}=-w_r^{k}\)
证:\(w_r^{k+\frac{r}{2}}=cos\frac{k+\frac{r}{2}}{r}2\pi+isin(\frac{k+\frac{r}{2}}{r}2\pi)=cos(\frac{k}{r}2\pi+\pi)+isin(\frac{k}{r}2\pi+\pi)=-w_r^k\)
-
\(w_n^0=w_n^n\)
-
\(w_n^iw_n^j=w_n^{i+j}\)(复数乘法运算规律)
过程
首先对多项式进行整理有:
这里有\(t_1(x) = \sum_{i=0}^{i=\frac{r}{2}-1}a_{2i}x^i\), \(t_2(x) = \sum_{i=0}^{i=\frac{r}{2}-1}a_{2i+1}x^i\)。
设\((k<\frac{r}{2})\),\(w^k_r\)带入有:
将\(w_r^{k+\frac{n}{2}}\)带入有:
可以发现两个问题:
- 计算\(w_r^k\)时只需要在计算前一半的时候将符号进行改变,就能得到关于原点对称的另外一个值,就不需要单独的在计算一次计算。
- 计算\(w_r^k\)的过程实际上是将该问题分解成为两个不相交的子问题,每个子问题可以继续向下递归求解。
以\(w_8^0\)的计算过程为例:
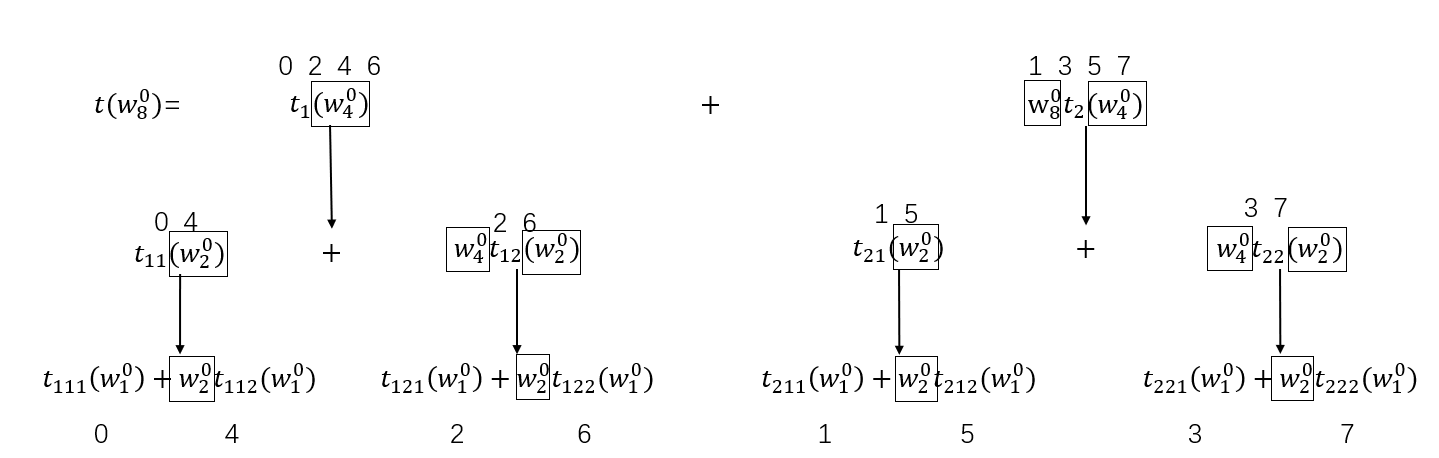
- 每个公示的上面的数字表示的是当前多项式的系数
- 如果当求解的数值变成了\(w_8^k\),只需要对每个黑框中的数值进行相应的替换
如果考虑到不同的\(w_8^k\)的求解,那么上面的求解过程实际上是在下面的表中遍历了一棵二叉树
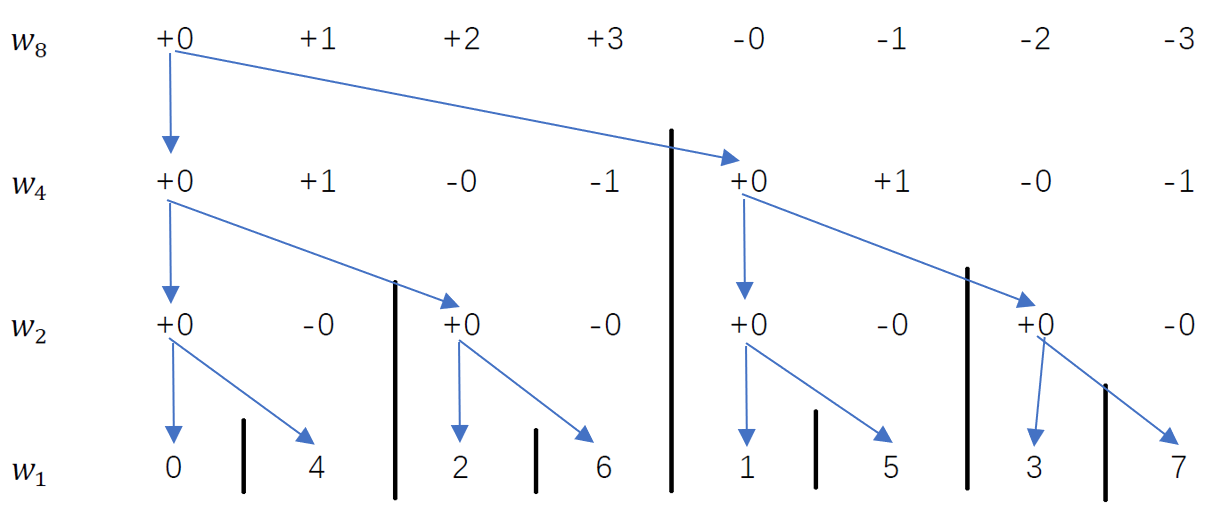
- 第一个\(+0\)表示的是左边的分支(\(t_1(w_4^0)\)) ,加上(也就是”+“的意思)\(w_8^0\)(“0”代表的是右上标)乘上右边的分支(\(t_2(w_4^0)\))。
- 由于两个关于原点对称的单位复数的符号相反,所以后一部分第二项前面乘的系数可以\(+w_8^{4+k}\)写成\(-w_8^k\)(简写成为“\(-k\)")
- 中间的黑色竖杠将区间在不同深度上分成了不相交的子区间
下面是几种情况的求解过程,可以理解下
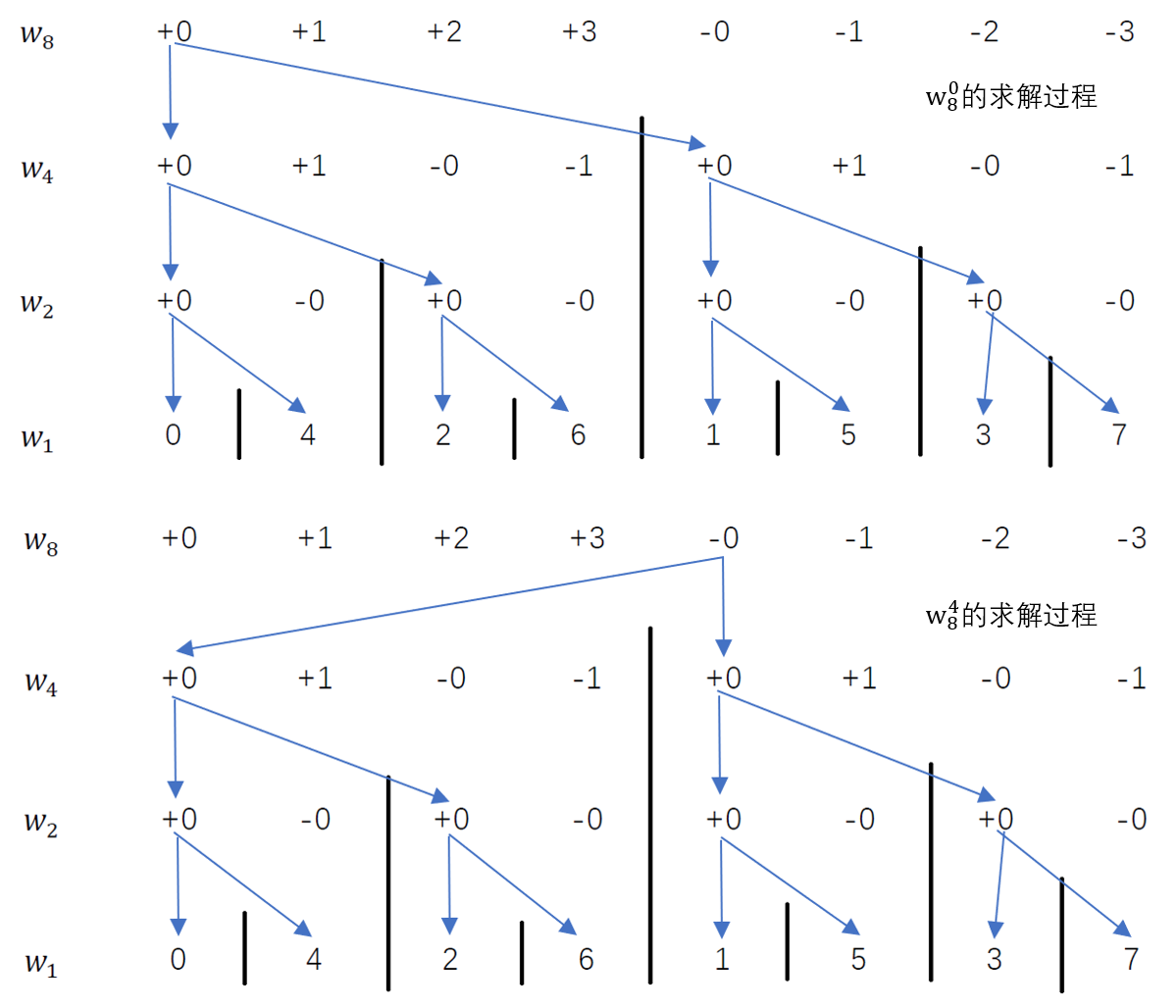

可以看出所有的多项式的求解都是在这个\(4\times8\)的表格上进行的,从下到上维护整个表格便可以得到傅里叶变换,每一层维护的时间复杂度是\(O(n)\),从\(w_2\)到\(w_8\)一共三层(每层都是类似开方的降系数),所以层数是\(O(logn)\),因此总的时间复杂度是\(O(nlogn)\)
傅里叶变化的优化实际上利用\(w_{2r}^{2k}=w_r^k\) 这个性质,巧妙的将计算的复杂度降了下来。如果递归求解,实际上也是要递归到最后一层,将该层的信息整体维护好供上层使用。
逆傅里叶变换(IFFT)(最近有点忙,有时间再看)未完待续。。。。
模板:
代码的一些细节,比如rev[i]的作用和如何实现的,可以参考别人的文章。
#include <cmath>
#include <complex>
using namespace std;
typedef complex<double> cpx;
const double pi = acos(-1.0);
int rev[maxn];
void fft_init(cpx *coe1, cpx *coe2, int n, int &bit, int &bit_len) {
bit = 0;
while ((1<<bit) < n) bit++;
bit_len = 1<<bit; // 找到最小的2的幂次方数
for (int i = 0; i < bit_len; i++) coe1[i] = coe2[i] = 0;
for (int i = 0; i < bit_len; i++) //初始化每个元素对应的最后的位置
rev[i] = (rev[i>>1]>>1) | ((i&1)<<(bit-1));
}
void fft(cpx *coe, int bitn, int bit, int inv) {
for (int i = 0; i < bitn; i++)
if (i < rev[i]) swap(coe[i], coe[rev[i]]);
// mid枚举隔板的长度
for (int mid = 1; mid < bitn; mid <<= 1) {
cpx tmp(cos(pi/double(mid)), inv*sin(pi/mid));
// 枚举当前在哪一个隔板那里
for (int i = 0; i < bitn; i += (mid<<1)) {
cpx omega(1.0, 0.0);
// 计算两边函数的值,隔板的左边是x+y,隔板右边是x-y
for (int j = 0; j < mid; j++, omega *= tmp) {
cpx x = coe[i + j], y = omega*coe[i+j+mid];
coe[i+j] = x + y, coe[i+j+mid] = x - y;
}
}
}
// 逆映射
if (inv < 0) for (int i = 0; i < bitn; i++) coe[i] /= double(bitn);
}


