最长公共子序列

 

很久之前就有研究这个算法

结果忘记上传了     哈哈

前天看到好多同学需要这个算法   

所以 来吧   写一写

 

先来看下  什么是公共子序列    

我直接来一张图 相信大家就明白了     当然  图片是百度到的 

 

 

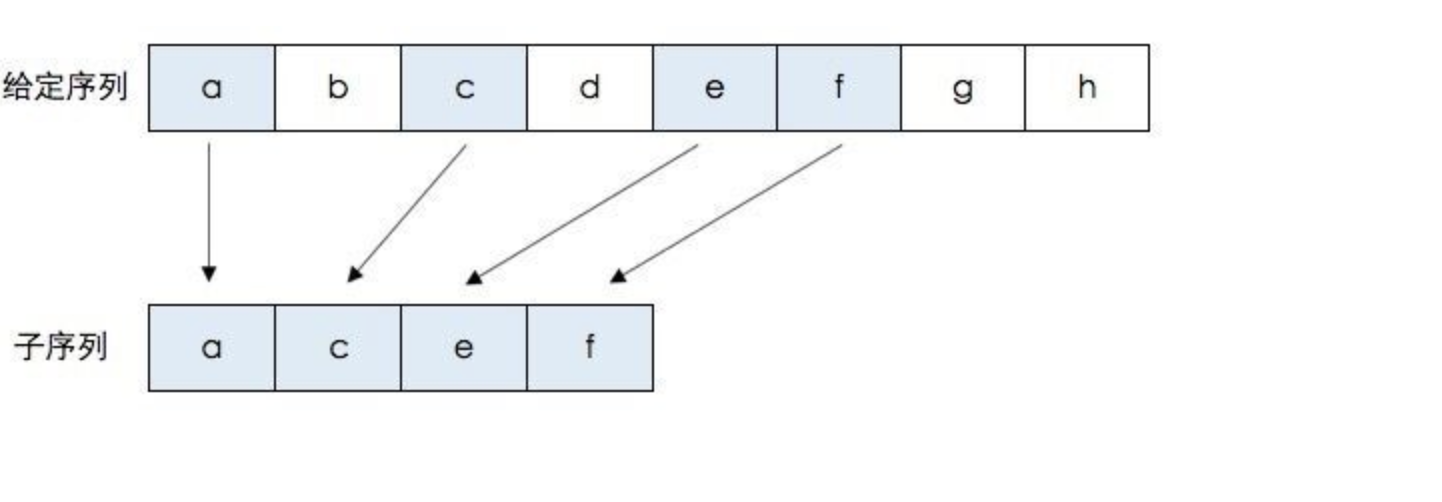
 涂色部分就是  公共子序列   

 

 

OK  相信到这里 大家对什么是子序列    有了一定的概念     

记住  子序列和  子串不是同一个概念

那么  我们今天的问题就来了  

最长的公共子序列   怎么来找呢   

是不是有点懵

 

废话不说  

先上代码

 

 

//

//  main.c

//  most

//

//  Created by 陈昌明 on 2020/4/11.

//  Copyright © 2020 陈昌明. All rights reserved.

//

 

#include<stdio.h>

#include<stdlib.h>

#include<string.h>

int aa,bb;//记录长度

int max(int a,int b)

{

    if(a>b)

    {

        return a;

    }

    return b;

}

int Max(char a[],char b[])

{

    int M=0;

    int n1=(int)strlen(a);

    int n2=(int)strlen(b);

    if(n1>0 && n2>0)

    {

        if(*a==*b)

        {

            M=1+Max(++a,b);

        }

        else

        {

            if((n1>=1 && n1>=0) || (n2>=1 && n2>=0) )//是否还能继续 当然 也是结束条件

            M=M+max(Max(a+1,b),Max(a,b+1));//动态规划

        }

    }

    return M;

}

int main()

{

    char a[100];

    char b[100];

    scanf("%s",a);

    scanf("%s",b);

    aa=(int)strlen(a);

    bb=(int)strlen(b);

    int Mmax=Max(a,b);

    printf("%d\n",Mmax);

    return 0;

}

 

 

这个版本应该是通用的 

前面由于编译器的问题   转型有点问题  

现在已近改进    应该可以适应所有的编译器

 

 

OK   少说废话  

来讲题 

 

 

为了方便大家理解  

我去拷贝了 大佬总结的公式    

 

 

 

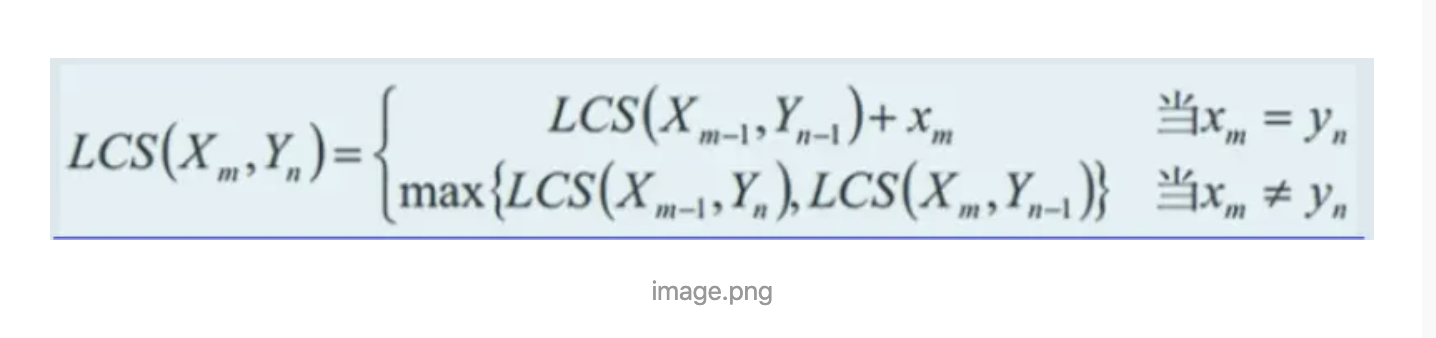
现在我们来过一遍这个公式   型芯大家就有点了解了

 

我们只讲动态规划的一节  因为节节都是同一个道理 

X Y  为两个字符串    m  n   分别指长度

 

就是  当两个字符串的当前字符相同时  同时 移动一位 然后得到的结果即长度相加

当当前的两个不同时   就要考虑 第一个字符串移动后一个不移动 和反过来的两种情况的最大值

 

OK  现在思路应该明白      不明白的再去悟悟公式   可以随便弄几个简单的字符串试验一下   

 

当然上面的代码自身  输出的长度   

其实也是可以得到字符串的

这里就不实现了 

 

不过建议用java 试着实现以下    （java 的话会方便一丢丢  个人感觉）

 

OK 今天就到这

谢谢大家