全排列的详细解析

好久没有更新了，今天来更新一下。
今天来说一下关于全排列的问题
那么第一个问题，什么是全排列？
全排列可以理解为，数学里面的排列组合
更简单的说呢，就是，从一到n这n个数有多少种排列情况？
当然，答案显而易见，就是:  n的阶乘当然，n的阶乘肯定不是今天要讨论的东西

 

今天我们要讨论的就是如何把这n的阶乘种情况给表示出来
那么下面我们切入正题开始分析如何生成全排列？
我们先看第一位的情况，他有n个数，从一到n那么开头的情况肯定是n种，123直到n
当然，因为开头是1，所以一的时候就不用多说，对吧？
然后下面就要分出2开头，3开头到n开头的情况，对吧？那么怎么生成这种情况呢？就是拿1和2和3和4到n依次换位（1开头可以理解为1和自己交换）
这样第一位的情况就考虑完了，对吧？下面我们考虑第二位，第二位其实也是这样，考虑第二位自己不变，第二位和后面的换和(后面的后面)的换....
更直接的说就是第一位已经确定假设是1，后面还有n-1个数，第二位可能是2，可能是3，可能是....n，那么久，等同于拿2和自己换位和3换位和4换位到和n换位
那么，我这样往下分析下去，直到就是说第n-1位和第一个n位换位。下面就没有分叉了  
意思就是说我们要在，第一位不换位的情况下去考虑，用第二位和自己换位和第三位和第四位，直到第n位，这些情况，然后再这些情况的每一种情况下再去考虑分叉出的情况，依次往下，直到考虑到第n-1位和，第n位换位
因为每一种情况下面都会分出各种情况，而各种情况之后，又会分出各种情况，那么，我们再具体说些细节问题

也就是说，考虑到某一种情况，一直往下延伸，直到无法往下延伸的某一种情况的时候，也就是说，对n-1为和dn位换位之后，此时我们会生成一个新的排列，这就是全排列中的一种情况，由于我们生成此排列的时候，对dny和an-1为进行了换位，由于我们要保证生成其他排列时，他们的顺序和本序列生成所面对的序列情况相同，我们输出这个新的排列，也就是刚才我们所说的一个排列突出之后呢，我们要把它换回来，这里称之为，回朔

这样才能保证全排列的全

OK    

下面我们来看代码

这里用Java来编码

import java.util.Scanner;

public class Permutation {


  public static int count = 0;

  public static void main(String[] argv) {

    Scanner in =new Scanner(System.in);
    int N = in.nextInt();//输入N   这里用于输出1到N的全排列
    int[] key = new int[N];
    for(int i=0;i<key.length;i++){
      key[i]=i+1;
    }
    check(0,key,N);
  }
  public static void check(int n,int[] a,int N){//换位函数
    int i;
    if(n==N){//符合条件输出
      Put(a);
    }
    for(i=n;i<N;i++){
      int x=a[n];
      a[n]=a[i];
      a[i]=x;
      check(n+1,a,N);//考虑下面分叉
      x=a[n];
      a[n]=a[i];//回溯
      a[i]=x;
    }
  }
  public static void Put(int[] a){//输出函数
    int i;
    for (i=0;i<a.length;i++){
      System.out.print(a[i]+" ");
    }
    System.out.println();
  }
}

上面就是代码

下面我们看示例输出

 

 

 

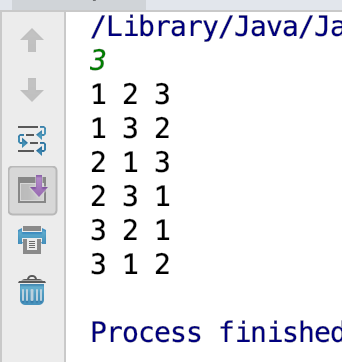
太大的数呢

输出太长

就不展示了

主要是理解这个思路

因为很多算法题明里暗里都会用到全排列的计算

OK   这次更新就到这