有向图的强连通分量(转)

---恢复内容开始---

引自：   http://www.cnblogs.com/luweiseu/archive/2012/07/14/2591370.html

Kosaraju算法

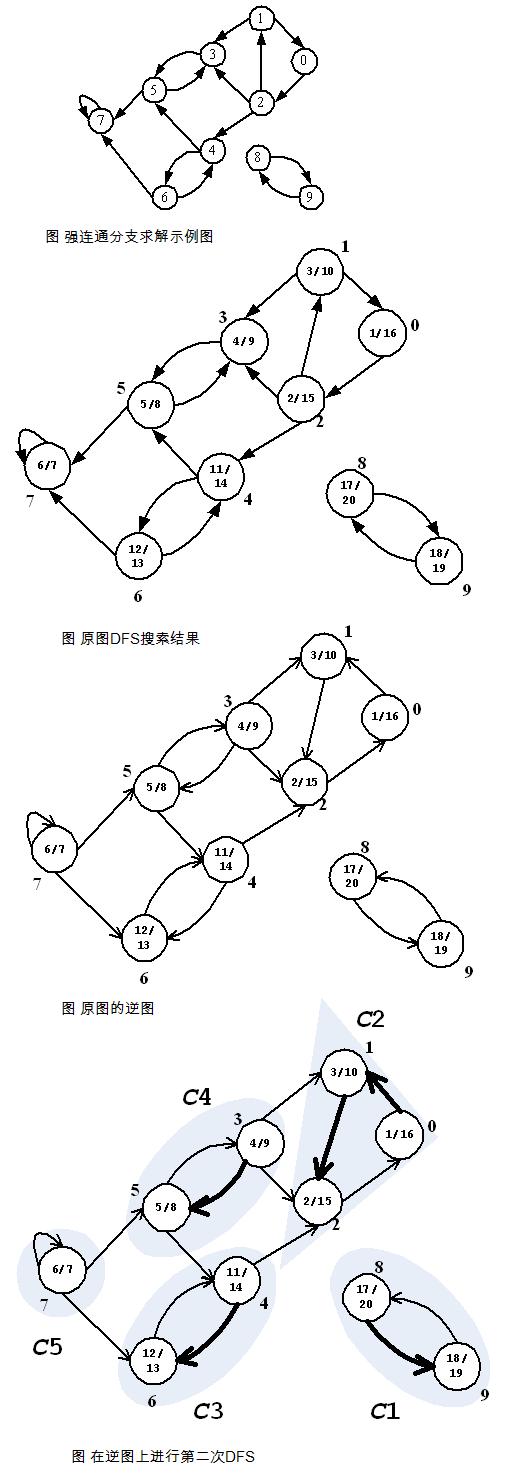
Kosaraju算法的解释和实现都比较简单，为了找到强连通分支，首先对图G运行DFS，计算出各顶点完成搜索的时间f；然后计算图的逆图GT，对逆图也进行DFS搜索，但是这里搜索时顶点的访问次序不是按照顶点标号的大小，而是按照各顶点f值由大到小的顺序；逆图DFS所得到的森林即对应连通区域。具体流程如图(1~4)。

上面我们提及原图G的逆图GT，其定义为GT=(V, ET)，ET={(u, v):(v, u)∈E}}。也就是说GT是由G中的边反向所组成的，通常也称之为图G的转置。在这里值得一提的是，逆图GT和原图G有着完全相同的连通分支，也就说，如果顶点s和t在G中是互达的，当且仅当s和t在GT中也是互达的。

 

 

Tarjan算法

Kosaraju算法的流程简单，但是需要对图(和逆图)进行两次DFS搜索，而且读逆图的DFS搜索中顶点的访问顺序有特定的限制。下面将介绍的两个算法的过程比Kosaraju算法更为简洁，只需要执行一次DFS，并且不需要计算逆图。

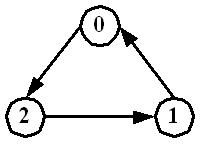
Tarjan基于递 归实现的深度优先搜索，在搜索过程中将顶点不断压入堆栈中，并在回溯时判断堆栈中顶点是否在同一联通分支。函数借助两个辅助数组pre和low，其中 pre[u]为顶点u搜索的次序编号，low[u]为顶点u能回溯到的最早的顶点的次序编号。当pre[u]=low[u]时，则弹出栈中顶点并构成一个 连通分支。以一个简单的例子来解释这一过程，如图所示，

 

	递归				回溯
栈	0	2	1
顶点	0	2	1	0	1	2	0
pre	0	1	2		2	1	0
low	0	1	2		0	0	0

寻找图中连通分支的过程

 

对图中的简单联通图，首先递归地对图进行深度优先搜索，并记录每个顶点的搜索次序pre。搜索起点为0，当对顶点1进行递归时将再次达到顶点0；在回溯过程中依次将顶点1和顶点2的low值修改为low[0]。当回溯到顶点0时将栈中low值为low[0]的顶点弹出并组成一个连通分支。

Tarjan算法 
pre[u]表示u结点的访问时间，low[u]表示u以及u的后代能访问到的最早的最先结点v的pre[v]
如果pre[u] == low[v]，则说明u是DFS树中u所在SCC的起始点，这时u之后栈内的结点都是u所在SCC中的结点，将它们出栈并染色
计算low[u]的方法和无向图求割顶割边时类似
(u, v) in E
若v未被访问，即(u, v)为树枝边，low[u] = min(low[u], low[v])
若v已被访问，如果v在栈中，(u, v)可以为后向边也可以为连接同一个DFS树中没有后代关系的两个结点的交叉边，
                       low[u] = min(low[u], pre[v])
                       如果v不在栈中，(u, v)为连接不同DFS树的交叉边，v处于另一个SCC，不必考虑