Z-buffer算法
1、Z缓冲区(Z-Buffer)算法
1973年,犹他大学学生艾德·卡姆尔(Edwin Catmull)独 立开发出了能跟踪屏幕上每个像素深度的算法 Z-buffer
Z-buffer让计算机生成复杂图形成为可能。Ed Catmull目 前担任迪士尼动画和皮克斯动画工作室的总裁
Z缓冲器算法也叫深度缓冲器算法,属于图像空间消隐算法
该算法有帧缓冲器和深度缓冲器。对应两个数组:
intensity(x,y)——属性数组(帧缓冲器)
存储图像空间每个可见像素的光强或颜色
depth(x,y)——深度数组(z-buffer)
存放图像空间每个可见像素的z坐标

假定xoy面为投影面,z轴为 观察方向
过屏幕上任意像素点(x,y) 作平行于z轴的射线R,与物 体表面相交于p1和p 2 点
p1和p 2点的z值称为该点的深 度值
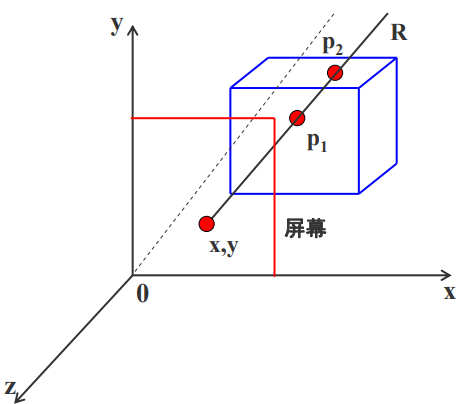
z-buffer算法比较p1和p 2的z值, 将最大的z值存入z缓冲器中
显然,p1在p 2前面,屏幕上(x,y) 这一点将显示p1点的颜色
算法思想:先将Z缓冲器中各单元的初始值置为最小值。
当 要改变某个像素的颜色值时,首先检查当前多边形的深度值是否大于该像素原来的深度值(保存在该像素所对应的Z 缓冲器的单元中)
如果大于原来的z值,说明当前多边形更靠近观察点,用它的颜色替换像素原来的颜色
Z-Buffer算法()
{
帧缓存全置为背景色
深度缓存全置为最小z值
for(每一个多边形)
{
扫描转换该多边形
for(该多边形所覆盖的每个象素(x,y) )
{
计算该多边形在该象素的深度值Z(x,y);
if(z(x,y)大于z缓存在(x,y)的值)
{
把z(x,y)存入z缓存中(x,y)处
把多边形在(x,y)处的颜色值存入帧缓存的(x,y)处
}
}
}
}
z-Buffer算法的优点:
(1)Z-Buffer算法比较简单,也很直观
(2)在象素级上以近物取代远物。与物体在屏幕上的出现 顺序是无关紧要的,有利于硬件实现
z-Buffer算法的缺点:
(1)占用空间大
(2)没有利用图形的相关性与连续性,这是z-buffer算法 的严重缺陷
(3)更为严重的是,该算法是在像素级上的消隐算法
2、只用一个深度缓存变量zb的改进算法
一般认为,z-Buffer算法需要开一个与图象大小相等的缓 存数组ZB,实际上,可以改进算法,只用一个深度缓存变 量zb
z-Buffer算法()
{ 帧缓存全置为背景色
for(屏幕上的每个象素(i,j))
{ 深度缓存变量zb置最小值MinValue
for(多面体上的每个多边形Pk)
{
if(象素点(i,j)在pk的投影多边形之内)
{
计算Pk在(i,j)处的深度值depth;
if(depth大于zb)
{ zb = depth;
indexp = k;(记录多边形的序号)
}
}
}
If(zb != MinValue) 计算多边形Pindexp在交点 (I,j) 处的光照
颜色并显示
}
}
关键问题:判断象素点(i,j)是否在pk的投影多边形之内, 不是一件容易的事。节省了空间但牺牲了时间。
计算机的很多问题就是在时间和空间上找平衡
另一个问题计算多边形Pk在点(i,j)处的深度。设多边 形Pk的平面方程为:
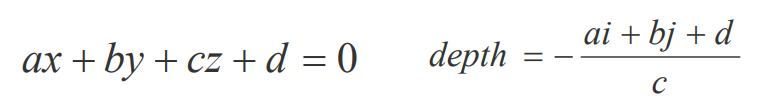
点与多边形的包含性检测:
(1)射线法
由被测点P处向 y = -∞方 向作射线
交点个数是奇数,则被测点在 多边形内部
交点个数是偶数表示在多边形外部

若射线正好经过多边形的顶点,则 采用“左开右闭”的原则来实现
即:当射线与某条边的顶点相交 时,若边在射线的左侧,交点有 效,计数;若边在射线的右侧, 交点无效,不计数
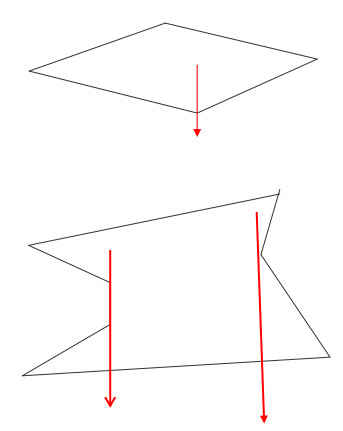
用射线法来判断一个点是否在多边形内的弊端:
(1)计算量大
(2)不稳定
(2)弧长法
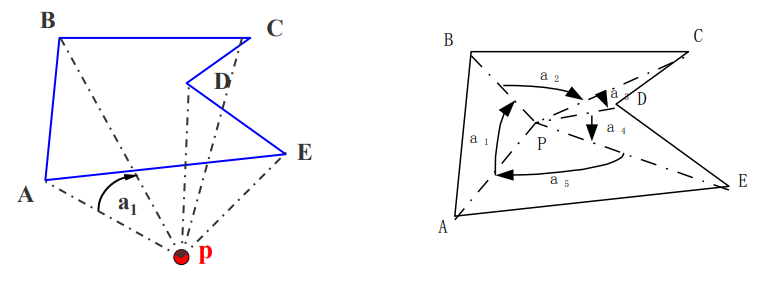
以p点为圆心,作单位圆,把边投影到单位圆上,对应一段段 弧长,规定逆时针为正,顺时针为负,计算弧长代数和
代数和为0,点在多边形外部
代数和为2π,点在多边形内部
代数和为π,点在多边形边上
这个算法为什么是稳定的?
假如算出来后代数和不是0,而 是0.2或0.1,
那么基本上可以断定这个点在外部,可以认为 是有计算误差引起的,实际上是0。
但这个算法效率也不高,问题是算弧长并不容易,
因此又 派生出一个新的方法—以顶点符号为基础的弧长累加方法
(3)以顶点符号为基础的弧长累加方法
p是被测点,按照弧长法,p点 的代数和为2π
不要计算角度,做一个规定来 取代原来的弧长计算


同一个象限认为是 0,跨过一个象限是 π/2,跨过二个象限 是 π。
这样当要计算代数和的时候,就不要去投影了,
只 要根据点所在的象限一下子就判断出多少度,这样几乎没 有什么计算量,只有一些简单的判断,效率非常高
小结
z-buffer算法是非常经典和重要的,在图形加速卡和固件 里都有。
只用一个深度缓存变量zb的改进算法虽然减少了 空间,但仍然没考虑相关性和连贯性



