多边形裁剪

一、多边形的裁剪

如果按线段的方法裁剪，得到的是一系列线段。

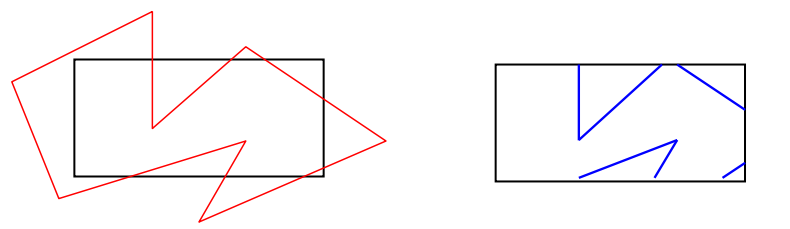
而实际上，应该得到的是下图所示的有边界的区域：

多边形裁剪算法的输出应该是裁剪后的多边 形边界的顶点序列！

需要构造能产生一个或多个封闭区域的多边 形裁剪算法

二、Sutherland-Hodgeman多边形裁剪

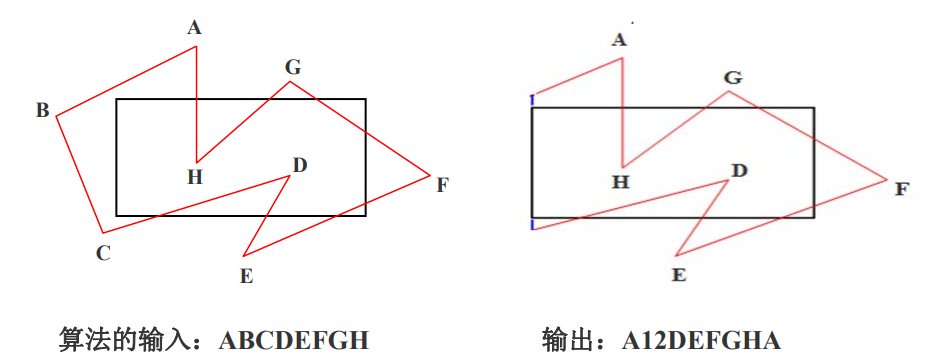
该算法的基本思想是将多边形边界作为一个整体，

每次用窗口的一条边对要裁剪的多边形和中间结果多边形进行裁剪，

体现一种分而治之的思想

把平面分为两个区域：

包含有窗口区域的一个域称为可见侧；

不包含窗口区域的域为不可见侧

 

裁剪得到的结果多边形的顶点有两部分组成：

（1）落在可见一侧的原多边形顶点

（2）多边形的边与裁剪窗口边界的交点

根据多边形每一边与窗口边所形成的位置关系，沿着多边形 依次处理顶点会遇到四种情况：

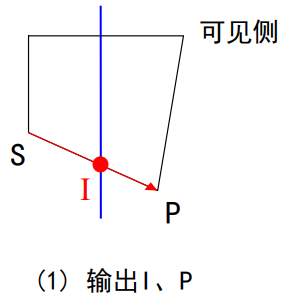
（1）第一点S在不可见  侧面，而第二点P在 可见侧

交点I与点 P均被加入到输 出顶点表中。

 

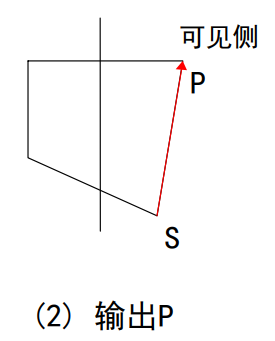
（2）是S和P都在可见侧

 则P被加入到输出顶点表中

（3）S在可见侧，而P在不可见侧

则交点I被加入到输出顶点表中

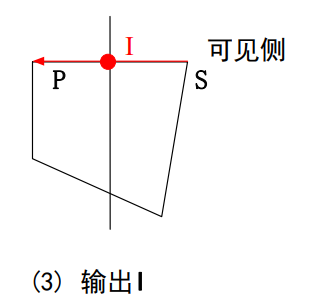
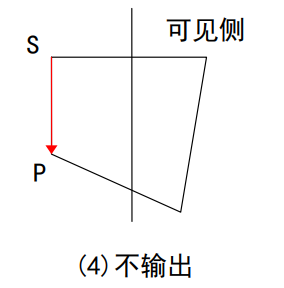
（4）如果S和P都在不可见侧

输出顶点表中不增加任何顶点

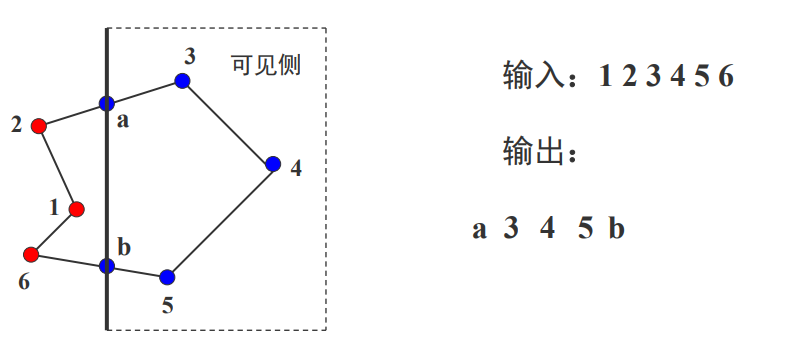
在窗口的一条裁剪边界处理完所有顶 点后，其输出顶点表将用窗口的下一 条边界继续裁剪

 

 

 

while对于每一个窗口边或面 do

　　begin

　　　　if P1 在窗口边的可见一侧 then 输出P1

　　　　for i=1 to n do

　　　　begin

 　　　　if P1 在窗口边的可见一侧 then

　　　　if P1+1 在窗口边的可见一侧 then 输出 P1+1

 　　　　else 计算交点并输出交点

　　　　else if Pi+1 在窗口可见一侧，then 计算交点

　　　　　　并输出交点，同时输出Pi+1

　　　　end

　　end

end

 

Sutherland-Hodgeman算法不足之处

利用Sutherland-Hodgeman裁剪算法对凸多边形进行裁剪可以 获得正确的裁剪结果，但是凹多边形不行。