LCA 的理解(转载)
LCA的tarjan算法的理解
tarjan算法的步骤是(当dfs到节点u时):
1 在并查集中建立仅有u的集合,设置该集合的祖先为u
1 对u的每个孩子v:
1.1 tarjan
1.2 合并v到父节点u的集合,确保集合的祖先是u
2 设置u为已遍历
3 处理关于u的查询,若查询(u,v)中的v已遍历过,则LCA(u,v)=v所在的集合的祖先
举例说明(非证明):
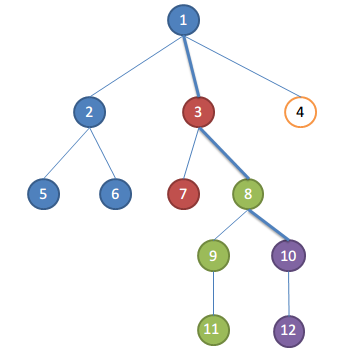
假设遍历完10的孩子,要处理关于10的请求了
取根节点到当前正在遍历的节点的路径为关键路径,即1-3-8-10
集合的祖先便是关键路径上距离集合最近的点
比如此时:
1,2,5,6为一个集合,祖先为1,集合中的点和点10的LCA为1
3,7为一个集合,祖先为3,集合中的点和点10的LCA为3
8,9,11为一个集合,祖先为8,集合中的点和点10的LCA为8
10,12为一个集合,祖先为10,集合中的点和点10的LCA为10
你看,集合的祖先便是LCA吧,所以第3步是正确的
道理很简单,LCA(u,v)便是根至u的路径上到节点v最近的点
此题为POJ 3694
1 #include<iostream> 2 #include<algorithm> 3 #include<vector> 4 #include<stdio.h> 5 #include<stdlib.h> 6 #include<string.h> 7 using namespace std; 8 #define maxn 102000 9 vector<vector<int> >G; 10 int low[maxn],dfn[maxn],father[maxn],bridge[maxn],ans; 11 int n,m,q,t; 12 void Init() 13 { 14 G.clear(); 15 G.resize(n+1); 16 memset(father,-1,sizeof(father)); 17 memset(low,0,sizeof(low)); 18 memset(dfn,0,sizeof(dfn)); 19 memset(bridge,0,sizeof(bridge)); 20 t=1,ans=0; 21 } 22 void Tarjan(int u,int fa) 23 { 24 low[u]=dfn[u]=t++; 25 father[u]=fa; 26 int len=G[u].size(),v; 27 for(int i=0; i<len; i++) 28 { 29 v=G[u][i]; 30 if(!low[v]) 31 { 32 Tarjan(v,u); 33 low[u]=min(low[u],low[v]); 34 if(dfn[u] < low[v]) 35 { 36 ans++; 37 bridge[v]=1; 38 } 39 } 40 else if(fa!= v) 41 low[u] =min(low[u],dfn[v]); 42 } 43 } 44 void LCA(int u,int v) 45 { 46 if(u==v) return ; 47 if(dfn[u] > dfn[v]) 48 { 49 if(bridge[u] == 1) 50 { 51 bridge[u]=0; 52 ans--; 53 } 54 LCA(father[u],v); 55 } 56 else 57 { 58 if(bridge[v] == 1) 59 { 60 bridge[v]=0; 61 ans--; 62 } 63 LCA(u,father[v]); 64 } 65 } 66 int main() 67 { 68 int a,b,i=0; 69 while(scanf("%d%d",&n,&m),n+m) 70 { 71 i++; 72 Init(); 73 while(m--) 74 { 75 scanf("%d%d",&a,&b); 76 G[a].push_back(b); 77 G[b].push_back(a); 78 } 79 printf("Case %d:\n",i); 80 Tarjan(1,0); 81 scanf("%d",&q); 82 while(q--) 83 { 84 scanf("%d%d",&a,&b); 85 LCA(a,b); 86 printf("%d\n",ans); 87 } 88 } 89 return 0; 90 }




