Codeforces Round #514 (Div. 2) D. Nature Reserve 多个二次函数的最大值是三分函数的证明
http://codeforces.com/contest/1059/problem/D
最大值：
最左下方和最右下方分别有一个点
r^2 - (r-1)^2 = (10^7)^2
maxr<0.5*10^14
Way1:
二分。
difference:
如果使用 5*10^13 -> 10^-6，2^ 60~70区间，pow,sqrt运算，实测超时。
实际上是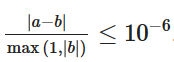
，使用
。
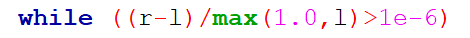time of a case：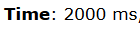
->
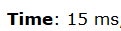
Code：
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int maxn=1e5+10; 4 5 double x[maxn],y[maxn]; 6 double z=5.0*1e13; 7 int n; 8 9 bool work(double m) 10 { 11 double p,q,d; 12 int i; 13 p=-z; q=z; 14 for (i=1;i<=n;i++) 15 { 16 d=sqrt(pow(m,2)-pow(m-y[i],2)); 17 p=max(p,x[i]-d); 18 q=min(q,x[i]+d); 19 // if (p>q) 20 // return 0; 21 } 22 // return 1; 23 if (p<=q) 24 return 1; 25 else 26 return 0; 27 } 28 29 int main() 30 { 31 double l=0,r,m; 32 int v,i; 33 scanf("%d",&n); 34 v=0; 35 for (i=1;i<=n;i++) 36 { 37 scanf("%lf%lf",&x[i],&y[i]); 38 if (y[i]!=0) 39 { 40 if (v==0) 41 v=(y[i]>0); 42 else if (v!=(y[i]>0)) 43 { 44 printf("-1"); 45 return 0; 46 } 47 } 48 y[i]=fabs(y[i]); 49 l=max(l,y[i]/2); 50 } 51 r=z; 52 while ((r-l)/max(1.0,l)>1e-6) 53 { 54 m=(l+r)/2; 55 if (work(m)) 56 r=m; 57 else 58 l=m; 59 } 60 printf("%.10f",r); 61 return 0; 62 }
Way2:
多个二次函数f1,f2,…,fn，ax^2+bx+c (a>0)
f(x)=max(f1(x),f2(x),…,fn(x))，
而f是先减小，后增大，使用三分法
证明：
设f(x)是由多个连续的二次函数片段组成，相邻的二次函数片段的斜率逐渐增大，而每个二次函数片段都是f''>0，所以当前f''>0
设加入新的函数后，变化的区间为
1.[d1,d2]，新的函数的片段替代原来的部分，满足f'‘’>0，且新的函数的片段往d1外，点外延伸，比原来的数值小，满足f'(d1-delta)<f'(d1+delta),f'(d2-delta)<f'(d2+delta)
2.(-inf,d1],[d1,inf）同理。
1 #include <bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 #define minv 1e-6 5 #define inf 1e9 6 #define pi 3.1415926536 7 #define nl 2.7182818284 8 const ll mod=1e9+7;//998244353 9 const int maxn=1e5+10; 10 11 int a[maxn],b[maxn],x[maxn],y[maxn],n; 12 double u[maxn],v[maxn],w[maxn]; 13 14 double f(double m) 15 { 16 double mm,z=0; 17 int i; 18 mm=m*m; 19 for (i=1;i<=n;i++) 20 z=max(z,u[i]*mm+v[i]*m+w[i]); 21 return z; 22 } 23 24 int main() 25 { 26 int cond=0,i; 27 double l,r,m,mm,a,b; 28 scanf("%d",&n); 29 for (i=1;i<=n;i++) 30 { 31 scanf("%d%d",&x[i],&y[i]); 32 if (y[i]!=0) 33 { 34 if (cond==0) 35 cond=(y[i]>0); 36 else if (cond!=(y[i]>0)) 37 { 38 printf("-1"); 39 return 0; 40 } 41 } 42 y[i]=abs(y[i]); 43 u[i]=0.5/y[i]; 44 v[i]=-1.0*x[i]/y[i]; 45 w[i]=(1.0*x[i]*x[i]+1.0*y[i]*y[i])/2/y[i]; 46 } 47 l=-1.0e7,r=1.0e7; 48 while (1) 49 { 50 m=(l+r)/2; 51 mm=(m+r)/2; 52 a=f(m); 53 b=f(mm); 54 if (fabs(a-b)/max(1.0,min(a,b))<1e-8) 55 break; 56 if (f(mm)>f(m)) 57 r=mm; 58 else 59 l=m; 60 } 61 printf("%.10f",a); 62 return 0; 63 }
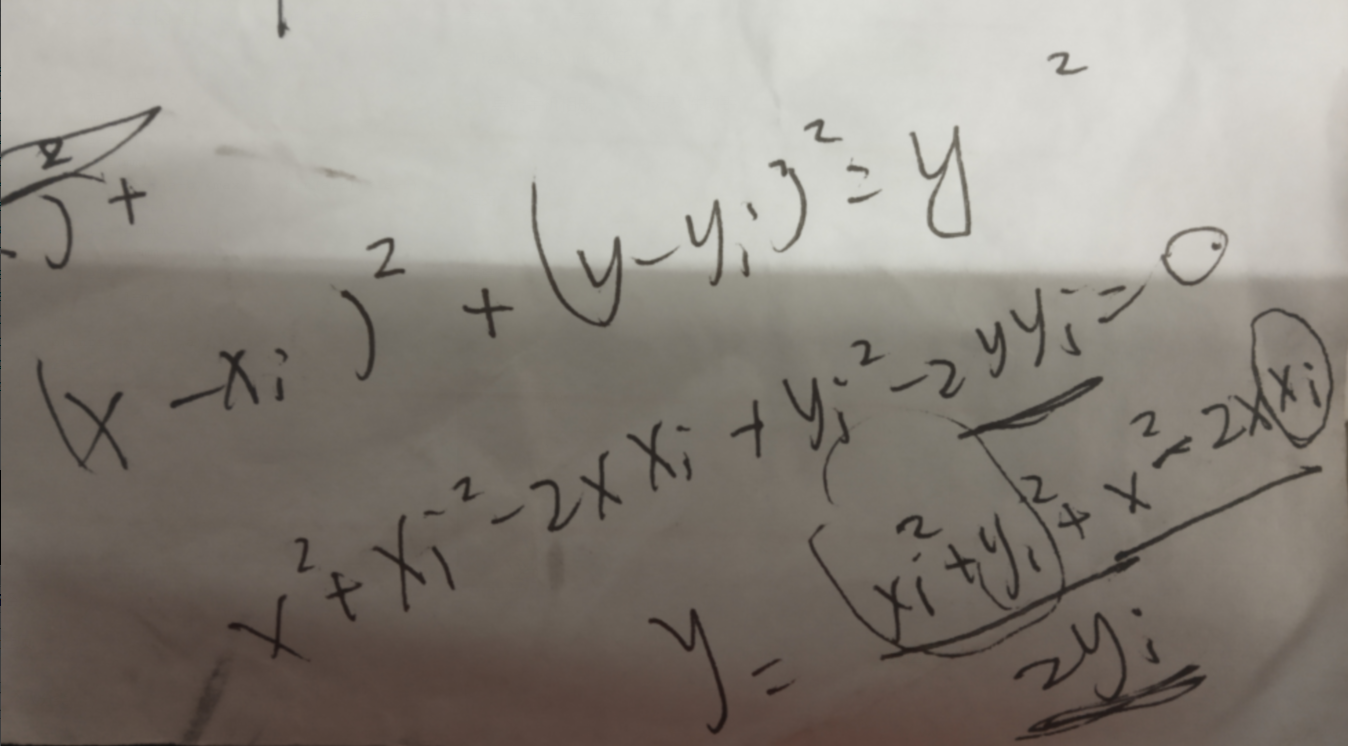
类似：
hdu4717 The Moving Points
