2018蓝桥杯省赛一些有趣的题目 及 未证明极简略题解
看了一下C/C++ B组、Java的题,发现掉坑了……
1. 明码
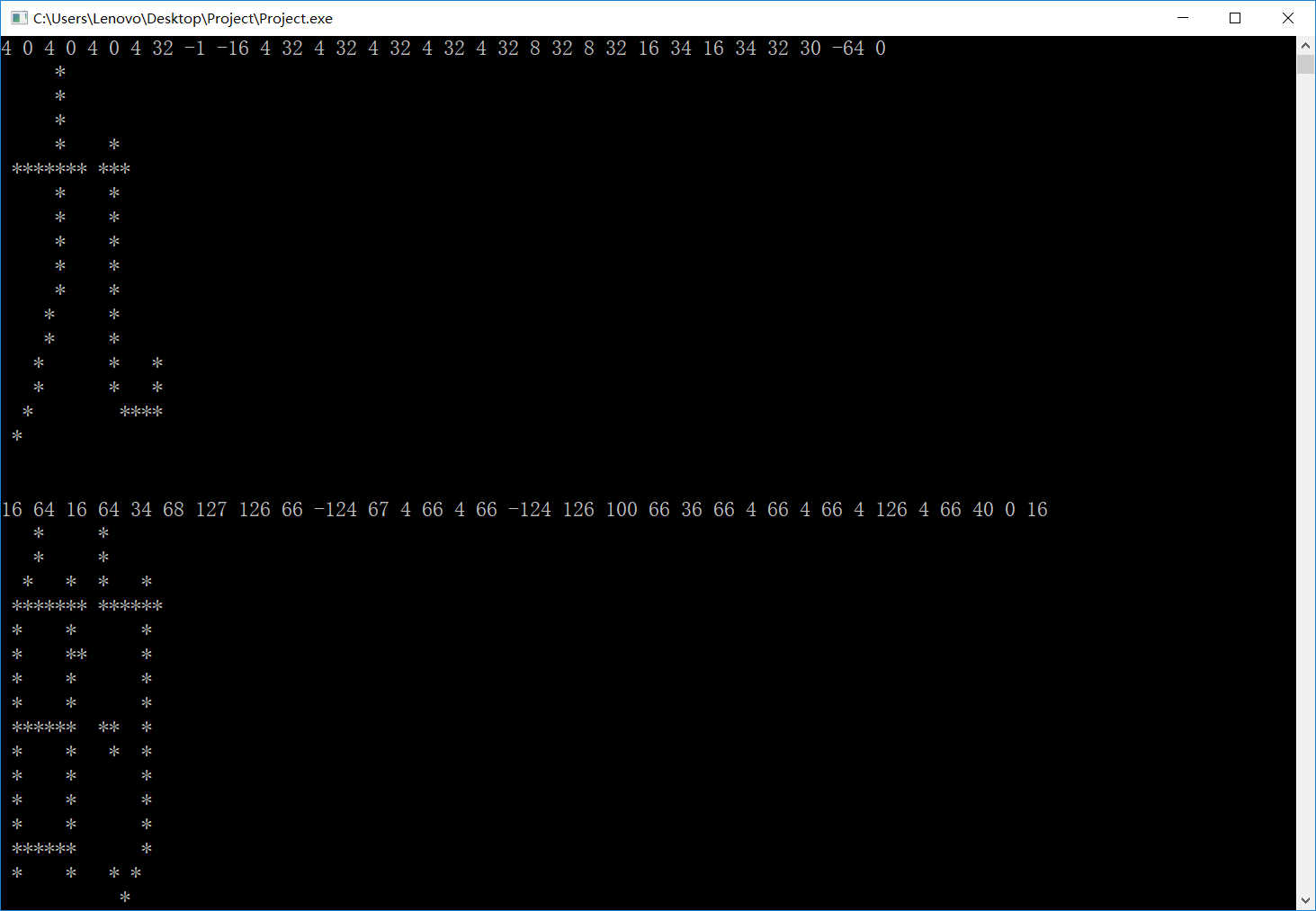
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cstring> 4 #include <cmath> 5 #include <list> 6 #include <stack> 7 #include <vector> 8 #include <set> 9 #include <map> 10 #include <queue> 11 #include <algorithm> 12 #include <iostream> 13 using namespace std; 14 15 char str[16][16]; 16 17 int main() 18 { 19 long i,j,k,a,b; 20 for (k=1;k<=10;k++) 21 { 22 for (i=0;i<16;i++) 23 { 24 scanf("%ld%ld",&a,&b); 25 // a+=128; b+=128; 26 if (a<0) 27 a+=128; 28 if (b<0) 29 b+=128; 30 for (j=7;j>=0;j--) 31 str[i][7-j]=(a>>j) & 1; 32 for (j=7;j>=0;j--) 33 str[i][15-j]=(b>>j) & 1; 34 } 35 for (i=0;i<16;i++) 36 { 37 for (j=0;j<16;j++) 38 if (str[i][j]==1) 39 printf("*"); 40 else 41 printf(" "); 42 printf("\n"); 43 } 44 printf("\n\n"); 45 } 46 printf("%ld",pow(9,9)); 47 return 0; 48 }
2. 测试次数
我一开始想错了,这是错误代码
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cstring> 4 #include <cmath> 5 #include <list> 6 #include <stack> 7 #include <vector> 8 #include <set> 9 #include <map> 10 #include <queue> 11 #include <algorithm> 12 #include <iostream> 13 using namespace std; 14 15 //[0,1000] 16 //判断一个数k,<k or >=k 17 //[x,y]判断(x+y+1)/2,而不是 (x+y)/2 18 //对于x+y+1为奇数的情况,结果>=k的情况最糟,如[1,3] -> [2,3] 19 20 //n=1000为最糟糕的情况 21 22 int main() 23 { 24 long l,r,mid,t=0; 25 l=0; r=1000; 26 while (l<=r) 27 { 28 l=(l+r+1)/2; 29 t++; 30 if (l==1000) 31 break; 32 } 33 printf("%ld",t); 34 return 0; 35 }
没有注意到:抽样3部手机参加测试。
http://blog.sina.com.cn/s/blog_3fe961ae0101llmf.html
https://blog.csdn.net/clx55555/article/details/79855677
另,未证明极简略题解:
C/C++ A组:
航班时间 模拟,创建多几组测试数据
三体攻击 不会ac解,骗骗分还是会的,有大神说是线段树(记录每一段的最小值)+前缀和(不懂)
比赛的时候搞了一个一维数组,贼复杂,其实这样就可以了:
1 long n,m,p; 2 scanf("%ld%ld%ld",&n,&m,&p); 3 long a[n][m][p]; 4 a[0][0][0]=1; a[1][0][0]=2; a[2][0][0]=3; 5 printf("%ld %ld %ld",a[0][0][0],a[1][0][0],a[2][0][0]);
全球变暖 bfs,对原来的每一块赋予一个编号;之后记录每一个存在的块
原来的一个岛屿有可能被分成多个岛屿,这多个岛屿只能当一个算,大坑题
倍数问题 我比赛时候的方法是:
对于所有余数为k的数,记录前三大的数,
对于三个数,若前两个数的余数确定,则第三个数的余数可求出来
三种情况:三个数的余数相同;两个数的余数相同;三个数的余数都不同
for i = 0 to mod-1
for j = 0 to mod-1
k = 2*mod - i - j;
if i=j=k ,找到三个最大的余数为i的数(也许不存在)
……
时间复杂度:mod*mod(1 <= mod <= 10^3)
另一种方法:dp[i][j]为j个数之和模mod余数为i的 j个数最大值
时间复杂度:n * mod * 3(j=1,2,3) 1 <= n <= 10^5, 1 <= mod <= 10^3
超时一点点
付账问题 一个比较好想的贪心,标准差最小,当然是各个数都比较接近,
对n个值排序,从最小的数开始到最大的数,若这个值 小于 剩余需要支付的平均值,则对应的人支付所有的钱,即取该值,
直到这个值 大于等于 剩余需要支付的平均值x,对应的人及以后的人只有支付x即可
C/C++ B组:
递增三元组 排序+树状数组/二分 / 数据范围太小,直接数组记录值就可以
螺旋折线 找规律,得到四部分的式子,开long long
日志统计 排序+单调队列
乘积最大 按照绝对值排序,选最大的前k个数相乘,
若符号为负:
1.若前k个数有负数,从第k+1个开始,找到第一个正数,与前k个数中绝对值最小的负数进行交换;有可能找不到
2.若前k个数有正数,从第k+1个开始,找到第一个负数,与前k个数中绝对值最小的正数进行交换;有可能找不到
求1与2的结果的最大值
若符号为正或零:
就是当前结果
Java A组:
居然找不到题目……
Java B组:
堆的计数
1.完全二叉树(最底层从左向右放置)
2.父节点的权值一定小于其子节点的权值
3.根节点的值是确定的,值最小
4.任意n个值不相等的数,经过离散化值为1~n,不影响大小关系,
f(n)[以n个点组成的数]的值固定
f(n)=f(m)[左边的数目]*f(n-m-1)*C(n-1,m) [除根节点之外,选择任意m个数作为左边的点]
n!=2 p=log(n)/log(2) 层数
if n-2^p<2^(p-1) m = n-2^p+1 + 2^(p-1)-1 = n-2^(p-1)
else m = 2^(p-1) + 2^(p-1)-1 = 2^p-1
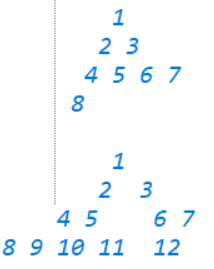
1.记忆化搜索:从n点开始,找m,n-m-1,然后接下来找…… vis记录之间已经计算过的状态
(记录一下需要算多少值)
2.c(x,y)中x,y的值的变化:
(4,2)、(5,3)、(6,3)、(7,3)、(8,4)、(9,5)、(10,6)、(11,7)、(12,7)、(13,7)、(14,7)、(15,7)……
两种情况:x++,y++ x++[n-2^p<2^(p-1)]
Way2:
37 #include <cstdio> 38 #include <cstdlib> 39 #include <cstring> 40 #include <cmath> 41 #include <list> 42 #include <stack> 43 #include <vector> 44 #include <set> 45 #include <map> 46 #include <queue> 47 #include <algorithm> 48 #include <iostream> 49 using namespace std; 50 #define mod 1000000009 51 long long f[100005]; 52 53 long long chu(long long s) 54 { 55 if (s==0) 56 return 1; 57 long ci=mod-1-1; 58 long long r=1; 59 while (ci) 60 { 61 if ((ci & 1)==1) 62 r=r*s%mod; 63 s=s*s%mod; 64 ci=ci>>1; 65 } 66 return r; 67 } 68 69 int main() 70 { 71 long n,m,p,i; 72 long long value=1; 73 scanf("%ld",&n); 74 f[0]=1; f[1]=1; 75 //f(n)=f(m)*f(n-m-1)*C(n-1,m) 76 m=0; 77 for (i=2;i<=n;i++) 78 { 79 p=(long)(log(i)/log(2)); 80 if (i - (1<<p) < (1<<(p-1)) ) 81 { 82 m++; 83 //C(i-1,m) <- C(i-2,m-1) 84 value=value * (i-1) %mod * chu(m) %mod; 85 f[i]=f[m] * f[i-m-1] %mod *value %mod; 86 } 87 else 88 { 89 //C(i-1,m) <- C(i-2,m) 90 value=value * (i-1) %mod * chu(i-m-1) %mod; 91 f[i]=f[m] * f[i-m-1] %mod * value %mod; 92 } 93 } 94 printf("%ld",f[n]); 95 return 0; 96 } 97 // 1 1 2 3 8 20 80
Way1:
1 /* 2 1.ÍêÈ«¶þ²æÊ÷(×îµ×²ã´Ó×óÏòÓÒ·ÅÖÃ) 3 4 2.¸¸½ÚµãµÄȨֵһ¶¨Ð¡ÓÚÆä×Ó½ÚµãµÄȨֵ 5 6 3.¸ù½ÚµãµÄÖµÊÇÈ·¶¨µÄ£¬Öµ×îС 7 8 4.ÈÎÒân¸öÖµ²»ÏàµÈµÄÊý£¬¾¹ýÀëÉ¢»¯ÖµÎª1~n£¬²»Ó°Ïì´óС¹Øϵ£¬ 9 f(n)[ÒÔn¸öµã×é³ÉµÄÊý]µÄÖµ¹Ì¶¨ 10 11 f(n)=f(m)[×ó±ßµÄÊýÄ¿]*f(n-m-1)*C(n-1,m) [³ý¸ù½ÚµãÖ®Í⣬ѡÔñÈÎÒâm¸öÊý×÷Ϊ×ó±ßµÄµã] 12 13 n!=2 p=log(n)/log(2) ²ãÊý 14 if n-2^p<2^(p-1) m = n-2^p+1 + 2^(p-1)-1 = n-2^(p-1) 15 else m = 2^(p-1) + 2^(p-1)-1 = 2^p-1 16 17 1 18 2 3 19 4 5 6 7 20 8 21 22 1 23 2 3 24 4 5 6 7 25 8 9 10 11 12 26 27 28 1.¼ÇÒ仯ËÑË÷£º´Ónµã¿ªÊ¼£¬ÕÒm,n-m-1£¬È»ºó½ÓÏÂÀ´ÕÒ¡¡ vis¼Ç¼֮¼äÒѾ¼ÆËã¹ýµÄ״̬ 29 (¼Ç¼һÏÂÐèÒªËã¶àÉÙÖµ) 30 31 2.c(x,y)ÖÐx,yµÄÖµµÄ±ä»¯: 32 (4,2)¡¢(5,3)¡¢(6,3)¡¢(7,3)¡¢(8,4)¡¢(9,5)¡¢(10,6)¡¢(11,7)¡¢(12,7)¡¢(13,7)¡¢(14,7)¡¢(15,7)¡¡ 33 Á½ÖÖÇé¿ö:x++,y++ x++[n-2^p<2^(p-1)] 34 35 */ 36 37 #include <cstdio> 38 #include <cstdlib> 39 #include <cstring> 40 #include <cmath> 41 #include <list> 42 #include <stack> 43 #include <vector> 44 #include <set> 45 #include <map> 46 #include <queue> 47 #include <algorithm> 48 #include <iostream> 49 using namespace std; 50 #define mod 1000000009 51 long long f[100005]; 52 53 long long chu(long long s) 54 { 55 if (s==0) 56 return 1; 57 long ci=mod-1-1; 58 long long r=1; 59 while (ci) 60 { 61 if ((ci & 1)==1) 62 r=r*s%mod; 63 s=s*s%mod; 64 ci=ci>>1; 65 } 66 return r; 67 } 68 69 long dfs(long d) 70 { 71 long m,p,i; 72 p=(long)(log(d)/log(2)); //d!=1,0 73 if (d - (1<<p) < (1<<(p-1)) ) 74 m = d - (1<<(p-1)); 75 else 76 m = (1<<p) - 1; 77 if (f[m]==-1) 78 dfs(m); 79 if (f[d-m-1]==-1) 80 dfs(d-m-1); 81 f[d]=f[m] * f[d-m-1] %mod; 82 for (i=d-1;i>d-1-m;i--) 83 f[d]=f[d]*i %mod; 84 for (i=2;i<=m;i++) 85 f[d]=f[d]*chu(i) %mod; 86 } 87 88 int main() 89 { 90 long n,i; 91 scanf("%ld",&n); 92 f[0]=1; f[1]=1; 93 for (i=2;i<=n;i++) 94 f[i]=-1; 95 //f(n)=f(m)*f(n-m-1)*C(n-1,m) 96 dfs(n); 97 printf("%ld",f[n]); 98 return 0; 99 } 100 // 1 1 2 3 8 20 80



