数分解问题:把一个数分解成很多数
数分解问题:把一个数分解成很多数
1.数字相同但位置不同的方案看作两个方法:
如5=1+1+2+3=2+3+1+1看作是不同的两个方法
f(n)= f(n-1)+f(n-2)+…+ f(1) +1 (第一个数字为1,2,…,n-1,n)
证明 f(n)=2^(n-1):
当n=1,f(1)=1=2^(1-1),
假设n<=k时,f(n)=2^(n-1),
则f(k+1)=1+1+2+…+2^(k-1)=2^k,得证。
Code:
1 #include <stdio.h> 2 #include <stdlib.h> 3 #define maxn 1000 4 5 long arr[maxn+1],pos=0,num=0; 6 7 void dfs(long d) 8 { 9 long i; 10 for (i=1;i<d;i++) 11 { 12 pos++; 13 arr[pos]=i; 14 dfs(d-i); 15 pos--; 16 } 17 num++; 18 printf("%ld : ",num); 19 //last element is d 20 for (i=1;i<=pos;i++) 21 printf("%ld ",arr[i]); 22 printf("%ld\n",d); 23 } 24 25 int main() 26 { 27 long n; 28 scanf("%ld",&n); 29 dfs(n); 30 printf("ans = %ld\n",num); 31 return 0; 32 }
Result:
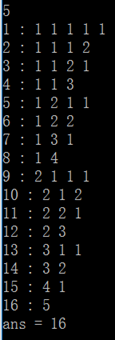
2. 数字相同但位置不同的方案看作一个方法
如5=1+1+2+3=2+3+1+1看作是同一个方法
程序做法:按从小到大(可以相同)排序,这样就保证不重复
如4=1+1+1+1 (1<=1<=1<=1) =1+1+2 (1<=1<=2) =1+3 (1<3) =4
t(n,k):对数字n分解,最大的数为k的方法数
I.(n<>k)
t(n,k)=t(n-k,1)+t(n-k,2)+t(n-k,3)+……+t(n-k,s)
(s满足s<=k且s<= n-k)
II.(n=k)
t(n,k)=1
f(n)=t(n,n)+t(n,n-1)+t(n,n-2)+t(n,1)
Code:
1 #include <stdio.h> 2 #include <stdlib.h> 3 #define maxn 1000 4 5 long arr[maxn+1],pos=0,num=0; 6 7 void dfs(long d) 8 { 9 long i; 10 //arr[pos+1](i)>=arr[pos] 11 //所以要初始化arr[0]=1 12 for (i=arr[pos];i<d;i++) 13 { 14 pos++; 15 arr[pos]=i; 16 dfs(d-i); 17 pos--; 18 } 19 if (d>=arr[pos]) 20 { 21 num++; 22 printf("%ld : ",num); 23 //last element is d 24 for (i=1;i<=pos;i++) 25 printf("%ld ",arr[i]); 26 printf("%ld\n",d); 27 } 28 } 29 30 int main() 31 { 32 long n; 33 scanf("%ld",&n); 34 arr[0]=1; 35 dfs(n); 36 printf("ans = %ld\n",num); 37 return 0; 38 }
Result:

求方法总数:
Code:
1 #include <stdio.h> 2 #include <stdlib.h> 3 #define maxn 1000 4 5 long t[maxn+1][maxn+1],f[maxn]; 6 7 long min(long a,long b) 8 { 9 if (a>b) 10 return b; 11 else 12 return a; 13 } 14 15 int main() 16 { 17 long n,i,j,k; 18 scanf("%ld",&n); 19 for (i=1;i<=n;i++) 20 { 21 t[i][i]=1; 22 for (j=1;j<=i-1;j++) 23 t[i][j]=0; 24 f[i]=0; 25 } 26 //t(n,k)=t(n-k,1)+t(n-k,2)+t(n-k,3)+……+t(n-k,s) 27 for (i=2;i<=n;i++) 28 for (k=1;k<i;k++) 29 //t(i,k) 30 for (j=1;j<=min(k,i-k);j++) 31 t[i][k]+=t[i-k][j]; 32 for (i=1;i<=n;i++) 33 for (j=i;j>=1;j--) 34 f[i]+=t[i][j]; 35 for (i=1;i<=n;i++) 36 printf("%ld : %ld\n",i,f[i]); 37 return 0; 38 }
Situation:
n =1,2,3,4,5,6 , 7 , 8 , 9 , 10
Total =1,2,3,5,7,11,15,22,30,42
3.数字不允许重复
如不可以5=3+1+1 (不能有两个1)
程序做法:按从小到大(不可以相同)排序,这样就保证不重复
如6=1+2+3 (1<2<3) =1+5 (1<5) =2+4 (2<4) =6
t(n,k):对数字n分解,最大的数为k的方法数
I.(n<>k)
t(n,k)=t(n-k,1)+t(n-k,2)+t(n-k,3)+……+t(n-k,s)
(s满足s<k且s<= n-k)
II.(n=k)
t(n,k)=1
f(n)=t(n,n)+t(n,n-1)+t(n,n-2)+t(n,1)
Code:
1 #include <stdio.h> 2 #include <stdlib.h> 3 #define maxn 1000 4 5 long arr[maxn+1],pos=0,num=0; 6 7 void dfs(long d) 8 { 9 long i; 10 //arr[pos+1](i)>arr[pos] 11 //所以要初始化arr[0]=0 12 //与程序2(i=arr[pos])不同 13 for (i=arr[pos]+1;i<d;i++) 14 { 15 pos++; 16 arr[pos]=i; 17 dfs(d-i); 18 pos--; 19 } 20 //与程序2(d>=arr[pos])不同 21 if (d>arr[pos]) 22 { 23 num++; 24 printf("%ld : ",num); 25 //last element is d 26 for (i=1;i<=pos;i++) 27 printf("%ld ",arr[i]); 28 printf("%ld\n",d); 29 } 30 } 31 32 int main() 33 { 34 long n; 35 scanf("%ld",&n); 36 arr[0]=0; 37 dfs(n); 38 printf("ans = %ld\n",num); 39 return 0; 40 }
Result:

求方法总数:
Code:
1 #include <stdio.h> 2 #include <stdlib.h> 3 #define maxn 1000 4 5 long t[maxn+1][maxn+1],f[maxn]; 6 7 long min(long a,long b) 8 { 9 if (a>b) 10 return b; 11 else 12 return a; 13 } 14 15 int main() 16 { 17 long n,i,j,k; 18 scanf("%ld",&n); 19 for (i=1;i<=n;i++) 20 { 21 t[i][i]=1; 22 for (j=1;j<=i-1;j++) 23 t[i][j]=0; 24 f[i]=0; 25 } 26 //t(n,k)=t(n-k,1)+t(n-k,2)+t(n-k,3)+……+t(n-k,s) 27 for (i=2;i<=n;i++) 28 for (k=1;k<i;k++) 29 //t(i,k) 30 //与程序2(j<=min(k,i-k))不同的地方 31 for (j=1;j<=min(k-1,i-k);j++) 32 t[i][k]+=t[i-k][j]; 33 for (i=1;i<=n;i++) 34 for (j=i;j>=1;j--) 35 f[i]+=t[i][j]; 36 for (i=1;i<=n;i++) 37 printf("%ld : %ld\n",i,f[i]); 38 return 0; 39 }
Situation:
n =1,2,3,4,5,6,7,8,9,10
Total =1,1,2,2,3,4,5,6,8,10



