[Offer收割]编程练习赛13 解题报告
http://hihocoder.com/contest/offers13/problems
题目1 : 风格不统一如何写程序
首先:输入保证组成变量名的单词只包含小写字母。
做法:只要对不同的部分进行修改即可
注意:只有一个单词,两个方法的单词都一样
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <string.h> 4 #include <stdbool.h> 5 6 int main() 7 { 8 long n,i,k,len; 9 char s[101]; 10 bool vis; 11 scanf("%ld",&n); 12 for (k=1;k<=n;k++) 13 { 14 scanf("%s",s); 15 len=strlen(s); 16 vis=false; 17 for (i=0;i<len;i++) 18 if (s[i]=='_') 19 { 20 vis=true; 21 break; 22 } 23 if (vis) 24 { 25 for (i=0;i<len;i++) 26 if (s[i]=='_') 27 { 28 printf("%c",s[i+1]-32); 29 i++; 30 } 31 else 32 printf("%c",s[i]); 33 } 34 else 35 { 36 for (i=0;i<len;i++) 37 if (s[i]<97) 38 { 39 printf("_"); 40 printf("%c",s[i]+32); 41 } 42 else 43 printf("%c",s[i]); 44 } 45 printf("\n"); 46 } 47 48 return 0; 49 }
最大子矩阵
注意:满足条件最大的子矩阵所包含的元素数目。如果没有子矩阵满足条件,输出-1。
与求最大子矩阵题目(hdu1559子矩阵的元素之和最大)方法类似。
设row[x][y]:第x行中前y个数的和
则row[x][q]-row[x][p]:第x行中第p+1~第q个数的和
行x~y列u~v的矩形的元素之和:row[x][v]-row[x][u-1]+row[x+1][v]-row[x+1][u-1]+…+row[y][v]-row[y][u-1]
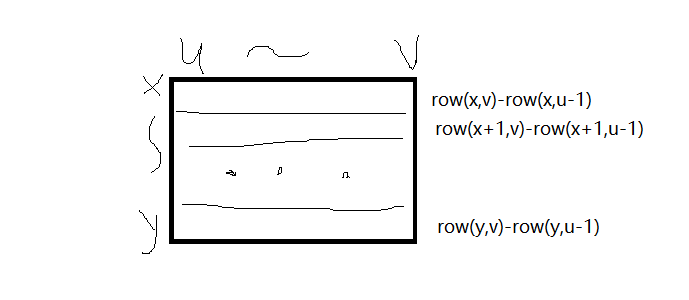
按照列固定:u~v (第u个数到第v个数), 进行行的探索。
假设从行第p个数开始向下边2递增(每次p加1),假设到第q个数数值和第一次超过设定值,计算矩形面积(q-p)*(v-u+1),
然后从第p个数开始向下边1递增(每次p+1),直到数值和第一次小于设定值。
然后继续操作,直到v=n+1,结束。

而对于每个列固定:x~y,共m*m次。而对于每次行的探索,每个数最多加入一次,每个数最多减去一次,共2*n次。
时间复杂度O(m*m*n)。当然如果m>n,可以把行固定,进行列的探索,时间复杂度O(m*n*n)。
即时间复杂度O(m*n*min(m,n))。
参见程序,比较巧妙。
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 long max(long a,long b) 5 { 6 if (a>b) 7 return a; 8 else 9 return b; 10 } 11 12 int main() 13 { 14 long n,m,f[260][260],row[260][260]; 15 long i,j,s,t,maxg=0,maxvalue,ans=0,bian,x,y; 16 scanf("%ld%ld%ld",&n,&m,&maxvalue); 17 for (i=1;i<=n;i++) 18 { 19 //single row 20 row[i][0]=0; 21 for (j=1;j<=m;j++) 22 { 23 scanf("%ld",&f[i][j]); 24 row[i][j]=row[i][j-1]+f[i][j]; 25 } 26 } 27 //s+1~t 28 for (s=0;s<m;s++) 29 for (t=s+1;t<=m;t++) 30 { 31 bian=t-s; 32 ans=0; 33 x=1; 34 y=1; 35 i=1; 36 while (i!=n+1) 37 { 38 for (i=y;i<=n;i++) 39 { 40 ans=ans+row[i][t]-row[i][s]; 41 if (ans>maxvalue) 42 break; 43 } 44 //x~i-1 45 maxg=max(maxg,(i-x)*bian); 46 //使x~i <=maxvalue 47 //最终的可能性是减为0 48 while (ans>=maxvalue) 49 { 50 ans=ans-row[x][t]+row[x][s]; 51 x++; 52 } 53 //使下一次从i+1的位置开始加 54 y=i+1; 55 56 } 57 } 58 if (maxg==0) 59 printf("-1\n"); 60 else 61 printf("%ld\n",maxg); 62 return 0; 63 } 64 /* 65 5 5 3 66 1 2 3 2 1 67 2 3 1 2 3 68 1 2 1 3 1 69 1 2 1 3 1 70 1 2 3 3 3 71 */ 72 /* 73 20 20 31 74 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 75 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 76 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 77 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 78 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 79 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 80 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 81 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 82 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 83 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 84 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 85 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 86 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 87 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 88 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 89 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 90 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 91 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 92 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 93 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 94 */
题目3 : 一人麻将
注意:无法胡牌输出-1。
方法:可以cheat!!!经测试,输出-1,可得10分。那时我去参加zoj的网赛,没有时间了,就果断cheat!(noip及其有效,对一些特殊且容易写的部分)
参见程序,程序长,但时间消耗比较短
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <stdbool.h> 4 5 struct rec 6 { 7 long posu,posv; 8 }; 9 10 struct node 11 { 12 long posu,posv,posw; 13 }; 14 15 bool vis[108]; 16 struct node s[1800]; 17 long ts,ee,minpos=200; 18 19 int cmp(const void *a,const void *b) 20 { 21 //posu<posv。对a,b中最大的牌(posv)进行升序排序(先拿到,先胡牌) 22 //a,b中最大的牌(posv)都不相同 23 return (*(struct rec *)a).posv - (*(struct rec *)b).posv; 24 } 25 26 int cmp1(const void *a,const void *b) 27 { 28 return (*(struct node *)a).posw - (*(struct node *)b).posw; 29 } 30 31 long max(long a,long b) 32 { 33 if (a>b) 34 return a; 35 else 36 return b; 37 } 38 39 long min(long a,long b) 40 { 41 if (a>b) 42 return b; 43 else 44 return a; 45 } 46 47 void dfs(long b,long step) 48 { 49 long i; 50 for (i=b;i<ts-step && s[i].posw<minpos;i++) 51 if (vis[s[i].posu] && vis[s[i].posv] && vis[s[i].posw]) 52 { 53 if (step==0) 54 { 55 //minpos=min(minpos,s[i].posw); 56 minpos=max(ee,s[i].posw); 57 break; 58 } 59 //else if (s[i].posw<minpos) 60 else 61 { 62 vis[s[i].posu]=false; 63 vis[s[i].posv]=false; 64 vis[s[i].posw]=false; 65 dfs(i+1,step-1); 66 vis[s[i].posu]=true; 67 vis[s[i].posv]=true; 68 vis[s[i].posw]=true; 69 } 70 } 71 } 72 73 int main() 74 { 75 char str[3]; 76 //一张牌最多4个:2对,9*2=18种牌 77 //3: 78 //数字相连:(1,2,3)~(7,8,9) 每张牌有4种选择 4*4*4*8=502 79 //同数字:若有四张牌 1,2,3;2,3,4(若1,2,3与其它冲突,用2,3,4) 2*9=18 80 struct rec er[3][30],e[90]; 81 struct node san[3][600]; 82 long ge[3],gs[3],te; 83 //pai[i][j]:i:对应a,b,c j:对应1~9,最多有4张牌 84 long n,x,y,t,pai[3][9][4],ans[3][9]; 85 long i,j,k,l,m; 86 for (i=0;i<3;i++) 87 for (j=0;j<9;j++) 88 ans[i][j]=0; 89 scanf("%ld",&n); 90 91 for (i=0;i<14;i++) 92 { 93 scanf("%s",str); 94 x=str[0]-97; 95 //-'1' 96 y=str[1]-49; 97 pai[x][y][ans[x][y]]=i; 98 ans[x][y]++; 99 } 100 for (i=14;i<14+n;i++) 101 { 102 scanf("%s",str); 103 x=str[0]-97; 104 y=str[1]-49; 105 pai[x][y][ans[x][y]]=i; 106 ans[x][y]++; 107 } 108 109 //对子 110 for (i=0;i<3;i++) 111 { 112 ge[i]=0; 113 for (j=0;j<9;j++) 114 { 115 //找最前面的配对 116 if (ans[i][j]>=2) 117 { 118 er[i][ge[i]].posu=pai[i][j][0]; 119 er[i][ge[i]].posv=pai[i][j][1]; 120 ge[i]++; 121 } 122 //两个对子 123 if (ans[i][j]==4) 124 { 125 er[i][ge[i]].posu=pai[i][j][2]; 126 er[i][ge[i]].posv=pai[i][j][3]; 127 ge[i]++; 128 } 129 } 130 qsort(er[i],ge[i],sizeof(struct rec),cmp); 131 } 132 133 //至少拥有7个对子胡牌 134 //手中14张牌最多只能属于两个花色 135 //each 对子 没有相互影响 136 for (i=0;i<2;i++) 137 for (j=i+1;j<3;j++) 138 if (ge[i]+ge[j]>=7) 139 { 140 x=0; 141 y=0; 142 t=0; 143 while (x<ge[i] && y<ge[j] && t<6) 144 { 145 t++; 146 if (er[i][x].posv<er[j][y].posv) 147 x++; 148 else 149 y++; 150 } 151 if (t==6) 152 { 153 //use j 154 if (x==ge[i]) 155 minpos=min(minpos,er[j][y].posv); 156 //use i 157 else if (y==ge[j]) 158 minpos=min(minpos,er[i][x].posv); 159 else 160 minpos=min(minpos,min(er[i][x].posv,er[j][y].posv)); 161 } 162 //use j 163 else if (x==ge[i]) 164 minpos=min(minpos,er[j][y+6-t].posv); 165 //use i 166 else 167 minpos=min(minpos,er[i][x+6-t].posv); 168 } 169 170 //三张牌 171 for (i=0;i<3;i++) 172 { 173 gs[i]=0; 174 //同数字 175 for (j=0;j<9;j++) 176 { 177 if (ans[i][j]>=3) 178 { 179 san[i][gs[i]].posu=pai[i][j][0]; 180 san[i][gs[i]].posv=pai[i][j][1]; 181 san[i][gs[i]].posw=pai[i][j][2]; 182 gs[i]++; 183 } 184 if (ans[i][j]==4) 185 { 186 //相同的牌先给别人用了 187 san[i][gs[i]].posu=pai[i][j][1]; 188 san[i][gs[i]].posv=pai[i][j][2]; 189 san[i][gs[i]].posw=pai[i][j][3]; 190 gs[i]++; 191 } 192 } 193 //数字相连 194 for (j=0;j<7;j++) 195 for (k=0;k<ans[i][j];k++) 196 for (l=0;l<ans[i][j+1];l++) 197 for (m=0;m<ans[i][j+2];m++) 198 { 199 san[i][gs[i]].posu=pai[i][j][k]; 200 san[i][gs[i]].posv=pai[i][j+1][l]; 201 san[i][gs[i]].posw=pai[i][j+2][m]; 202 //posw存放最大值 203 if (san[i][gs[i]].posu>san[i][gs[i]].posw) 204 { 205 if (san[i][gs[i]].posu>san[i][gs[i]].posv) 206 { 207 t=san[i][gs[i]].posu; 208 san[i][gs[i]].posu=san[i][gs[i]].posw; 209 san[i][gs[i]].posw=t; 210 } 211 else 212 { 213 t=san[i][gs[i]].posv; 214 san[i][gs[i]].posv=san[i][gs[i]].posw; 215 san[i][gs[i]].posw=t; 216 } 217 } 218 else if (san[i][gs[i]].posv>san[i][gs[i]].posw) 219 { 220 t=san[i][gs[i]].posv; 221 san[i][gs[i]].posv=san[i][gs[i]].posw; 222 san[i][gs[i]].posw=t; 223 } 224 gs[i]++; 225 } 226 qsort(san[i],gs[i],sizeof(struct node),cmp1); 227 } 228 229 //4*3+2 230 for (i=0;i<2;i++) 231 for (j=i+1;j<3;j++) 232 { 233 for (k=0;k<108;k++) 234 vis[k]=true; 235 236 te=0; 237 for (k=0;k<ge[i];k++) 238 if (er[i][k].posv<minpos) 239 { 240 e[te]=er[i][k]; 241 te++; 242 } 243 else 244 break; 245 for (k=0;k<ge[j];k++) 246 if (er[j][k].posv<minpos) 247 { 248 e[te]=er[j][k]; 249 te++; 250 } 251 else 252 break; 253 254 ts=0; 255 for (k=0;k<gs[i];k++) 256 if (san[i][k].posw<minpos) 257 { 258 s[ts]=san[i][k]; 259 ts++; 260 } 261 else 262 break; 263 for (k=0;k<gs[j];k++) 264 if (san[j][k].posw<minpos) 265 { 266 s[ts]=san[j][k]; 267 ts++; 268 } 269 270 qsort(e,te,sizeof(struct rec),cmp); 271 qsort(s,ts,sizeof(struct node),cmp1); 272 273 for (k=0;k<te;k++) 274 { 275 if (e[k].posv<minpos) 276 { 277 ee=e[k].posv; 278 vis[e[k].posu]=false; 279 vis[e[k].posv]=false; 280 dfs(0,3); 281 vis[e[k].posu]=true; 282 vis[e[k].posv]=true; 283 } 284 else 285 break; 286 } 287 } 288 //No Solution: output -1 289 if (minpos==200) 290 printf("-1\n"); 291 else 292 printf("%ld\n",minpos-13); 293 return 0; 294 }
题目拓展:
有n个人,参加一个活动
每一个人有一个不和谐值
每三个人一个队伍
有若干组队伍
每一个队伍的不和谐值为三人的不和谐值的最大值
而不和谐值越小,完成一个活动越快
要求从n个人从选出m个队伍,
其中不同队伍里不能有相同的人
使不和谐值最大的队伍的不和谐值最小,
从而使得所有队伍完成时间最短
当三个人
变为两个人
变为k个人
结果如何???
题目4 : 骑士游历
一个通俗的想法:f[k][i][j],第k步可以到达(i,j)的步法总数。
f[k+1][i][j]是在第k步的基础上走1步到达(i,j)的步法总数。
1 #include <stdio.h> 2 #include <stdlib.h> 3 #define yu 1000000007 4 5 int main() 6 { 7 long dx[8]={-2,-2,-1,-1,1,1,2,2}; 8 long dy[8]={-1,1,-2,2,-2,2,-1,1}; 9 long long f[2][12][12]; 10 long n,r,c,i,j,k,step,pre,cur,x,y; 11 long long ans; 12 scanf("%ld%ld%ld",&n,&r,&c); 13 for (i=1;i<=8;i++) 14 for (j=1;j<=8;j++) 15 f[0][i][j]=0; 16 f[0][r][c]=1; 17 pre=0; 18 cur=1; 19 for (step=1;step<=n;step++) 20 { 21 for (i=1;i<=8;i++) 22 for (j=1;j<=8;j++) 23 f[cur][i][j]=0; 24 for (i=1;i<=8;i++) 25 for (j=1;j<=8;j++) 26 for (k=0;k<8;k++) 27 { 28 x=i+dx[k]; 29 y=j+dy[k]; 30 if (x>=1 && x<=8 && y>=1 && y<=8) 31 f[cur][x][y]=(f[cur][x][y]+f[pre][i][j])%yu; 32 } 33 34 pre=pre ^ 1; 35 cur=cur ^ 1; 36 } 37 ans=0; 38 for (i=1;i<=8;i++) 39 for (j=1;j<=8;j++) 40 ans=(ans+f[pre][i][j])%yu; 41 printf("%lld\n",ans); 42 return 0; 43 }
满分做法:
二分思想,类似快速幂思想
f[k][x][y][u][v]:从(x,y)开始走k步到(u,v)总的走法
1.第k步到达第k+1步
f[k+1][x][y][u][v]=sum(f[k][x][y][p][q]+f[1][p][q][u][v])
2.第k步到达第2*k步
f[2*k][x][y][u][v]=sum(f[k][x][y][p][q],f[k][p][q][u][v])
快速幂:1->k,如10101=(((1*2+0)*2+1)*2+0)*2+1。(乘4次,加5次)
初始化f[1],只要创建四维数组即可。
时间复杂度:
1.第k步到达第2*k步:x,y,p,q,u,v可以取1~8:8*8*8*8*8*8=262144
最多执行log2(1000000000)<=30(向下取整)
262144*30=7864320
2.第k步到达第k+1步:f[k+1][x][y][u][v]=sum(f[k][x][y][p][q]+f[1][p][q][u][v]):计算每个x,y:8*8*8(走马,8种操作)=512
最多执行log2(1000000000)<=30(向下取整)
时间复杂度可以忽略不计
总的时间复杂度小于1000万,不会超时。
参见程序
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <math.h> 4 #define yu 1000000007 5 6 int main() 7 { 8 long dx[8]={-2,-2,-1,-1,1,1,2,2}; 9 long dy[8]={-1,1,-2,2,-2,2,-1,1}; 10 long long f[9][9][9][9],t[9][9][9][9],ans; 11 long n,r,c,m,ch[32]; 12 long x,y,p,q,u,v,k,i; 13 14 scanf("%ld%ld%ld",&n,&r,&c); 15 for (x=1;x<=8;x++) 16 for (y=1;y<=8;y++) 17 for (u=1;u<=8;u++) 18 for (v=1;v<=8;v++) 19 f[x][y][u][v]=0; 20 for (u=1;u<=8;u++) 21 for (v=1;v<=8;v++) 22 for (k=0;k<8;k++) 23 { 24 p=u-dx[k]; 25 q=v-dy[k]; 26 if (p>=1 && p<=8 && q>=1 && q<=8) 27 f[p][q][u][v]=1; 28 } 29 30 m=(long)(log(n)/log(2.0)); 31 ch[0]=1; 32 for (i=1;i<=m;i++) 33 ch[i]=ch[i-1]<<1; 34 n-=ch[m]; 35 for (i=m-1;i>=0;i--) 36 { 37 //*2 38 for (x=1;x<=8;x++) 39 for (y=1;y<=8;y++) 40 for (u=1;u<=8;u++) 41 for (v=1;v<=8;v++) 42 { 43 t[x][y][u][v]=f[x][y][u][v]; 44 f[x][y][u][v]=0; 45 } 46 47 for (x=1;x<=8;x++) 48 for (y=1;y<=8;y++) 49 for (u=1;u<=8;u++) 50 for (v=1;v<=8;v++) 51 { 52 f[x][y][u][v]=0; 53 for (p=1;p<=8;p++) 54 for (q=1;q<=8;q++) 55 f[x][y][u][v]=(f[x][y][u][v]+t[x][y][p][q]*t[p][q][u][v])%yu; 56 } 57 //+1 58 if (n>=ch[i]) 59 { 60 for (x=1;x<=8;x++) 61 for (y=1;y<=8;y++) 62 for (u=1;u<=8;u++) 63 for (v=1;v<=8;v++) 64 { 65 t[x][y][u][v]=f[x][y][u][v]; 66 f[x][y][u][v]=0; 67 } 68 69 for (u=1;u<=8;u++) 70 for (v=1;v<=8;v++) 71 for (k=0;k<8;k++) 72 { 73 p=u-dx[k]; 74 q=v-dy[k]; 75 if (p>=1 && p<=8 && q>=1 && q<=8) 76 { 77 for (x=1;x<=8;x++) 78 for (y=1;y<=8;y++) 79 f[x][y][u][v]=(f[x][y][u][v]+t[x][y][p][q])%yu; 80 } 81 } 82 n-=ch[i]; 83 } 84 } 85 ans=0; 86 for (u=1;u<=8;u++) 87 for (v=1;v<=8;v++) 88 ans=(ans+f[r][c][u][v])%yu; 89 printf("%lld",ans); 90 return 0; 91 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号