abc359(atcoder beginer 359) C、D、E、F

 

C

这类小模拟题

1. 结果处理分类。可以用swap、函数等方法，简化类别

2. 不同的写法有可能是对称的

3. 这次用vscode，感觉chatgpt的自动补全很好，的确能理解我前面代码的意思，补全我当前代码可能的内容

4. 多造样例，有规律的

atcoder beginer基本上都有这样一道题

 

D

我比赛上的方法：

 

 dp+细节题

f[i][j] = sum{f[i-1][l]}

i：第i位

j：该位及前面k位

f[i][j]：可用数目

l：所有满足的情况

不用记录当前这位的情况

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define ULL unsigned long long

const LL mod_2=998244353;

const double eps_1=1e-5;
const double eps_2=1e-10;

const int maxn=1e3+10;
const int maxe=1024+10;
const int maxlen=12;

int len,er[maxlen],q[maxlen];
int pos[maxe][maxlen],pal[maxe];
LL f[maxn][maxe],result=0;
string str;

void cal_value(int x)
{
    int i,j,cnt_q=0,value=0,value_new,last_value,last_ch,pre_ch;
    for (i=x-len+1;i<=x;i++)
    {
        if (str[i]=='B')
            value += er[i - (x-len+1)];
        else if (str[i]=='?')
            q[cnt_q++] = i - (x-len+1);
    }

    for (i=0;i<er[cnt_q];i++)
    {
        value_new = value;
        for (j=0;j<cnt_q;j++)
            value_new += er[ q[j] ] * pos[i][j];
        if (!pal[value_new])
        {
            if (str[x]!='?')
                last_ch = str[x]-'A';
            else
                last_ch = pos[i][cnt_q-1];
            
            if (x==len-1)
                f[x][value_new] = (f[x][value_new] + 1) % mod_2;
            else
            {
                if (str[x-len]!='?')
                {
                    pre_ch = str[x-len]-'A';
                    last_value = (value_new - last_ch * er[len-1]) * 2 + pre_ch;
                    if (!pal[last_value])
                        f[x][value_new] =(f[x][value_new] + f[x-1][last_value]) % mod_2;
                }
                else
                {
                    for (pre_ch=0;pre_ch<2;pre_ch++)
                    {
                        last_value = (value_new - last_ch * er[len-1]) * 2 + pre_ch;
                        if (!pal[last_value])
                            f[x][value_new] =(f[x][value_new] + f[x-1][last_value]) % mod_2;
                    }
                }
            }
        }
    }

}

int main()
{
    int n,i,j,v;
    cin>>n>>len>>str;

    for (i=0;i<=len;i++)
        er[i] = 1<<i;
    memset(pal,0,sizeof(pal));
    for (i=0;i<er[len];i++)
    {
        v = i;
        for (j=0;j<len;j++)
        {
            pos[i][j] = v & 1;
            v>>=1;
        }

        for (j=0;j<len/2;j++)
            if (pos[i][j]!=pos[i][len-j-1])
                break;
        if (j==len/2)
            pal[i] = 1;
    }

    memset(f,0,sizeof(f));
    for (i=len-1;i<n;i++)
        cal_value(i);

    for (i=0;i<er[len];i++)
        result = (result + f[n-1][i]) % mod_2;
    cout<<result;

    return 0;
}

 

我觉得这个代码写得比较长，找一下别人的代码，看怎么写这个000、001、010、011、100、…… 比较方便快捷 

 

chatgpt也是这样写

 

遍历从0到2^k，看当前串（当前这位是最靠右的位置）是否满足条件，这样感觉好写一点

感觉好写不少

j是前k位

l是当前位

 

j=0 to 1<<k 这样的写法，真的很爽。这样就不用一一找出所有的可能。如果当前写法不满足条件，前面dp[j]的值已经判断过了，肯定为0

l=0t o 2 这样的写法，真的很爽。这样就不用判断所有的情况，只用 if xxx continue就行

 

当DP能经常抱着这样的念头写的时候，就到了一定境界，代码数会少很多

 

还有比如只判断一半，没必要，全部判断好写

        for (j=0;j<k;j++)
            if (((i>>j)&1) != ((i>>(k-j-1))&1))
                ok=0;

 

 Submission #54807940 - UNIQUE VISION Programming Contest 2024 Summer (AtCoder Beginner Contest 359)

 

自己复写一下：

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define ULL unsigned long long

const LL mod_2=998244353;

const double eps_1=1e-5;
const double eps_2=1e-10;

const int maxn=1e3+10;
const int maxe=1024+10;

LL dp[maxn][maxe],result=0;
bool pal[maxe];

int main()
{
    LL n,k,i,j,l,ok,new_i;
    string str;
    cin>>n>>k>>str;

    for (i=0;i<(1<<k);i++)
    {
        ok=1;
        for (j=0;j<k;j++)
            if (((i>>j)&1) != ((i>>(k-j-1))&1))
                ok=0;
        pal[i] = ok ^ 1;
    }

    memset(dp,0,sizeof(dp));
    for (i=0;i<(1<<k);i++)
    {
        ok=1;
        for (j=0;j<k;j++)
        {
            if (str[j]=='A' && ((i>>j)&1) == 1)
                ok=0;
            if (str[j]=='B' && ((i>>j)&1) == 0)
                ok=0;
        }
        dp[k-1][i]=ok * pal[i];

    }

    for (j=k;j<n;j++)
        for (l=0;l<2;l++)
        {
            if (str[j]=='A' && l==1)
                continue;

            if (str[j]=='B' && l==0)
                continue;

            for (i=0;i<(1<<k);i++)
            {
                new_i = i/2+(1<<(k-1))*l;
                if (pal[new_i])
                    (dp[j][new_i] += dp[j-1][i]) %= mod_2;
            }
                
        }

    for (i=0;i<(1<<k);i++)
        (result += dp[n-1][i]) %= mod_2;
    cout<<result;
    return 0;
}

 

看前面几个人的代码，很短，不想看了…… emmm，就，找看得舒服的看就好，有大把选择

 

看题解，python代码很短

 是否回文数：

 

那c++的string也能一行解决

 

 

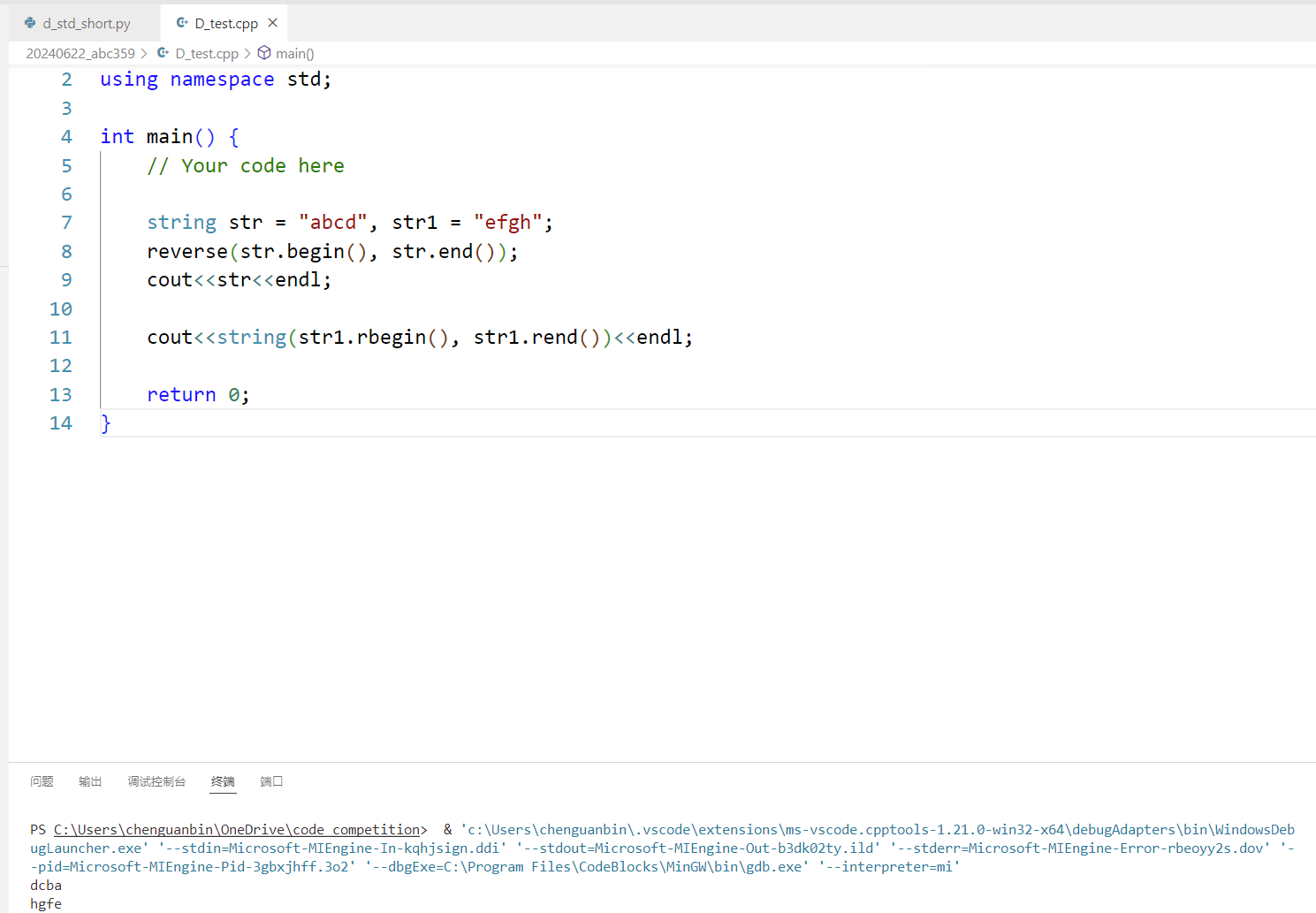
 不错不错

 

这个是当前向左所有长度为k的字符情况 -> 下一个字符向左所有长度为k的字符情况

这句话写得妙

 

tmp和mp就是起到，dp降维的作用而已

 

 这个是为了起到一开始不用预处理的作用。c++也可以在字符串前面添加，CC...C（k-1个C这样的操作），因为它无法构成回文数

 

字典序表的操作，学会了。这个代码的一些指令，多看多学多写，平时自己用python不熟，这个是很好的模板

N, K = map(int, input().split())

S = input()

# Initially, fill with characters that are not A nor B
mp = {'C' * (K - 1) : 1}

for c in S:
    # Add one character to the tail
    # Merge the cases for adding 'A' and adding 'B'
    # If both addition is impossible, merge an empty dictionary
    tmp = ({s + 'A' : v for s, v in mp.items()} if c != 'B' else {}) | ({s + 'B' : v for s, v in mp.items()} if c != 'A' else {})
    
    mp = {} # Erase the DP table
    
    for s, v in tmp.items():
        if s != s[::-1]: # If it is not a palindrome, drop the first character and add it
            if s[1:] in mp:
                mp[s[1:]] += v
            else:
                mp[s[1:]] = v

# The sum modulo 998244353 is the answer
print(sum(mp.values()) % 998244353)

 

 

 

 

E

题意很好懂，这类题，图文并茂。

当前位置i从右到左，找到第一个比它高的数（位置为j），结果（r[i]）等于r[j]+h[i]*(i-j)，如果没有，结果等于h[i]*(i+1)。结果要统一加个1。

 

栈

就觉得和栈有关系，但是太久没写了，所以emmm，没用这个方法

 

st算法

可以log(n)获得答案，跟2的倍数有关的。

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define ULL unsigned long long

const LL mod_1=1e9+7;
const LL mod_2=998244353;

const double eps_1=1e-5;
const double eps_2=1e-10;

const int maxn=2e5+10;

LL h[maxn],r[maxn];
LL maxh[maxn][20], ltr[maxn],er[20];

int main()
{
    LL n,i,j,k,l;
    for (i=0;i<20;i++)
        er[i] = 1<<i;

    cin>>n;
    for (i=0;i<n;i++)
    {
        cin>>h[i];
        if (i==0)
            ltr[i]=h[i];
        else
            ltr[i]=max(ltr[i-1],h[i]);
    }
        
    
    memset(maxh,0,sizeof(maxh));
    for (i=0;i<=20;i++)
    {
        k=1<<i;
        if (k>n)
            break;
        if (i==0)
        {
            for (j=0;j<n;j++)
                maxh[j][0]=h[j];
        }
        else
        {
            for (j=k;j<n;j++)
                maxh[j][i]=max(maxh[j][i-1],maxh[j-k/2][i-1]);
            for (j=0;j<k;j++)
                maxh[j][i]=ltr[j];
        }
    }

    for (i=0;i<n;i++)
    {
        if (i==0)
        {
            r[i]=h[i];
            continue;
        }
        
        if (ltr[i-1]<=h[i])
        {
            r[i]=h[i]*(i+1);
            continue;
        }
        

        j=1;
        k=0;
        while (j<=i)    //也可以<号，因为无法到达0的位置
        {
            j=j<<1;
            k++;
        }

        l=i-1;
        while (k--)
        {
            if (maxh[l][k]<h[i])
                l=l-er[k];
        }
        r[i]=r[l] + (i-l)*h[i];
    }

    for (i=0;i<n;i++)
    {
        cout<<r[i]+1;
        if (i==n-1)
            cout<<"\n";
        else
            cout<<" ";
    }


    return 0;
}

 

F

要习惯补beginner赛后的F题。否则，一直少做相对难，比赛上因为做得慢导致稍作的题，技术很难提升甚至倒退

700多个人对。很多了。前面排名的人，人均5分钟切F题

 

 

 

熟悉数据结构中树的特性，很重要。

只要满足：

1. di>=1

2. sum(di)=2N-2

无论树怎么构造都行

 

DP O(N*N) 复杂度超了

可以设置当 di*xi*xi的时候，当xi加1，数值加上di*(2*xi+1)，这个数值是递增的

那么一开始所有xi都等于1，然后提供N-2次给xi(i=1~n都可以)加1的机会

每次修改加1数值最小的，用优先队列记录，复杂度O(NlogN)

代码很短，可以写得很快。atcoder特色？

 

另外看到有人用

 typedef array<LL,3> par; 2 priority_queue<par, vector<par>, greater<par> > que;  

另外，也可以需要的变量减为两个(x的增量，x)，下次变为(x的增量+2*x，x)

 

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define ULL unsigned long long

const LL mod_1=1e9+7;
const LL mod_2=998244353;

const double eps_1=1e-5;
const double eps_2=1e-10;

const int maxn=2e5+10;

LL a[maxn];
typedef pair<LL, pair<LL, LL> > par;
priority_queue<par,vector<par>,greater<par> > que;
par p;

int main()
{
    LL n,i,result=0;
    cin>>n;
    for (i=0;i<n;i++)
    {
        cin>>a[i];
        que.push( make_pair(a[i]*(2*2-1*1), make_pair(a[i],1) ) );
        result += a[i];
    }

    for (i=0;i<n-2;i++)
    {
        p = que.top();
        result += p.first;
        p.second.second = p.second.second + 1;
        p.first = p.second.first * (2*p.second.second + 1);
        que.pop();
        que.push(p);
    }

    cout<<result;
    return 0;
}

 

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define ULL unsigned long long

const LL mod_1=1e9+7;
const LL mod_2=998244353;

const double eps_1=1e-5;
const double eps_2=1e-10;

const int maxn=2e5+10;

LL a[maxn];
typedef pair<LL, pair<LL, LL> > par;
priority_queue<par,vector<par>,greater<par> > que;
par p;

int main()
{
    LL n,i,result=0;
    cin>>n;
    for (i=0;i<n;i++)
    {
        cin>>a[i];
        que.push( make_pair(a[i]*(2*2-1*1), make_pair(1,a[i]) ) );
        result += a[i];
    }

    for (i=0;i<n-2;i++)
    {
        p = que.top();
        result += p.first;
        p.second.first = p.second.first + 1;
        p.first = p.second.second * (2*p.second.first + 1);
        que.pop();
        que.push(p);
    }

    cout<<result;
    return 0;
}