"华为杯"华南理工大学程序设计竞赛(同步赛) H、K、M(还没写)题解
"华为杯"华南理工大学程序设计竞赛(同步赛)_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ (nowcoder.com)
H
对于没有处理特殊情况(Sppac 国国王 Capps 居住在此街道),DP很好想。对于一个点为根的子树,如果这个点不选,它的孩子都要选;如果这个点选,它的孩子可以选/不选。
f[d][1] += max(f[chi][0], f[chi][1]); f[d][0] += f[chi][1];
然后对于特殊情况,对于这条边,可以让这条边的两个点为0(除此之外没有变化使得值发生变化)。
需要执行:所有点依次转成根的操作。就是从原始设置的根节点开始往下遍历,从V的父节点U为根节点,变为V为根节点。
对于V子树以外的内容,就是U子树-V子树。
对于V=0:因为V=0,所以U=1,对于U子树-V子树,这种情况的V可以为0或者1,所以是
f[chi][0] + ( f1[d][1] - max(f[chi][0], f[chi][1]) )
f[chi][1] + max( ( f1[d][1] - max(f[chi][0], f[chi][1]) , f1[d][0] - f[chi][1] )
int root_use_1, root_use_0; for (int chi:child[d]) { root_use_1 = f1[d][1] - max(f[chi][0], f[chi][1]); root_use_0 = f1[d][0] - f[chi][1]; f1[chi][0] = f[chi][0] + root_use_1; f1[chi][1] = f[chi][1] + max(root_use_1, root_use_0); find_f1(chi); }
造样例,比如一些随机的图。我用cyaron。手写出每种一条边可以不用的情况。
找到一些能判断错误的方法,比如特殊情况的值(一条边可以两个点为0)肯定大于等于没有处理特殊情况的值。
事实上,当图的点=8,我就能找出我的错误代码跑出来的错误样例了。
1 8 1 2 2 3 2 4 2 8 4 5 4 6 4 7
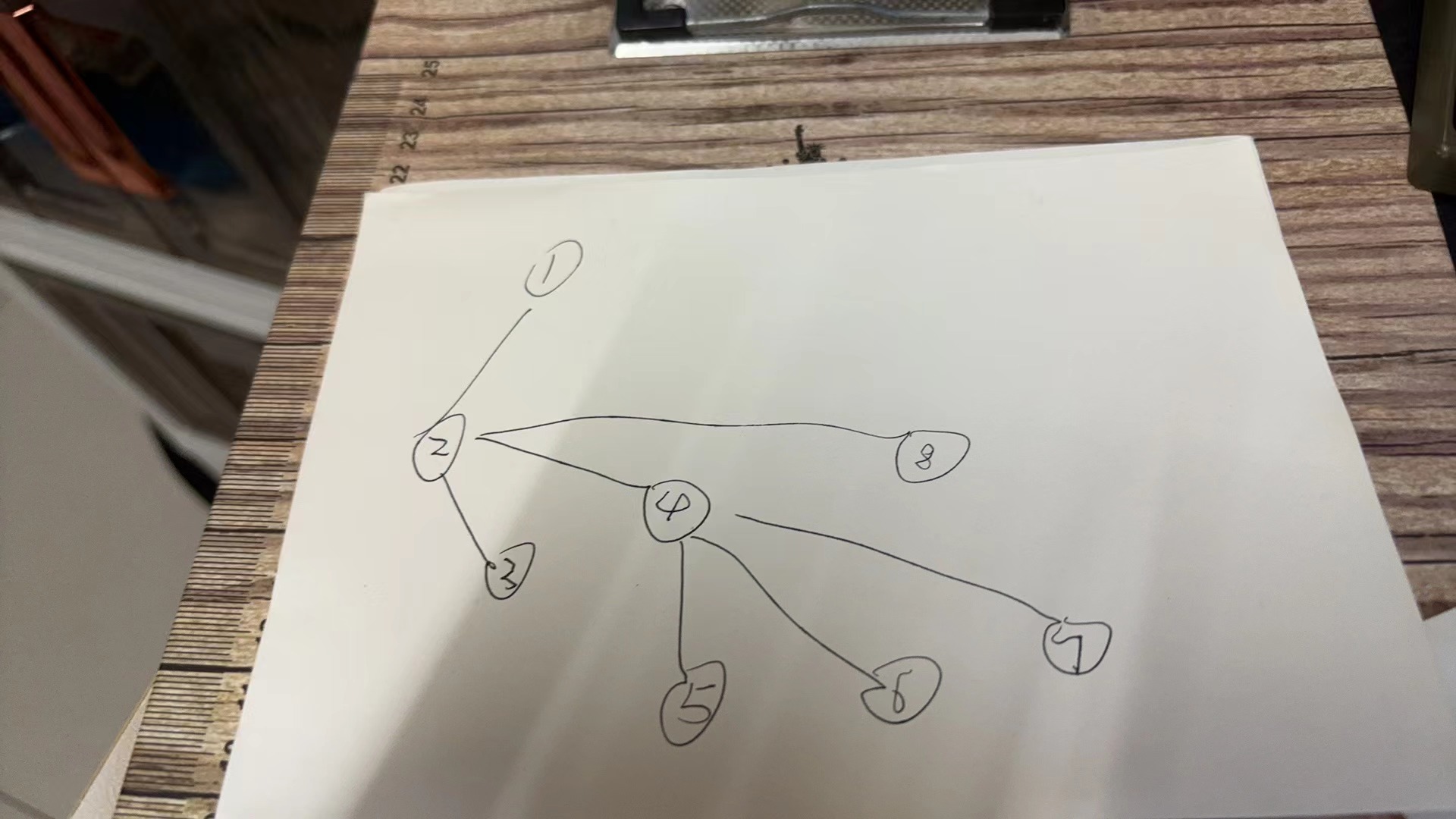
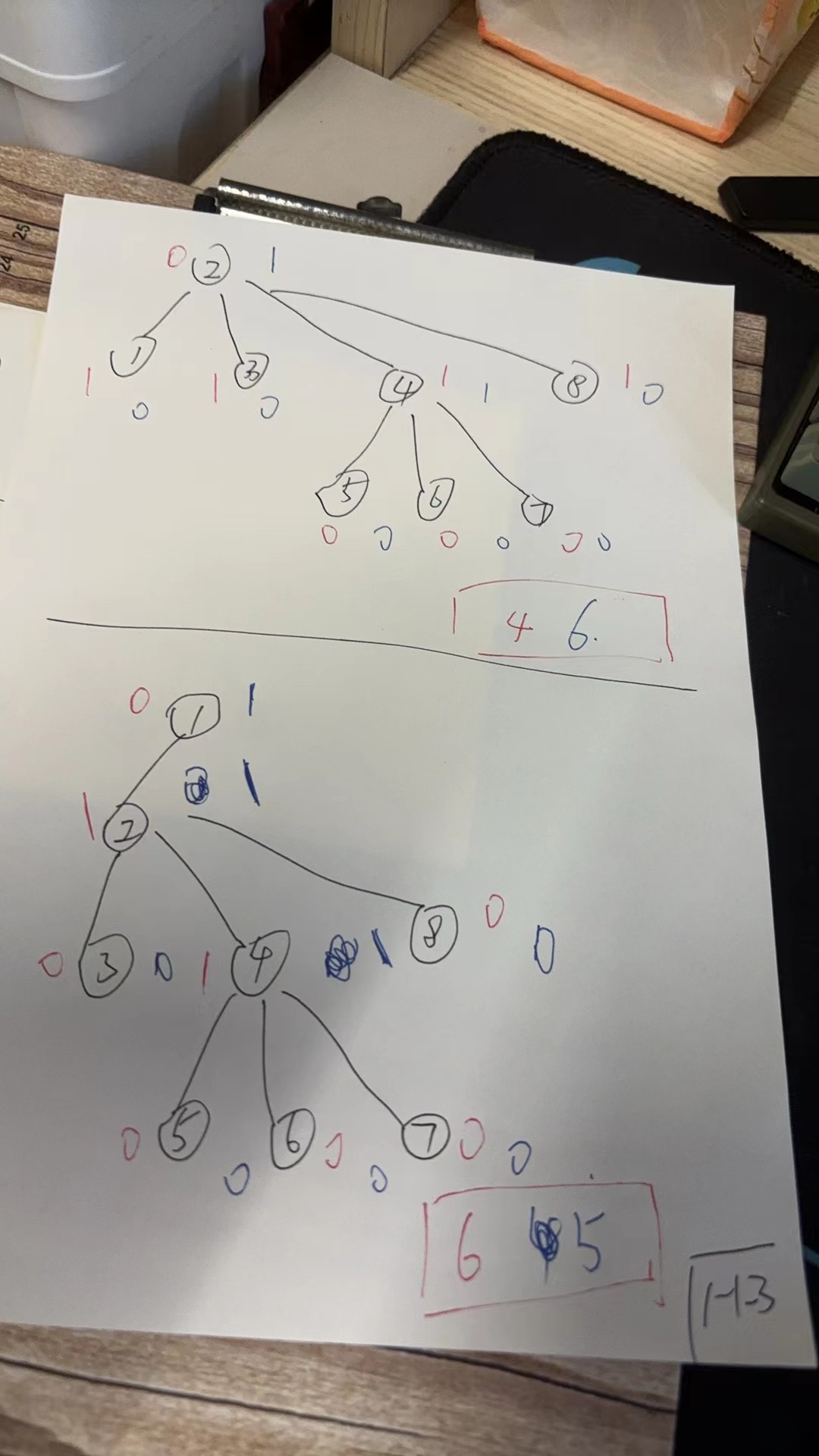
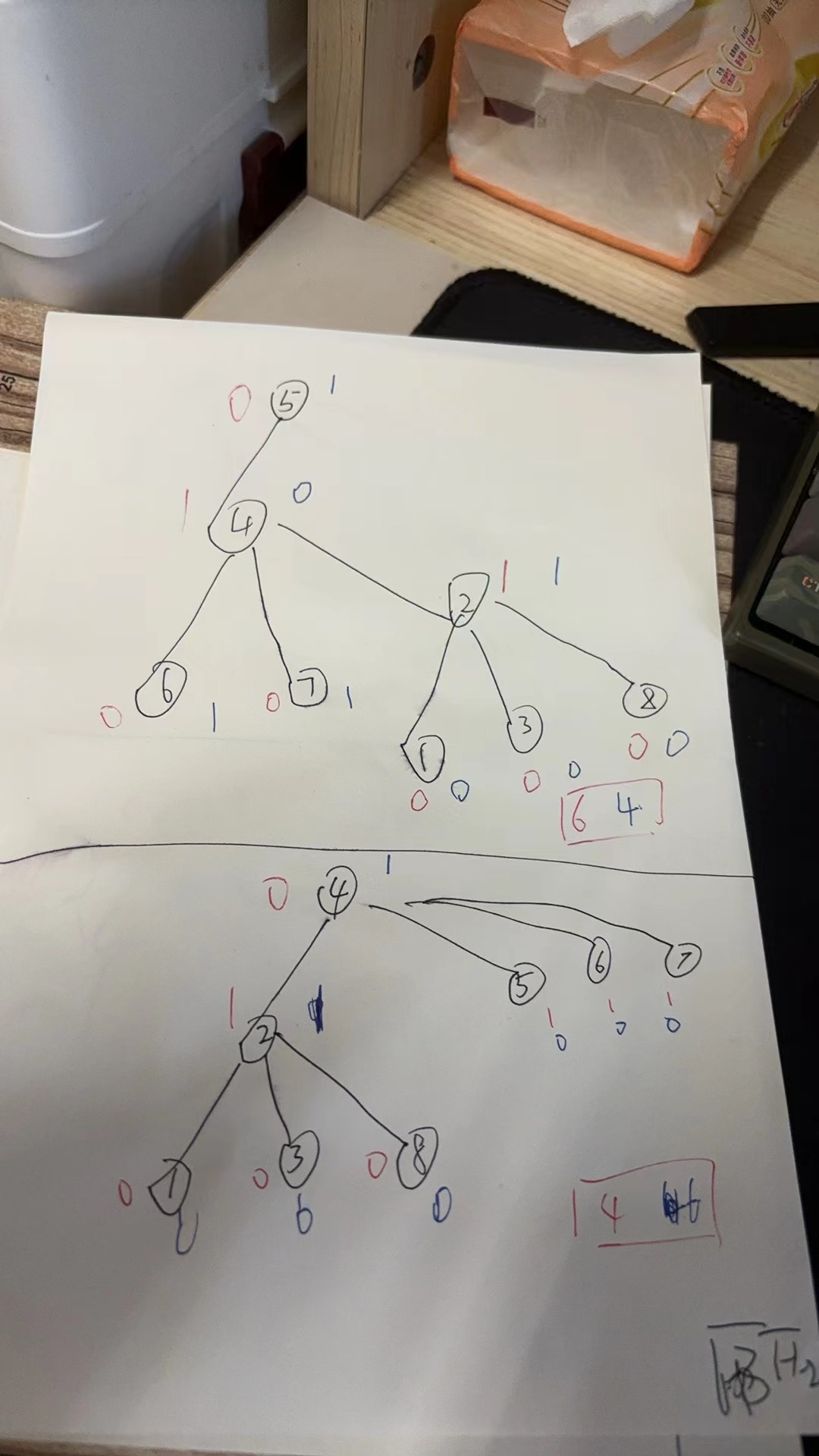
PS:如果写对拍的话,造比较小的样例,然后全部遍历找最大值,n个点,就是2^n(每个点只能01),然后乘上n-1条边就是2^n*(n-1),好写,2^20*20=20,971,520。
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cstring> 4 #include <cmath> 5 #include <stdbool.h> 6 #include <string> 7 #include <algorithm> 8 #include <iostream> 9 #include <sstream> 10 #include <ctime> 11 #include <stack> 12 #include <vector> 13 #include <queue> 14 #include <set> 15 #include <map> 16 using namespace std; 17 #define LL long long 18 19 const int maxn=4e5+10; 20 21 ///0 destroy ; 1 remain, has this point 22 23 24 int a[maxn], fa[maxn], edge[maxn][2]; 25 int f[maxn][2], f1[maxn][2], result[maxn]; 26 vector<int> adj[maxn],child[maxn]; 27 bool vis[maxn]; 28 29 void dfs(int d) 30 { 31 vis[d]=1; 32 f[d][0]=1; 33 f[d][1]=0; 34 for (int chi:adj[d]) 35 if (!vis[chi]) 36 { 37 dfs(chi); 38 child[d].push_back(chi); 39 fa[chi]=d; 40 41 f[d][1] += max(f[chi][0], f[chi][1]); 42 f[d][0] += f[chi][1]; 43 } 44 } 45 46 void find_f1(int d) 47 { 48 int root_use_1, root_use_0; 49 for (int chi:child[d]) 50 { 51 root_use_1 = f1[d][1] - max(f[chi][0], f[chi][1]); 52 root_use_0 = f1[d][0] - f[chi][1]; 53 f1[chi][0] = f[chi][0] + root_use_1; 54 f1[chi][1] = f[chi][1] + max(root_use_1, root_use_0); 55 56 find_f1(chi); 57 } 58 59 ///max(f[1][0],f[1][1]) 加了这个居然提高了 60 61 for (int chi:child[d]) 62 { 63 64 result[chi] = max(f1[d][1], f1[d][0] + max(0, f[chi][0] - f[chi][1]) ) ; 65 66 ///test ====== 67 68 //result[chi] = max( max(f[1][0],f[1][1]), max(f1[d][1], f1[d][0] + max(0, f[chi][0] - f[chi][1]) ) ); 69 /* 70 if (result[chi] < max(f[1][0],f[1][1])) 71 { 72 cout<<"wrong child "<<chi<<endl; 73 exit(-1); ///是存在这种情况的 74 } 75 */ 76 } 77 78 } 79 80 int main() 81 { 82 int T,n,i,x,y,chi; 83 scanf("%d",&T); 84 while (T--) 85 { 86 scanf("%d",&n); 87 for (i=1;i<=n;i++) 88 { 89 adj[i].clear(); 90 child[i].clear(); 91 vis[i]=0; 92 fa[i]=0; 93 f[i][0]=0, f[i][1]=0, f1[i][0]=0, f1[i][1]=0; 94 } 95 96 for (i=1;i<n;i++) 97 { 98 scanf("%d%d",&x,&y); 99 adj[x].push_back(y); 100 adj[y].push_back(x); 101 edge[i][0]=x, edge[i][1]=y; 102 } 103 104 dfs(1); 105 106 f1[1][0]=f[1][0]; 107 f1[1][1]=f[1][1]; 108 find_f1(1); 109 110 for (i=1;i<n;i++) 111 { 112 if (fa[ edge[i][0] ] == edge[i][1]) 113 chi = edge[i][0]; 114 else 115 chi = edge[i][1]; 116 117 cout << result[chi]; 118 if (i==n-1) 119 cout<<endl; 120 else 121 cout<<" "; 122 } 123 } 124 125 return 0; 126 } 127 /* 128 129 wrong 130 131 1 132 8 133 1 2 134 2 3 135 2 4 136 2 8 137 4 5 138 4 6 139 4 7 140 141 142 ====== 143 144 1 145 5 146 1 3 147 2 3 148 4 5 149 4 1 150 151 ====== 152 153 1 154 6 155 2 4 156 2 6 157 1 2 158 3 5 159 3 4 160 161 ====== 162 163 1 164 7 165 2 3 166 3 5 167 1 6 168 4 2 169 7 5 170 6 5 171 172 ====== 173 174 10 175 176 177 ====== 178 179 1 180 2 181 2 1 182 183 result:2 184 185 ====== 186 187 1 188 6 189 1 6 190 5 6 191 3 5 192 4 3 193 2 1 194 195 ====== 196 197 2 198 6 199 1 6 200 5 6 201 3 5 202 4 3 203 2 1 204 5 205 1 2 206 2 3 207 2 4 208 1 5 209 210 ====== 211 212 4 213 6 214 1 6 215 5 6 216 3 5 217 4 3 218 2 1 219 5 220 1 2 221 2 3 222 2 4 223 1 5 224 6 225 1 6 226 5 6 227 3 5 228 4 3 229 2 1 230 5 231 1 2 232 2 3 233 2 4 234 1 5 235 236 ====== 237 238 */
K
第一眼看题有点线段树的感觉。但是数值为x的数的位置,是离散的。
那么数值为x的数,用一个数据结构统计起来,然后op=1,2需要修改(删除和增加)和查找(删除的位置在哪),那么需要查找、删除、添加,都<=logn的复杂度。
set的查找和删除都是logn,而且set是unique结构,每次都排好序。
对于op=1,a[x]=y a[x]->a[x]+1,a[x]这个数的集合发生变化。
对于op=2,数值为x的集合合并到数值为x+1的集合。 这个操作是选择保留大的堆(大小大的堆),把小堆的内容移到大堆。
还有因为多数据,一些初始化的时间复杂度需要注意。
写这种题,变量比较乱,变量名要写清楚。首先是写清楚变量名的意思,其次是变量名是好辨认。
(还有一些操作可以合并写的,就合并写。)
1 /* 2 num_pos: a[x]这个数在哪个set里 3 set_value: 这个set对应是保存数值为多少的集合 4 set_pos: 数值为y的集合,在哪个set里 5 */ 6 #include <cstdio> 7 #include <cstdlib> 8 #include <cstring> 9 #include <cmath> 10 #include <string> 11 #include <algorithm> 12 #include <iostream> 13 #include <set> 14 #include <vector> 15 using namespace std; 16 #define LL long long 17 const int maxn=6e5+10; 18 19 set<int> s[maxn]; 20 int set_pos[maxn], num_pos[maxn],set_value[maxn]; 21 set<int> need_clean_set; 22 23 int main() 24 { 25 int test_cout=0; 26 27 int T,n,Q,op,x,size_1,size_2,has_1,has_2,i,cnt,xori,xadd,set_index; 28 scanf("%d",&T); 29 while (T--) 30 { 31 scanf("%d%d",&n,&Q); 32 cnt=1; 33 for (i=1;i<=n;i++) 34 { 35 s[1].insert(i); 36 num_pos[i]=1; 37 } 38 set_pos[0]=1; 39 set_value[1]=0; 40 need_clean_set.insert(1); 41 42 while (Q--) 43 { 44 scanf("%d%d",&op,&x); 45 if (op==1) 46 { 47 set_index = num_pos[x]; 48 xori = set_value[ set_index ]; 49 s[ set_index ].erase( s[ set_index ].find(x) ); 50 xadd = xori + 1; 51 if (set_pos[ xadd ]==0) 52 { 53 cnt++; 54 set_pos[ xadd ] = cnt; 55 set_value[ cnt ] = xadd; 56 } 57 s[ set_pos[xadd] ].insert(x); 58 num_pos[x] = set_pos[ xadd ]; 59 60 need_clean_set.insert(set_pos[ xori ]); 61 need_clean_set.insert(set_pos[ xadd ]); 62 } 63 else 64 { 65 has_1 = (set_pos[x]!=0); 66 has_2 = (set_pos[x+1]!=0); 67 68 size_1 = s[ set_pos[x] ].size(); 69 size_2 = s[ set_pos[x+1] ].size(); 70 71 if (has_1!=0) 72 { 73 if (has_2==0) 74 { 75 cnt++; 76 set_pos[ x+1 ] = cnt; 77 set_value[ cnt ] = x+1; 78 } 79 80 need_clean_set.insert(set_pos[ x ]); 81 need_clean_set.insert(set_pos[ x+1 ]); 82 83 if (size_1>size_2) 84 { 85 for (int d : s[ set_pos[x+1] ]) 86 { 87 s[ set_pos[x] ].insert(d); 88 num_pos[d] = set_pos[x]; 89 } 90 set_pos[x+1]=set_pos[x]; 91 set_pos[x]=0; 92 set_value[ set_pos[x+1] ] = x+1; 93 } 94 else 95 { 96 for (int d : s[ set_pos[x] ]) 97 { 98 s[ set_pos[x+1] ].insert(d); 99 num_pos[d] = set_pos[x+1]; 100 } 101 102 set_pos[x]=0; 103 } 104 } 105 } 106 } 107 108 if (test_cout) 109 cout<<"test begin"<<endl; 110 for (i=1;i<=n;i++) 111 { 112 cout<<set_value[ num_pos[i] ]; 113 if (i==n) 114 cout<<endl; 115 else 116 cout<<" "; 117 } 118 119 if (test_cout) 120 cout<<"test end"<<endl; 121 122 int temp=2*max(n,Q); 123 for (i=1;i<=temp;i++) 124 { 125 set_pos[i]=0; 126 set_value[i]=0; 127 num_pos[i]=0; 128 } 129 for (int set_index:need_clean_set) 130 s[set_index].clear(); 131 } 132 133 return 0; 134 } 135 /* 136 137 100 138 3 9 139 1 1 140 1 1 141 1 1 142 1 2 143 1 2 144 1 2 145 2 3 146 2 4 147 2 3 148 149 150 ====== 151 152 153 154 ====== 155 156 157 ====== 158 159 160 ====== 161 162 */
1 ///TLE 2 /* 3 num_pos: a[x]这个数在哪个set里 4 set_value: 这个set对应是保存数值为多少的集合 5 set_pos: 数值为y的集合,在哪个set里 6 */ 7 8 /* 9 如果想改为这个两个变量的话, 10 对于op=2,数值为y的数都需要修改。 11 而对于用num_pos,则大堆不需要修改 12 13 14 15 num_value: 下标为x的数,当前的数值 16 set_pos: 数值为y的集合,在哪个set里 17 */ 18 19 #include <cstdio> 20 #include <cstdlib> 21 #include <cstring> 22 #include <cmath> 23 #include <string> 24 #include <algorithm> 25 #include <iostream> 26 #include <set> 27 #include <vector> 28 using namespace std; 29 #define LL long long 30 const int maxn=6e5+10; 31 32 set<int> s[maxn]; 33 int num_value[maxn], set_pos[maxn]; 34 set<int> need_clean_set; 35 36 int main() 37 { 38 int test_cout=0; 39 40 int T,n,Q,op,x,size_1,size_2,i,cnt,yori,ynew,set_ori_index,set_new_index; 41 scanf("%d",&T); 42 memset(set_pos, 0, sizeof(set_pos)); 43 while (T--) 44 { 45 scanf("%d%d",&n,&Q); 46 cnt=1; 47 for (i=1;i<=n;i++) 48 { 49 s[1].insert(i); 50 num_value[i]=0; 51 } 52 set_pos[0]=1; 53 54 need_clean_set.insert(1); 55 56 while (Q--) 57 { 58 scanf("%d%d",&op,&x); 59 if (op==1) 60 { 61 yori = num_value[x]; 62 set_ori_index = set_pos[ yori ]; 63 s[ set_ori_index ].erase( s[ set_ori_index ].find(x) ); 64 ynew = yori + 1; 65 num_value[x] = ynew; 66 if (set_pos[ ynew ]==0) 67 { 68 cnt++; 69 set_pos[ ynew ] = cnt; 70 } 71 set_new_index = set_pos[ ynew ]; 72 s[ set_new_index ].insert(x); 73 74 need_clean_set.insert( set_ori_index ); 75 need_clean_set.insert( set_new_index ); 76 } 77 else 78 { 79 set_ori_index = set_pos[x]; 80 set_new_index = set_pos[x+1]; 81 size_1 = s[ set_ori_index ].size(); 82 size_2 = s[ set_new_index ].size(); 83 84 ///op=2 保证有元素。 -> 这样不用判断了。 size_1>0,那么size_2=0,也可以处理的 85 86 need_clean_set.insert( set_ori_index ); 87 need_clean_set.insert( set_new_index ); 88 89 if (size_1>size_2) 90 { 91 for (int d : s[ set_new_index ]) 92 s[ set_ori_index ].insert(d); 93 for (int d : s[ set_ori_index ]) 94 num_value[d] = x+1; 95 96 set_pos[x+1]=set_pos[x]; 97 set_pos[x]=0; 98 } 99 else 100 { 101 for (int d : s[ set_ori_index ]) 102 { 103 s[ set_new_index ].insert(d); 104 num_value[d] = x+1; 105 } 106 set_pos[x]=0; 107 } 108 } 109 } 110 111 if (test_cout) 112 cout<<"test begin"<<endl; 113 for (i=1;i<=n;i++) 114 { 115 cout<<num_value[i]; 116 if (i==n) 117 cout<<endl; 118 else 119 cout<<" "; 120 } 121 122 if (test_cout) 123 cout<<"test end"<<endl; 124 125 int temp=2*max(n,Q); ///每次操作,最大数值和需要修改的set数都最多增加1。但*2,保险一点 126 for (i=1;i<=temp;i++) 127 { 128 num_value[i]=0; 129 set_pos[i]=0; 130 } 131 for (int set_ori_index:need_clean_set) 132 s[set_ori_index].clear(); 133 } 134 135 return 0; 136 } 137 /* 138 139 100 140 3 9 141 1 1 142 1 1 143 1 1 144 1 2 145 1 2 146 1 2 147 2 3 148 2 4 149 2 3 150 151 152 ====== 153 154 155 156 ====== 157 158 159 ====== 160 161 162 ====== 163 164 */
M
这题意很好懂,总感觉过去见过类似的题。



