拉格朗日插值
study from
https://blog.csdn.net/Code92007/article/details/94412729
P5050 【模板】多项式多点求值
各种神仙常数优化、NTT
1.常数优化(来自洛谷题解)

学习了!
O2优化 g++某些版本
循环展开:并行操作
http://blog.miskcoo.com/2015/05/polynomial-multipoint-eval-and-interpolation
但还是超时了
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cmath> 4 #include <cstring> 5 #include <string> 6 #include <algorithm> 7 #include <iostream> 8 using namespace std; 9 #define ull unsigned long long 10 #define R register 11 12 const double eps=1e-8; 13 const ull inf=1e9; 14 const ull mod=998244353; 15 const int maxn=1e5+10; 16 17 ull a[maxn],b[17]; ///can not use as constant 18 19 inline void read(R ull &y) 20 { 21 char ch=getchar(); 22 y=0; 23 while (ch<'0' || ch>'9') 24 ch=getchar(); 25 while (ch>='0' && ch<='9') 26 y=y*10+ch-48,ch=getchar(); 27 } 28 29 char pr[10]; 30 int cnt; 31 inline void write(R ull &y) 32 { 33 cnt=0; 34 while (y) 35 { 36 pr[++cnt]=y%10+48; 37 y/=10; 38 } 39 for (R int i=cnt;i;i--) 40 putchar(pr[i]); 41 putchar('\n'); 42 } 43 44 int main() 45 { 46 R ull n,m,x,y,c1,c2,c3,c4; 47 R int i; 48 read(n),read(m); 49 for (i=0;i<=n;i++) 50 read(a[i]); 51 while (m--) 52 { 53 read(x); 54 b[0]=1; 55 for (i=1;i<=16;i++) 56 b[i]=b[i-1]*x%mod; 57 y=0; 58 for (i=n;i>=15;i-=16) 59 { 60 ///998244353^2*16 15,943,868,612,742,217,744 61 ///unsigned long long 1.8e19 62 c1=a[i]*b[15]+a[i-1]*b[14]+a[i-2]*b[13]+a[i-3]*b[12]; 63 c2=a[i-4]*b[11]+a[i-5]*b[10]+a[i-6]*b[9]+a[i-7]*b[8]; 64 c3=a[i-8]*b[7]+a[i-9]*b[6]+a[i-10]*b[5]+a[i-11]*b[4]; 65 c4=a[i-12]*b[3]+a[i-13]*b[2]+a[i-14]*b[1]+a[i-15]; 66 y=(c1+c2+c3+c4+y*b[16])%mod; 67 } 68 for (;i>=0;i--) 69 y=(y*x+a[i])%mod; 70 write(y); 71 } 72 return 0; 73 } 74 /* 75 20 3 76 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 77 2 1 3 78 */
原始代码
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cmath> 4 #include <cstring> 5 #include <string> 6 #include <algorithm> 7 #include <iostream> 8 using namespace std; 9 #define ll long long 10 11 const double eps=1e-8; 12 const ll inf=1e9; 13 const ll mod=998244353; 14 const int maxn=1e5+10; 15 16 ll a[maxn]; 17 18 inline void read(ll &y) 19 { 20 char ch=getchar(); 21 y=0; 22 while (ch<'0' || ch>'9') 23 ch=getchar(); 24 while (ch>='0' && ch<='9') 25 y=y*10+ch-48,ch=getchar(); 26 } 27 28 int main() 29 { 30 int n,m,i; 31 ll x,y,z; 32 scanf("%d%d",&n,&m); 33 for (i=0;i<=n;i++) 34 read(a[i]); 35 while (m--) 36 { 37 read(x); 38 y=0; 39 z=1; 40 for (i=0;i<=n;i++) 41 { 42 (y+=a[i]*z)%=mod; 43 z=z*x%mod; 44 } 45 printf("%lld\n",y); 46 } 47 return 0; 48 }
P4781 【模板】拉格朗日插值
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cmath> 4 #include <cstring> 5 #include <string> 6 #include <algorithm> 7 #include <iostream> 8 using namespace std; 9 #define ll long long 10 11 const double eps=1e-8; 12 const ll inf=1e9; 13 const ll mod=998244353; 14 const int maxn=2e3+10; 15 16 ll a[maxn],x[maxn],y[maxn]; 17 18 ll mul(ll a,ll b) 19 { 20 ll y=1; 21 while (b) 22 { 23 if (b&1) 24 y=y*a%mod; 25 a=a*a%mod; 26 b>>=1; 27 } 28 return y; 29 } 30 31 int main() 32 { 33 ll i,j,n,d,tot,sum=0,u,v; 34 scanf("%lld%lld",&n,&d); 35 for (i=0;i<n;i++) 36 scanf("%lld%lld",&x[i],&y[i]); 37 ///n*n 38 ///multiply n-1 numbers 39 for (i=0;i<n;i++) 40 { 41 ///can also multiply n numbers and divide one number 42 u=1; 43 for (j=0;j<n;j++) 44 if (i!=j) 45 u=u*(d-x[j])%mod; 46 47 v=1; 48 for (j=0;j<n;j++) 49 if (i!=j) 50 v=v*(x[i]-x[j])%mod; 51 52 tot=y[i]*u%mod; 53 if (v<0) 54 tot=-tot,v=-v; 55 56 (sum+=tot*mul(v,mod-2)%mod)%=mod; 57 } 58 printf("%lld\n",(sum+mod)%mod); 59 return 0; 60 } 61 /* 62 3 4 63 1 4 64 2 9 65 3 16 66 */
https://loj.ac/problem/166
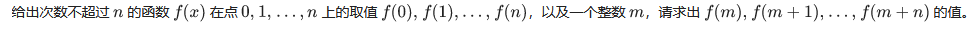
P5158 【模板】多项式快速插值
之后再补
===============================
自然数幂和
https://codeforces.com/problemset/problem/622/F
F. The Sum of the k-th Powers
k+1次函数的证明
1.
“差分” 牛顿插值多项式
(from https://www.bbsmax.com/A/RnJWLeoE5q/)
2.
不同方法 https://blog.csdn.net/werkeytom_ftd/article/details/50741165
其中的分治fft棒棒的!
伯努利数 https://blog.csdn.net/cj1064789374/article/details/85388995
斯特林数 https://blog.csdn.net/lyd_7_29/article/details/75041818
若干个k次函数相加为k+1次函数
ai
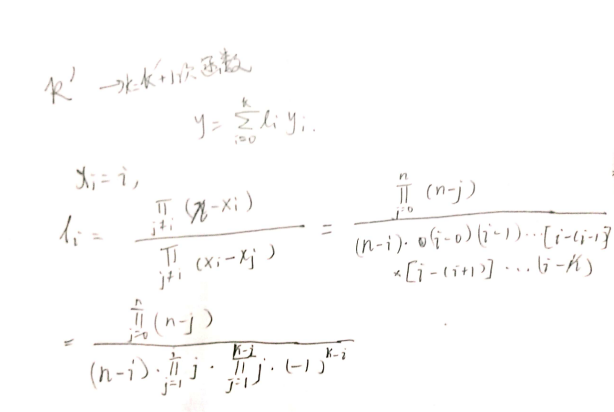
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cmath> 4 #include <cstring> 5 #include <string> 6 #include <algorithm> 7 #include <iostream> 8 using namespace std; 9 #define ll long long 10 11 const double eps=1e-8; 12 const ll inf=1e9; 13 const ll mod=1e9+7; 14 const int maxn=1e6+10; 15 16 ll y[maxn],a[maxn],jie[maxn],inv_jie[maxn]; 17 18 ll mul(ll a,ll b) 19 { 20 ll y=1; 21 while (b) 22 { 23 if (b&1) 24 y=y*a%mod; 25 a=a*a%mod; 26 b>>=1; 27 } 28 return y; 29 } 30 31 int main() 32 { 33 ll n,k,i,u,tot,sum=0; 34 scanf("%lld%lld",&n,&k); 35 k++; 36 for (i=1;i<=k;i++) 37 y[i]=(y[i-1]+mul(i,k-1))%mod; /// 38 if (n<=k) 39 { 40 printf("%lld",y[n]); 41 return 0; 42 } 43 44 u=1; 45 for (i=n;i>=n-k;i--) 46 u=u*i%mod; 47 48 jie[0]=1; 49 for (i=1;i<=k;i++) 50 jie[i]=jie[i-1]*i%mod; 51 inv_jie[k]=mul(jie[k],mod-2); 52 for (i=k-1;i>=0;i--) /// 53 inv_jie[i]=inv_jie[i+1]*(i+1)%mod; 54 55 for (i=0;i<=k;i++) 56 { 57 tot=inv_jie[i]*inv_jie[k-i]%mod *u%mod *mul(n-i,mod-2)%mod; 58 if ((k-i)&1) 59 tot=-tot; 60 (sum+=tot*y[i])%=mod; 61 } 62 printf("%lld",(sum+mod)%mod); 63 return 0; 64 } 65 /* 66 1 10 67 10 1 68 10 2 69 10 3 70 */
另外的题目
The 2019 ICPC China Nanchang National Invitational and International Silk-Road Programming Contest
https://www.cnblogs.com/cmyg/p/11255754.html
BZOJ2665
BZOJ4559


 浙公网安备 33010602011771号
浙公网安备 33010602011771号