FTT & NTT & 分治FFT

 

 

FFT

study from:

http://www.orchidany.cf/2019/02/19/FFT1/

https://www.cnblogs.com/zwfymqz/p/8244902.html

e^iθ=cosθ+isinθ

 

重新写了一遍……

 

A(x)=F(x)*G(x)

F(x),G(x),A(x)分别为n,m,n+m次多项式

对于任意x，A(x),F(x),G(x)都是一个特定的数值。

 

F(x),G(x)为什么可以进行系数表示法和点值表示法的互换?

因为它们是k次多项式，如使用拉格朗日插值多项式从点值表示法转换为系数表示法。

对于A(x)，同样也是如此！

 

为什么可以进行F(x)*G(x)点值的相乘呢？

1.无论x为多少，A(x)都等于F(x)*G(x)

2.A(x)可以用点值表示，它是n+m次多项式（感觉说了句无用的话）

 

那需要多少个F(x)和G(x)点值的相乘呢？

由于A(x)是n+m次多项式，则F(x),G(x)至少各需要n+m+1个点值

 

得到的是n+m+1个点值，然后点值表示法转系数表示法，求出A(x)这个n+m次多项式的所有系数。

 

 

关于蝴蝶操作（迭代实现）

最后的编号（一种规则）->起始

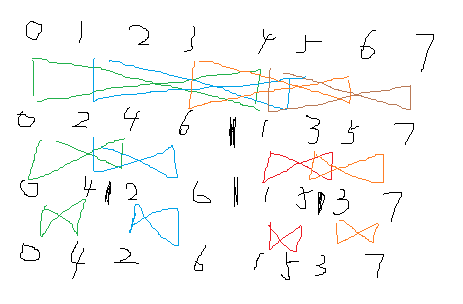
两个位置在原位置上的改动

 

区间1->2->4->...

 

P3803 【模板】多项式乘法（FFT）

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <string>
#include <algorithm>
#include <iostream>
using namespace std;
#define ll long long

const double eps=1e-8;
const ll inf=1e9;
const ll mod=1e9+7;
const int maxn=(1e6+10)*4; ///注意乘4[(n+m)*2]
const double pi=acos(-1);

struct complex
{
    double x,y;
    complex()
    {
    }
    complex(double x,double y)
    {
        this->x=x;
        this->y=y;
    }
    void init(double x,double y)
    {
        this->x=x;
        this->y=y;
    }
    complex operator+(const complex &b) const
    {
        return complex(x+b.x , y+b.y);
    }
    complex operator-(const complex &b) const
    {
        return complex(x-b.x , y-b.y);
    }
    complex operator*(const complex &b) const
    {
        return complex(x*b.x-y*b.y , x*b.y+y*b.x);
    }
}a[maxn],b[maxn];

int r[maxn],n,m,tot;

void fft(complex a[maxn],int mode)
{
    int i,j,pre_siz,cur_siz;
    complex temp,value,x,y;
    for (i=0;i<tot;i++)
        if (i<r[i]) ///just change one time
            swap(a[i],a[r[i]]);

    for (pre_siz=1;pre_siz<tot;pre_siz<<=1)
    {
        cur_siz=pre_siz<<1;
        /// 2pi/cur_siz = pi/pre_siz
        temp.init(cos(pi/pre_siz),mode*sin(pi/pre_siz));
        for (i=0;i<tot;i+=cur_siz)
        {
            value.init(1,0);
            for (j=0;j<pre_siz;j++,value=value*temp)
            {
                x=a[i+j],y=value*a[i+pre_siz+j];
                a[i+j]=x+y;
                a[i+pre_siz+j]=x-y;
            }
        }
    }
}

int main()
{
    int i,nm,len;
    scanf("%d%d",&n,&m);
    for (i=0;i<=n;i++)
        scanf("%lf",&a[i].x);
    for (i=0;i<=m;i++)
        scanf("%lf",&b[i].x);

    nm=n+m;
    tot=1,len=0;
    while (tot<=nm)  ///2^len not less than n+m+1
    {
        tot<<=1;
        len++;
    }

    ///关系 ......
    for (i=0;i<tot;i++)
        r[i]=(r[i>>1]>>1) | ((i&1)<<(len-1));

    ///系数表示法转点值表示法
    fft(a,1);
    fft(b,1);

    ///a,b点值相乘
    for (i=0;i<tot;i++)
        a[i]=a[i]*b[i];

    ///点值表示法转系数表示法，恰巧为......
    fft(a,-1);

    for (i=0;i<=nm;i++) ///n+m
        ///点值表示法转系数表示法，要除以的系数
        printf("%lld%c",(ll)(a[i].x/tot+0.5),i==tot?'\n':' ');  /// /tot


    return 0;
}

 

P1919 【模板】A*B Problem升级版（FFT快速傅里叶）

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <string>
#include <algorithm>
#include <iostream>
using namespace std;
#define ll long long

const double eps=1e-8;
const ll inf=1e9;
const ll mod=1e9+7;
const int maxn=(1e6+10)*4; ///注意乘4[(n+m)*2]
const double pi=acos(-1);

struct complex
{
    double x,y;
    complex()
    {
    }
    complex(double x,double y)
    {
        this->x=x;
        this->y=y;
    }
    void init(double x,double y)
    {
        this->x=x;
        this->y=y;
    }
    complex operator+(const complex &b) const
    {
        return complex(x+b.x , y+b.y);
    }
    complex operator-(const complex &b) const
    {
        return complex(x-b.x , y-b.y);
    }
    complex operator*(const complex &b) const
    {
        return complex(x*b.x-y*b.y , x*b.y+y*b.x);
    }
}a[maxn],b[maxn];

int r[maxn],n,m,tot,z[maxn];

char str[maxn];

void fft(complex a[maxn],int mode)
{
    int i,j,pre_siz,cur_siz;
    complex temp,value,x,y;
    for (i=0;i<tot;i++)
        if (i<r[i]) ///just change one time
            swap(a[i],a[r[i]]);

    for (pre_siz=1;pre_siz<tot;pre_siz<<=1)
    {
        cur_siz=pre_siz<<1;
        /// 2pi/cur_siz = pi/pre_siz
        temp.init(cos(pi/pre_siz),mode*sin(pi/pre_siz));
        for (i=0;i<tot;i+=cur_siz)
        {
            value.init(1,0);
            for (j=0;j<pre_siz;j++,value=value*temp)
            {
                x=a[i+j],y=value*a[i+pre_siz+j];
                a[i+j]=x+y;
                a[i+pre_siz+j]=x-y;
            }
        }
    }
}

int main()
{
    int i,nm,len;
    scanf("%d",&n); ///输入样例有毒，n后面有空格
    n--;

    scanf("%s",str);
    for (i=0;i<=n;i++)
        a[n-i].x=str[i]-48;

    scanf("%s",str);
    for (i=0;i<=n;i++)
        b[n-i].x=str[i]-48;

    nm=n+n;
    tot=1,len=0;
    while (tot<=nm)  ///2^len not less than n+m+1
    {
        tot<<=1;
        len++;
    }

    ///关系 ......
    for (i=0;i<tot;i++)
        r[i]=(r[i>>1]>>1) | ((i&1)<<(len-1));

    ///系数表示法转点值表示法
    fft(a,1);
    fft(b,1);

    ///a,b点值相乘
    for (i=0;i<tot;i++)
        a[i]=a[i]*b[i];

    ///点值表示法转系数表示法，恰巧为......
    fft(a,-1);

    for (i=0;i<=nm;i++)
    {
        ///点值表示法转系数表示法，要除以的系数
        z[i]+=a[i].x/tot+0.5;
//        printf("%d ",a[i].x/tot+0.5);
        if (z[i]>=10)
        {
            z[i+1]+=z[i]/10;
            z[i]%=10;
        }
        else if (z[i]<0)
        {
            z[i+1]+=z[i]/10-(z[i]!=0);
            z[i]=(z[i]%10+10)%10;
        }
    }
    while (z[i]>=10)
    {
        z[i+1]=z[i]/10;
        z[i]%=10;
        i++;
    }

    ///输入的都是正整数
    ///前导0
    while (z[i]==0)
        i--;

    while (i>=0)
        printf("%d",z[i--]);

    ///也可以认为结果是a[0]+a[1]*10+a[2]*10^2+...


    return 0;
}
/*
2
12
13

2
99
99

3
199
299


10
9789344841
4839019669



另外的提高速度的方法：
压位

结果为：
a[0]+a[1]*x+a[2]*x^2
x=10^k

*/

 

==================================================

 

NTT

https://www.cnblogs.com/Wuweizheng/p/8553155.html

百度“原根”

 

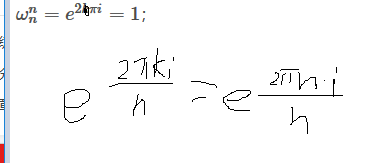
 对于选取的P，可用的n最大的值与P中的2的系数有关

 

如选择998244353就优于1004535809。

如果选择框住的三个数，那么可以处理的最大的n+m为2^23=8388608。

最好模数对应的g(底数，最后一列)都相同，否则对于不同的模数，要选择不同的g。

 

如果题目要求除以998244353之类的满足条件的数，则可以直接用这个方法做，不用后续处理

 

P1919 【模板】A*B Problem升级版（FFT快速傅里叶）

结果小于等于

9[第一个数每一位的最大值]*9[第二个数每一位的最大值]*n[两个数的最大长度] = 4860000

可以使用取模998244353

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <string>
#include <algorithm>
#include <iostream>
using namespace std;
#define ll long long

const double eps=1e-8;
const ll inf=1e9;
const ll mod=998244353;
const int maxn=(1e5+10)*4;

ll di=3;
int tot,r[maxn];
ll a[maxn],b[maxn],inv_siz[100],inv_rev_siz[100],c[maxn];

char str[maxn];

ll mul(ll a,ll b)
{
    ll y=1;
    while (b)
    {
        if (b&1)
            y=y*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return y;
}

void ntt(ll a[maxn],int mode)
{
    int i,j,cnt_pre,cnt_cur,siz;
    ll x,y,sing,value;
    for (i=0;i<tot;i++)
        if (i<r[i])
            swap(a[i],a[r[i]]);

    for (cnt_pre=1,siz=1;cnt_pre<tot;cnt_pre=cnt_pre<<1,siz++)  ///
    {
        cnt_cur=cnt_pre<<1;
        sing=mode==1?inv_siz[siz]:inv_rev_siz[siz];
        for (i=0;i<tot;i+=cnt_cur)
        {
            value=1;
            for (j=0;j<cnt_pre;j++,value=value*sing%mod)
            {
                x=a[i+j],y=value*a[i+j+cnt_pre]%mod;
                a[i+j]=(x+y)%mod;
                a[i+j+cnt_pre]=(x-y+mod)%mod;
            }
        }
    }
}

int main()
{
    int n,m,len,nm,i,j;
 64 //    scanf("%d%d%d",&n,&m,&p);
//    for (i=0;i<=n;i++)
//        scanf("%lld",&a[i]);
//    for (i=0;i<m;i++)
//        scanf("%lld",&b[i]);

    scanf("%d",&n);
    n--;

    scanf("%s",str);
    for (i=0;i<=n;i++)
        a[i]=str[n-i]-48;

    scanf("%s",str);
    for (i=0;i<=n;i++)
        b[i]=str[n-i]-48;

    nm=n+n;
    tot=1,len=0;
    while (tot<=nm)
    {
        tot<<=1;
        len++;
    }
    for (i=1;i<tot;i++)
        r[i]=(r[i>>1]>>1) | ((i&1)<<(len-1));
    for (i=2,j=1;i<=tot;i=i<<1,j++) ///
    {
        inv_siz[j]=mul(di,(mod-1)/i);
        inv_rev_siz[j]=mul(di,(mod-1)-(mod-1)/i);
    }


    ntt(a,1);
    ntt(b,1);
    for (i=0;i<tot;i++)
        a[i]=a[i]*b[i]%mod;
    ntt(a,-1);
    j=mul(tot,mod-2);
    for (i=0;i<=nm;i++)
    {
        a[i]=a[i]*j%mod;

        c[i]+=a[i];
        if (c[i]>=10)
        {
            c[i+1]+=c[i]/10;
            c[i]%=10;
        }
        else if (c[i]<0)
        {
            c[i+1]+=c[i]/10-(c[i]!=0);
            c[i]=(c[i]%10+10)%10;
        }
    }
    while (c[i]>=10)
    {
        c[i+1]=c[i]/10;
        c[i]%=10;
        i++;
    }

    while (c[i]==0)
        i--;
    while (i>=0)
        printf("%lld",c[i--]);


    return 0;
}
/*
1
8
9

2
12
13

2
99
99

3
111
111

3
999
102

101898
*/

感觉别人的代码短很多：

https://www.bbsmax.com/A/ke5jRWmO5r/

mode=-1下不同的实现方法

reverse(&a[1],&a[limit]);

 

P4245 【模板】任意模数NTT

https://www.luogu.org/problemnew/solution/P4245

https://www.cnblogs.com/Memory-of-winter/p/10223844.html

 

这样写的前提是取模的数之间互质，才能使用inv(模数) [inv 指的是 求逆]

 

可以理解为k1''=k1'+g*B

x1+k1''A=x1+(k1'+g*B)*A=(x1+k1'*A)+g*A*B

 

======================================

 

max = 10^9 * 10^9 * 10^5 = 10^23

对应若干个模数的相等大于它

 

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <string>
#include <algorithm>
#include <iostream>
using namespace std;
#define ll long long

const double eps=1e-8;
const ll inf=1e9;
const int maxn=(1e5+10)*4;

ll chu[3]={998244353,469762049,167772161};  ///single>10^8 all>10^24
ll di=3,mod,re[3][maxn];
int tot,r[maxn];
ll a[maxn],b[maxn],aa[maxn],bb[maxn],inv_siz[100],inv_rev_siz[100],c[maxn];

ll mul(ll a,ll b)
{
    ll y=1;
    while (b)
    {
        if (b&1)
            y=y*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return y;
}

ll _mul(ll a,ll b,ll c)
{
    ll y=1;
    while (b)
    {
        if (b&1)
            y=y*a%c;
        a=a*a%c;
        b>>=1;
    }
    return y;
}

void ntt(ll a[maxn],int mode)
{
    int i,j,cnt_pre,cnt_cur,siz;
    ll x,y,sing,value;
    for (i=0;i<tot;i++)
        if (i<r[i])
            swap(a[i],a[r[i]]);

    for (cnt_pre=1,siz=1;cnt_pre<tot;cnt_pre=cnt_pre<<1,siz++)  ///
    {
        cnt_cur=cnt_pre<<1;
        sing=mode==1?inv_siz[siz]:inv_rev_siz[siz];
        for (i=0;i<tot;i+=cnt_cur)
        {
            value=1;
            for (j=0;j<cnt_pre;j++,value=value*sing%mod)
            {
                x=a[i+j],y=value*a[i+j+cnt_pre]%mod;
                a[i+j]=(x+y)%mod;
                a[i+j+cnt_pre]=(x-y+mod)%mod;
            }
        }
    }
}

int main()
{
    int n,m,len,nm,i,j,k;
    ll p;
    scanf("%d%d%lld",&n,&m,&p);
    for (i=0;i<=n;i++)
    {
        scanf("%lld",&aa[i]);
        aa[i]%=p;
    }
    for (i=0;i<=m;i++)
    {
        scanf("%lld",&bb[i]);
        bb[i]%=p;
    }

    nm=n+m;
    tot=1,len=0;
    while (tot<=nm)
    {
        tot<<=1;
        len++;
    }
    for (i=1;i<tot;i++)
        r[i]=(r[i>>1]>>1) | ((i&1)<<(len-1));
    for (k=0;k<3;k++)
    {
        memcpy(a,aa,sizeof(aa));
        memcpy(b,bb,sizeof(bb));
        ///最主要觉得一起写在ntt函数中，不好改

        mod=chu[k];
        for (i=2,j=1;i<=tot;i=i<<1,j++) ///
        {
            inv_siz[j]=mul(di,(mod-1)/i);
            inv_rev_siz[j]=mul(di,(mod-1)-(mod-1)/i);
        }

        ntt(a,1);
        ntt(b,1);
        for (i=0;i<tot;i++)
            a[i]=a[i]*b[i]%mod;
        ntt(a,-1);
        j=mul(tot,mod-2);
        for (i=0;i<=nm;i++)
            re[k][i]=a[i]*j%mod;

    }

    /**
    取模的数之间，gcd(mod1,mod2)=1
    **/
    ll x1,x2,x3,x4,A,B,C,k1,k4;
    for (j=0;j<=nm;j++)
    {
        x1=re[0][j],x2=re[1][j],x3=re[2][j];
        A=chu[0],B=chu[1],C=chu[2];
        k1=(((x2-x1)%B+B)%B)*_mul(A,B-2,B)%B;
        x4=x1+k1*A;
        k4=(((x3-x4)%C+C)%C)*_mul(A*B%C,C-2,C)%C;   ///(...%C+C)%C
        printf("%lld%c",(x4%p+k4%p*A%p*B%p)%p,j==nm?'\n':' '); ///k4%p, since k4>p
        ///it is safe that x4%p
        ///之后则是((x4-x5+D)%D)*mul(A*B%D*C%D,D-2,D)%D;
    }
    return 0;
}
/*
1 1 10001
1000000000 1000000000
1000000000 1000000000

1 2 10001
1000000000 1000000000
1000000000 1000000000 1000000000

5 6 1000000009
1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
*/

 

看毛啸《再探快速傅里叶变换》

 

题目练习：

[SDOI2015]序列统计

 

 

==================================================

 

分治FFT

P4721 【模板】分治 FFT

https://blog.csdn.net/VictoryCzt/article/details/82939586

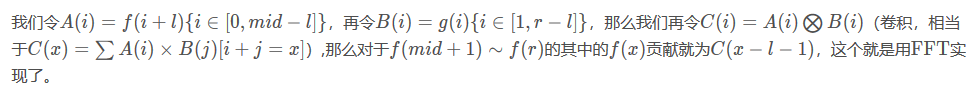
其实，C(x)是多算了一些内容，C(0)~C(mid-l-1)是无用的，但是没办法。

(r-mid)+(r-mid-1)+...+1 -> FFT len=大于等于r-l的最小的数，O(len*log(len))。

 

对于f(x) 其它数1-~x-1对f(x)的贡献，

通过cdq处理

类似的题 https://www.cnblogs.com/cmyg/p/11146038.html

 

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <string>
#include <algorithm>
#include <iostream>
using namespace std;
#define ll long long

const double eps=1e-8;
const ll inf=1e9;
const ll mod=998244353;
const int maxn=(1e5+10)*4;

ll f[maxn],g[maxn],a[maxn],b[maxn];
ll inv_di[100],inv_rev_di[100],inv_tot[100];
int tot,ind[maxn];
ll di=3;

ll mul(ll a,ll b)
{
    ll y=1;
    while (b)
    {
        if (b&1)
            y=y*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return y;
}

void ntt(ll *a,int mode)
{
    int i,j,cnt_pre,cnt_cur,cnt=0;
    ll sing,value,x,y;
    for (i=0;i<tot;i++)
        if (i<ind[i])
            swap(a[i],a[ind[i]]);
    for (cnt_pre=1,cnt=1;cnt_pre<tot;cnt_pre<<=1,cnt++)
    {
        cnt_cur=cnt_pre<<1;
        sing=mode==1?inv_di[cnt]:inv_rev_di[cnt];
        for (i=0;i<tot;i+=cnt_cur)
        {
            value=1;
            for (j=0;j<cnt_pre;j++,value=value*sing%mod)
            {
                x=a[i+j],y=a[i+j+cnt_pre]*value%mod;
                a[i+j]=(x+y)%mod;
                a[i+j+cnt_pre]=(x-y+mod)%mod;
            }
        }
    }
}

void cdq(int l,int r)
{
    if (l==r)
        return;

    int m=(l+r)>>1,nm,len,i;
    cdq(l,m);

    /**
    对于[m+1,r],
    [l,m]对它们的贡献
    C(z)=f(l+x)*g(1+y)
    x in [0,m-l]
    y in [0,r-l-1]

    z=x+y
    [m-l,r-l-1]
    **/

    tot=1,len=0;
    nm=(m-l)+(r-l-1);
    while (tot<=nm)
        tot<<=1,len++;
    for (i=1;i<tot;i++)
        ind[i]=(ind[i>>1]>>1) | ((i&1)<<(len-1));
    for (i=0;i<=m-l;i++)
        a[i]=f[l+i];
    for (i=m-l+1;i<tot;i++)
        a[i]=0;
    for (i=0;i<=r-l-1;i++)
        b[i]=g[1+i];
    for (i=r-l;i<tot;i++)
        b[i]=0;
    ntt(a,1);
    ntt(b,1);
    for (i=0;i<tot;i++)
        a[i]=a[i]*b[i]%mod;
    ntt(a,-1);

    for (i=m-l;i<=r-l-1;i++)
        (f[i+l+1]+=a[i]*inv_tot[len])%=mod;

    cdq(m+1,r);
}

int main()
{
    int n,i,j;
    scanf("%d",&n);
    for (i=1;i<n;i++)
        scanf("%lld",&g[i]);
    f[0]=1;

    for (i=1,j=0;i<=4e5;i<<=1,j++)
    {
        inv_tot[j]=mul(i,mod-2);
        inv_di[j]=mul(di,(mod-1)/i);
        inv_rev_di[j]=mul(di,(mod-1)-(mod-1)/i);
    }

    cdq(0,n);   ///begin from 0
    for (i=0;i<n;i++)
        printf("%lld%c",f[i],i==n-1?'\n':' ');
    return 0;
}

 

快速沃尔什变换 与 快速莫比乌斯变换
https://www.cnblogs.com/cmyg/p/10424145.html