贝壳找房魔法师顾问 2018 计蒜之道 复赛
https://nanti.jisuanke.com/t/A1725
V&V
无向图
强连通图
每个子图,n个点,选择n-1条,使互相连接
因为目标点x->点y,可以改为点y->点x
V&C
弱连通图(将有向图的所有的有向边替换为无向边,所得到的图称为原图的基图。如果一个有向图的基图是连通图,则有向图是弱连通图。)
1.一个弱连通子图,它里面的点与该弱连通子图外的点与没有关系,可以单独处理
2.弱连通子图里,一个点,必有另外点与之相邻,包括入和出
3.若弱连通子图里有环,则无论怎么修改,避免不了最后的图,有环的情况(因为需求无法改变,x指向y,则从x出发,必有路径到y),
对于环外剩下的点,也必至少有一条边,总边数大于等于点数
4.对于弱连通子图的点,可以构造一个环,使它们相互可以到达,需要的边的数量为点数
5.所以对于有环的弱连通子图,选择4的方案,构造环
6.对于没有环的弱连通子图,求拓扑排序,从小到大赋予编号,
按照编号,点1连接,点2连接点3,...,点p-1连接点p,满足条件。
对于边,必定是编号小的点连接编号大的点,所以没有产生遗漏。
需要的边的数量为点数-1
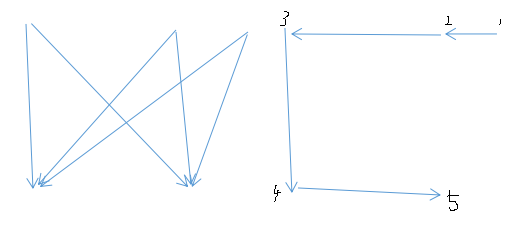
如
6
Constant 1 2 3 1 2 3
Variable 4 4 4 5 5 5
计蒜客好像不能开以下优化,差评:
ios_base::sync_with_stdio(0);
cin.tie(0);
///所以参加比赛时,先测试一下这些能不能用
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cmath> 4 #include <cstring> 5 #include <string> 6 #include <algorithm> 7 #include <iostream> 8 using namespace std; 9 #define ll long long 10 #include <map> 11 12 const double eps=1e-8; 13 const ll inf=1e9; 14 const ll mod=1e9+7; 15 const int maxn=1e5+10; 16 17 struct node 18 { 19 int d; 20 node *to; 21 }*e[maxn],*b[maxn]; 22 23 string c[2]; 24 int s[2][maxn],tot[maxn],q[maxn]; 25 bool vis[maxn]; 26 27 map<pair<int,int>,int> ma; 28 29 int main() 30 { 31 // ios_base::sync_with_stdio(0); 32 // cin.tie(0); 33 34 node *p; 35 int n,i,j,k,x,y,cnt=0; 36 int head,tail,d,temp; 37 scanf("%d",&n); 38 k=0; 39 for (j=0;j<2;j++) 40 { 41 cin>>c[j]; 42 if (j==0 && c[0][0]=='C') 43 k=1; 44 45 for (i=1;i<=n;i++) 46 cin>>s[j^k][i]; 47 } 48 if (k==1) 49 swap(c[0],c[1]); 50 51 if (c[0][0]=='C' && c[1][0]=='C') 52 { 53 for (i=1;i<=n;i++) 54 if (s[0][i]!=s[1][i]) 55 break; 56 if (i==n+1) 57 cout<<0; 58 else 59 cout<<-1; 60 } 61 else if (c[1][0]=='C') 62 { 63 for (i=1;i<=n;i++) 64 { 65 x=s[0][i]; 66 y=s[1][i]; 67 if (x==y || ma.find({x,y})!=ma.end()) 68 continue; 69 ma[{x,y}]=1; 70 p=new node(); 71 p->d=y; 72 p->to=e[x]; 73 e[x]=p; 74 75 p=new node(); 76 p->d=x; 77 p->to=e[y]; 78 e[y]=p; 79 tot[y]++; 80 81 p=new node(); 82 p->d=y; 83 p->to=b[x]; 84 b[x]=p; 85 86 } 87 88 for (i=1;i<=1e5;i++) 89 if (!vis[i] && e[i]) 90 { 91 q[1]=i; 92 vis[i]=1; 93 head=0,tail=1; 94 while (head<tail) 95 { 96 d=q[++head]; 97 p=e[d]; 98 while (p) 99 { 100 if (!vis[p->d]) 101 { 102 vis[p->d]=1; 103 q[++tail]=p->d; 104 } 105 p=p->to; 106 } 107 } 108 109 temp=tail; 110 head=0,tail=0; 111 for (j=1;j<=temp;j++) 112 if (!tot[q[j]]) 113 q[++tail]=q[j]; 114 115 ///if no loop, traversal tail points 116 while (head<tail) 117 { 118 head++; 119 d=q[head]; 120 p=b[d];/// 121 while (p) 122 { 123 tot[p->d]--; 124 if (!tot[p->d]) 125 q[++tail]=p->d; 126 p=p->to; 127 } 128 } 129 cnt+=temp-(tail==temp); 130 } 131 cout<<cnt; 132 } 133 else 134 { 135 for (i=1;i<=n;i++) 136 { 137 x=s[0][i]; 138 y=s[1][i]; 139 if (x==y) 140 continue; 141 p=new node(); 142 p->d=y; 143 p->to=e[x]; 144 e[x]=p; 145 146 p=new node(); 147 p->d=x; 148 p->to=e[y]; 149 e[y]=p; 150 } 151 152 for (i=1;i<=1e5;i++) 153 if (!vis[i] && e[i]) 154 { 155 q[1]=i; 156 vis[i]=1; 157 head=0,tail=1; 158 while (head<tail) 159 { 160 d=q[++head]; 161 p=e[d]; 162 while (p) 163 { 164 if (!vis[p->d]) 165 { 166 vis[p->d]=1; 167 q[++tail]=p->d; 168 } 169 p=p->to; 170 } 171 } 172 cnt+=tail-1; 173 } 174 cout<<cnt; 175 } 176 return 0; 177 } 178 /* 179 2 180 Constant 111 222 181 Constant 111 223 182 183 2 184 Constant 111 222 185 Constant 111 222 186 187 5 188 Variable 111 222 333 444 555 189 Variable 222 333 111 444 666 190 191 5 192 Constant 111 222 333 444 333 193 Variable 222 111 444 555 666 194 195 5 196 Variable 222 111 444 555 666 197 Constant 111 222 333 444 333 198 199 7 200 Variable 222 111 444 555 666 444 444 201 Constant 111 222 333 444 333 666 555 202 203 3 204 Variable 111 111 111 205 Variable 222 222 222 206 207 4 208 Constant 333 111 111 111 209 Variable 333 222 222 222 210 211 6 212 Constant 1 2 3 1 2 3 213 Variable 4 4 4 5 5 5 214 215 6 216 Variable 1 2 3 1 2 3 217 Variable 4 4 4 5 5 5 218 219 3 220 Variable 1 2 3 221 Variable 4 5 6 222 223 3 224 Constant 1 2 3 225 Variable 4 5 6 226 */



