网络流进阶

study from:

一篇很好的文章拆点拆边

https://www.cnblogs.com/tweetuzki/p/10422496.html

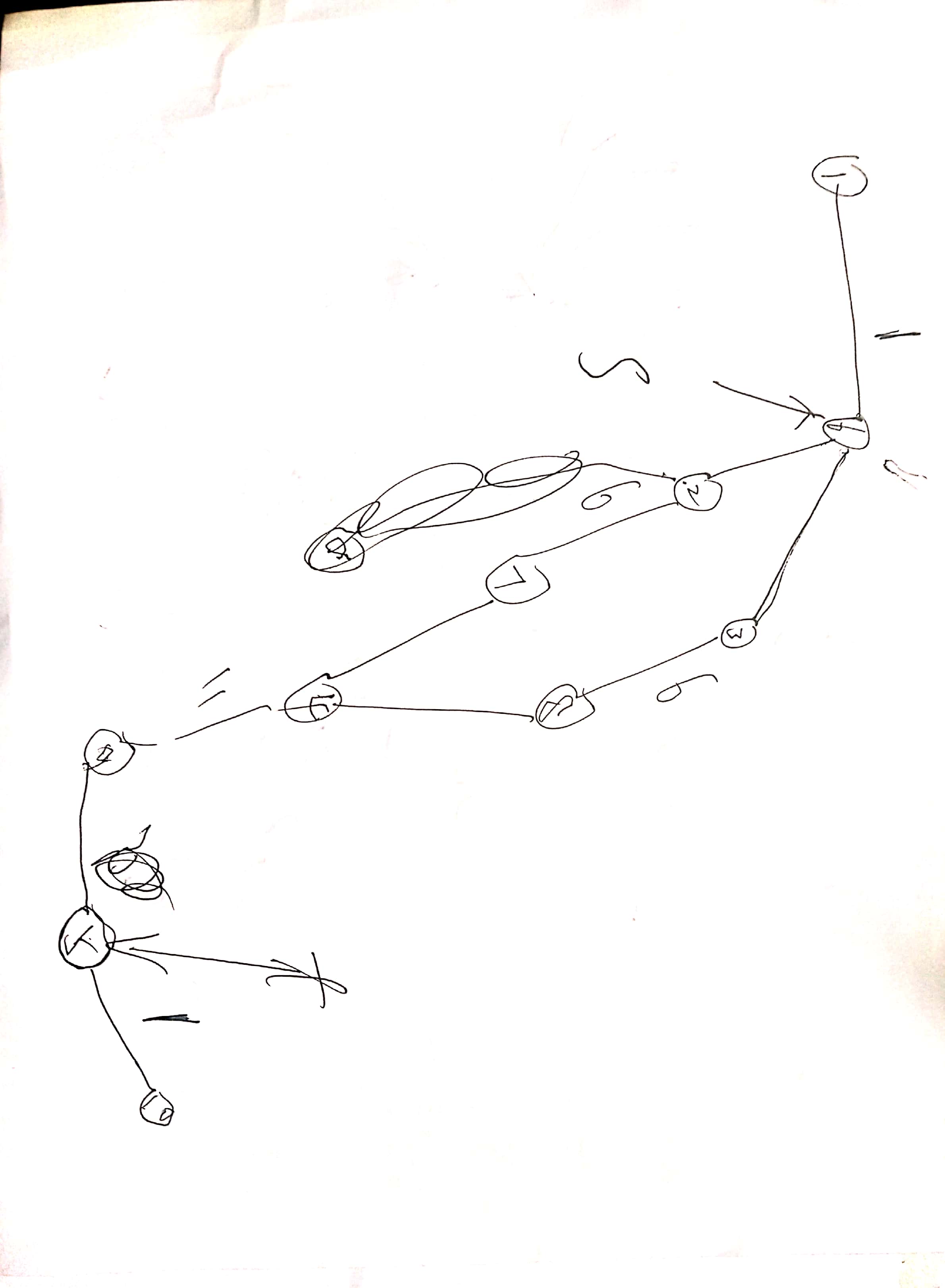
认真看解释，造一个简单、有代表性的图，画图辅助理解

Thieves

http://acm.hdu.edu.cn/showproblem.php?pid=3491

最小割=最大流

拆点(点有流量限制)

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cstring>
  4 #include <string>
  5 #include <cmath>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10 
 11 const int maxn=1e4+10;
 12 const int inf=1e9;
 13 
 14 struct node
 15 {
 16     int d,len;
 17     node *to,*opp;
 18 }*e[maxn];
 19 
 20 int s,t,q[maxn],dep[maxn];
 21 
 22 void addedge(int x,int y,int z)
 23 {
 24     node *p1,*p2;
 25     p1=new node();
 26     p2=new node();
 27 
 28     p1->d=y;
 29     p1->len=z;
 30     p1->opp=p2;
 31     p1->to=e[x];
 32     e[x]=p1;
 33 
 34     p2->d=x;
 35     p2->len=0;
 36     p2->opp=p1;
 37     p2->to=e[y];
 38     e[y]=p2;
 39 }
 40 
 41 bool bfs()
 42 {
 43     node *p;
 44     int head=0,tail=1,d,dd;
 45     memset(dep,0,sizeof(dep));
 46     dep[s]=1;
 47     q[1]=s;
 48     while (head<tail)
 49     {
 50         head++;
 51         d=q[head];
 52         p=e[d];
 53         while (p)
 54         {
 55             dd=p->d;
 56             if (!dep[dd] && p->len)
 57             {
 58                 q[++tail]=dd;
 59                 dep[dd]=dep[d]+1;
 60             }
 61             p=p->to;
 62         }
 63     }
 64     if (dep[t])
 65         return 1;
 66     return 0;
 67 }
 68 
 69 int dfs(int d,int add)
 70 {
 71     if (!add || d==t)
 72         return add;
 73     int totr=0,r,dd;
 74     node *p=e[d];
 75     while (p)
 76     {
 77         dd=p->d;
 78         if (dep[dd]==dep[d]+1 && (r=dfs(dd,min(add,p->len)))>0)
 79         {
 80             totr+=r;
 81             add-=r;
 82             p->len-=r;
 83             p->opp->len+=r;
 84         }
 85         p=p->to;
 86     }
 87     return totr;
 88 }
 89 
 90 int main()
 91 {
 92     int T,n,m,x,y,i,v,sum;
 93     scanf("%d",&T);
 94     while (T--)
 95     {
 96         scanf("%d%d%d%d",&n,&m,&s,&t);
 97         s+=n;
 98 //        t+=n;
 99         for (i=1;i<=2*n;i++)
100             e[i]=0;
101         for (i=1;i<=n;i++)
102         {
103             scanf("%d",&v);
104             addedge(i,i+n,v);
105         }
106         while (m--)
107         {
108             scanf("%d%d",&x,&y);
109             addedge(x+n,y,inf);
110             addedge(y+n,x,inf);
111         }
112         sum=0;
113         while (bfs())
114             sum+=dfs(s,inf);
115         printf("%d\n",sum);
116     }
117     return 0;
118 }

类似的题目

Dining

http://poj.org/problem?id=3281

https://nanti.jisuanke.com/t/A1106

菜鸟物流的运输网络

way1

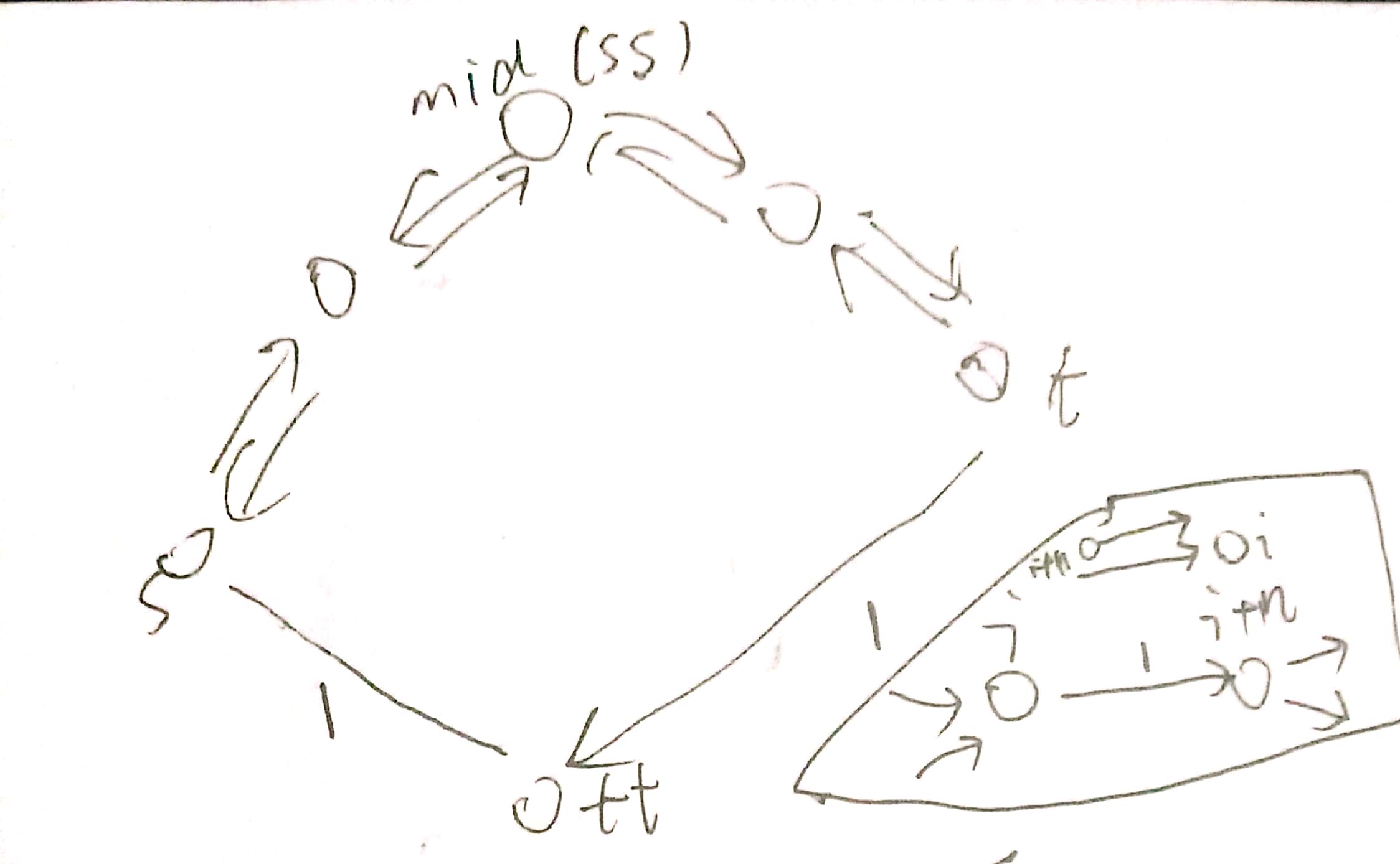
拆点，点i连点i+n，流量为1，从原点i入的边连接i+n，从原点i出的边连接点i。

源点mid，超级汇点连接s,t。

need边取反，即只适用于双向边

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cstring>
  4 #include <string>
  5 #include <cmath>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10 #include <queue>
 11 const int maxn=2e2+10;///*2
 12 const int inf=1e9;
 13 #include <assert.h>
 14 
 15 struct node
 16 {
 17     int d,len,cond;
 18     node *to,*opp;
 19 }*e[maxn];
 20 
 21 int n,ss,tt,mid,q[maxn],dep[maxn];
 22 
 23 void addedge(int x,int y,int z)
 24 {
 25     node *p1,*p2;
 26     p1=new node();
 27     p2=new node();
 28 
 29     p1->d=y;
 30     p1->len=z;
 31     p1->opp=p2;
 32     p1->to=e[x];
 33     e[x]=p1;
 34     p1->cond=0;
 35 
 36     p2->d=x;
 37     p2->len=0;
 38     p2->opp=p1;
 39     p2->to=e[y];
 40     e[y]=p2;
 41     p2->cond=1;
 42 }
 43 
 44 bool bfs()
 45 {
 46     node *p;
 47     int head=0,tail=1,d,dd;
 48     memset(dep,0,sizeof(dep));
 49     dep[ss]=1;
 50     q[1]=ss;
 51     while (head<tail)
 52     {
 53         head++;
 54         d=q[head];
 55         p=e[d];
 56         while (p)
 57         {
 58             dd=p->d;
 59             if (!dep[dd] && p->len)
 60             {
 61                 q[++tail]=dd;
 62                 dep[dd]=dep[d]+1;
 63             }
 64             p=p->to;
 65         }
 66     }
 67     if (dep[tt])
 68         return 1;
 69     return 0;
 70 }
 71 
 72 int dfs(int d,int add)
 73 {
 74 //    printf("%d %d\n",d,add);
 75     if (!add || d==tt)
 76         return add;
 77     int totr=0,r,dd;
 78     node *p=e[d];
 79     while (p)
 80     {
 81         dd=p->d;
 82         if (dep[dd]==dep[d]+1 && (r=dfs(dd,min(add,p->len)))>0)
 83         {
 84             totr+=r;
 85             add-=r;
 86             p->len-=r;
 87             p->opp->len+=r;
 88         }
 89         p=p->to;
 90     }
 91     return totr;
 92 }
 93 
 94 void print(int x)
 95 {
 96     node *p=e[x];
 97     while (p)
 98     {
 99         if (p->cond && p->len)
100         {
101             x=p->d;
102             if (x!=mid)
103                 print(x);
104             break;
105         }
106         p=p->to;
107     }
108     if (x<=n)
109         printf("%d ",x);
110 }
111 
112 int main()
113 {
114     node *p;
115     int T,m,x,y,i,s,t,sum;
116     scanf("%d",&T);
117     while (T--)
118     {
119         scanf("%d%d",&n,&m);
120         scanf("%d%d%d",&s,&t,&mid);
121         ss=2*n+1;
122         tt=2*n+2;
123         for (i=1;i<=2*n+2;i++)
124             e[i]=0;
125         for (i=1;i<=n;i++)
126             if (i==mid)
127                 addedge(i,i+n,2);
128             else
129                 addedge(i,i+n,1);
130         addedge(2*n+1,mid,2);
131         addedge(s+n,2*n+2,1);
132         addedge(t+n,2*n+2,1);
133         while (m--)
134         {
135             scanf("%d%d",&x,&y);
136             addedge(x+n,y,1);
137             addedge(y+n,x,1);
138         }
139 
140         sum=0;
141         while (bfs())
142             sum+=dfs(ss,inf);
143 
144         x=s;
145         while (x!=mid)
146         {
147             if (x<=n)
148                 printf("%d ",x);
149             p=e[x];
150             while (p)
151             {
152                 if (p->cond && p->len)
153                 {
154                     x=p->d;
155                     break;
156                 }
157                 p=p->to;
158             }
159         }
160         print(t);
161         printf("%d\n",t);
162     }
163     return 0;
164 }
165 /*
166 4
167 
168 5 5
169 1 5 3
170 1 2
171 2 3
172 3 4
173 4 5
174 5 1
175 
176 5 5
177 1 3 5
178 1 2
179 2 3
180 3 4
181 4 5
182 5 1
183 
184 3 3
185 1 2 3
186 2 1
187 2 3
188 3 1
189 
190 4 6
191 2 1 4
192 1 2
193 1 3
194 1 4
195 2 3
196 2 4
197 3 4
198 
199 10 10
200 5 3 10
201 1 2
202 2 3
203 3 4
204 4 5
205 5 6
206 6 7
207 7 8
208 8 9
209 9 10
210 10 1
211 
212 3 0
213 1 2 3
214 */

若求最短路径，用费用流。

但仍需要拆点，见以下情况。

同样的，不拆点求网络流，采用去环的方式也是不行的，见以下情况。

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cstring>
  4 #include <string>
  5 #include <cmath>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10 #include <queue>
 11 const int maxn=2e2+10;///*2
 12 const int inf=1e9;
 13 #include <assert.h>
 14 
 15 /*
 16 时间复杂度为O(N*E*k)，其中K为最大流值。但时间上的期望时间复杂度为：O(A*E*K)，其中A为所有顶点进队列的平均次数，可以证明A一般小于等于2。
 17 */
 18 
 19 struct node
 20 {
 21     int d,len,cost,cond;
 22     node *to,*opp;
 23 }*e[maxn],*pre[maxn];
 24 
 25 int ss,tt,dist[maxn],add[maxn],flow,fee;
 26 bool vis[maxn];
 27 int ans_p,pr[maxn];
 28 
 29 queue<int>st;
 30 
 31 void addedge(int x,int y,int len,int cost)
 32 {
 33     node *p1,*p2;
 34     p1=new node();
 35     p2=new node();
 36 
 37     p1->d=y;
 38     p1->len=len;
 39     p1->cost=cost;
 40     p1->opp=p2;
 41     p1->to=e[x];
 42     p1->cond=0;
 43     e[x]=p1;
 44 
 45     p2->d=x;
 46     p2->len=0;
 47     p2->cost=-cost;
 48     p2->opp=p1;
 49     p2->to=e[y];
 50     p2->cond=1;
 51     e[y]=p2;
 52 }
 53 
 54 void bfs()
 55 {
 56     node *p;
 57     int d,dd;
 58     while (1)
 59     {
 60         memset(dist,0x7f,sizeof(dist));
 61         dist[ss]=0;
 62         add[ss]=inf;
 63         add[tt]=0;
 64 
 65         st.push(ss);
 66         while (!st.empty())
 67         {
 68             d=st.front();
 69             st.pop();
 70             p=e[d];
 71             while (p)
 72             {
 73                 dd=p->d;
 74                 if (p->len && dist[dd]>dist[d]+p->cost)
 75                 {
 76                     dist[dd]=dist[d]+p->cost;
 77                     add[dd]=min(add[d],p->len);
 78                     pre[dd]=p->opp;
 79                     if (!vis[dd])
 80                     {
 81                         vis[dd]=1;
 82                         st.push(dd);
 83                     }
 84                 }
 85                 p=p->to;
 86             }
 87             vis[d]=0;
 88         }
 89 
 90         if (add[tt]==0)
 91             break;
 92 
 93         flow+=add[tt];
 94         fee+=add[tt]*dist[tt];
 95         d=tt;
 96         while (d!=ss)
 97         {
 98             pre[d]->len+=add[tt];
 99             pre[d]->opp->len-=add[tt];
100             d=pre[d]->d;
101         }
102     }
103 }
104 
105 int main()
106 {
107     node *p;
108     int T,n,m,x,y,i,mid,s,t;
109     scanf("%d",&T);
110     while (T--)
111     {
112         scanf("%d%d",&n,&m);
113         scanf("%d%d%d",&s,&t,&mid);
114         ss=2*n+1;
115         tt=2*n+2;
116         for (i=1;i<=2*n+2;i++)
117             e[i]=0;
118         for (i=1;i<=n;i++)
119             if (i==mid)
120                 addedge(i,i+n,2,1);
121             else
122                 addedge(i,i+n,1,1);
123         addedge(2*n+1,mid,2,1);
124         addedge(s+n,2*n+2,1,1);
125         addedge(t+n,2*n+2,1,1);
126         while (m--)
127         {
128             scanf("%d%d",&x,&y);
129             addedge(x+n,y,1,1);
130             addedge(y+n,x,1,1);
131         }
132 
133         flow=0,fee=0;
134         bfs();
135 
136 //        printf("data=%d %d %d\n",s,t,mid);
137 
138         if (flow!=2)
139         {
140             printf("-1\n");
141             continue;
142         }
143 
144         ans_p=0;
145         x=s;
146         while (x!=mid)
147         {
148             if (x<=n)
149                 pr[++ans_p]=x;
150             p=e[x];
151             while (p)
152             {
153                 if (p->cond && p->len)
154                 {
155                     x=p->d;
156                     break;
157                 }
158                 p=p->to;
159             }
160         }
161         for (i=1;i<=ans_p;i++)
162             printf("%d ",pr[i]);
163 
164         ans_p=0;
165         x=t;
166         while (x!=mid)
167         {
168             if (x<=n)
169                 pr[++ans_p]=x;
170             p=e[x];
171             while (p)
172             {
173                 if (p->cond && p->len)
174                 {
175                     x=p->d;
176                     break;
177                 }
178                 p=p->to;
179             }
180         }
181         printf("%d",mid);
182         for (i=ans_p;i>=1;i--)
183             printf(" %d",pr[i]);
184         printf("\n");
185     }
186     return 0;
187 }
188 /*
189 5
190 
191 5 5
192 1 5 3
193 1 2
194 2 3
195 3 4
196 4 5
197 5 1
198 
199 5 5
200 1 3 5
201 1 2
202 2 3
203 3 4
204 4 5
205 5 1
206 
207 3 3
208 1 2 3
209 2 1
210 2 3
211 3 1
212 
213 4 6
214 2 1 4
215 1 2
216 1 3
217 1 4
218 2 3
219 2 4
220 3 4
221 
222 10 10
223 5 3 10
224 1 2
225 2 3
226 3 4
227 4 5
228 5 6
229 6 7
230 7 8
231 8 9
232 9 10
233 10 1
234 
235 3 0
236 1 2 3
237 
238 5 6
239 2 1 4
240 1 2
241 2 4
242 4 5
243 4 3
244 5 1
245 3 1
246 
247 */

错误代码1

网络流不拆点删环

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cstring>
  4 #include <string>
  5 #include <cmath>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10 #include <queue>
 11 const int maxn=1e2+10;
 12 const int inf=1e9;
 13 #include <assert.h>
 14 
 15 /*
 16 不拆点，网络规模减少一半
 17 
 18 输出结果，去环 O(n)
 19 或者用费用流 每条边cost=-1,求最短的路径
 20 费用流时间复杂度？
 21 dinic时间复杂度？
 22 */
 23 
 24 struct node
 25 {
 26     int d,len,cond,visit;
 27     node *to,*opp;
 28 }*e[maxn];
 29 
 30 int ss,tt,mid,q[maxn],dep[maxn];
 31 int ans_p,pr[maxn],pre[maxn];
 32 
 33 void addedge(int x,int y,int z)
 34 {
 35     node *p1,*p2;
 36     p1=new node();
 37     p2=new node();
 38 
 39     p1->d=y;
 40     p1->len=z;
 41     p1->opp=p2;
 42     p1->to=e[x];
 43     e[x]=p1;
 44     p1->cond=0;
 45 
 46     p2->d=x;
 47     p2->len=0;
 48     p2->opp=p1;
 49     p2->to=e[y];
 50     e[y]=p2;
 51     p2->cond=1;
 52 }
 53 
 54 bool bfs()
 55 {
 56     node *p;
 57     int head=0,tail=1,d,dd;
 58     memset(dep,0,sizeof(dep));
 59     dep[ss]=1;
 60     q[1]=ss;
 61     while (head<tail)
 62     {
 63         head++;
 64         d=q[head];
 65         p=e[d];
 66         while (p)
 67         {
 68             dd=p->d;
 69             if (!dep[dd] && p->len)
 70             {
 71                 q[++tail]=dd;
 72                 dep[dd]=dep[d]+1;
 73             }
 74             p=p->to;
 75         }
 76     }
 77     if (dep[tt])
 78         return 1;
 79     return 0;
 80 }
 81 
 82 int dfs(int d,int add)
 83 {
 84     if (!add || d==tt)
 85         return add;
 86     int totr=0,r,dd;
 87     node *p=e[d];
 88     while (p)
 89     {
 90         dd=p->d;
 91         if (dep[dd]==dep[d]+1 && (r=dfs(dd,min(add,p->len)))>0)
 92         {
 93             totr+=r;
 94             add-=r;
 95             p->len-=r;
 96             p->opp->len+=r;
 97         }
 98         p=p->to;
 99     }
100     return totr;
101 }
102 
103 void print(int x)
104 {
105     node *p=e[x];
106     while (p)
107     {
108         if (p->cond && p->len)
109         {
110             x=p->d;
111             if (x!=mid)
112                 print(x);
113             break;
114         }
115         p=p->to;
116     }
117     printf("%d ",x);
118 }
119 
120 int main()
121 {
122     node *p;
123     int T,n,m,x,y,i,s,t,sum;
124     scanf("%d",&T);
125     while (T--)
126     {
127         scanf("%d%d",&n,&m);
128         scanf("%d%d%d",&s,&t,&mid);
129         ss=n+1;
130         tt=n+2;
131         for (i=1;i<=n+2;i++)
132             e[i]=0;
133         addedge(n+1,mid,2);
134         addedge(s,n+2,1);
135         addedge(t,n+2,1);
136         while (m--)
137         {
138             scanf("%d%d",&x,&y);
139             addedge(x,y,1);
140             addedge(y,x,1);
141         }
142 
143         sum=0;
144         while (bfs())
145             sum+=dfs(ss,inf);
146 
147 //        assert(sum==2);
148 
149         ///有可能出现环结构 x->y->z->x or others, 去环
150         memset(pre,0,sizeof(pre));
151         ans_p=0;
152         x=s;
153         while (x!=mid)
154         {
155             pr[++ans_p]=x;
156             p=e[x];
157             while (p)
158             {
159                 if (p->cond && p->len && !p->visit)
160                 {
161                     x=p->d;
162                     p->visit=1;
163                     break;
164                 }
165                 p=p->to;
166             }
167             if (pre[x])
168                 ans_p=pre[x];
169             else
170                 pre[x]=ans_p+1;
171         }
172         for (i=1;i<=ans_p;i++)
173             printf("%d ",pr[i]);
174 
175         memset(pre,0,sizeof(pre));
176         ans_p=0;
177         x=t;
178         while (x!=mid)
179         {
180             pr[++ans_p]=x;
181             p=e[x];
182             while (p)
183             {
184                 if (p->cond && p->len && !p->visit)
185                 {
186                     x=p->d;
187                     p->visit=1;
188                     break;
189                 }
190                 p=p->to;
191             }
192             if (pre[x])
193                 ans_p=pre[x];
194             else
195                 pre[x]=ans_p+1;
196         }
197         printf("%d",mid);
198         for (i=ans_p;i>=1;i--)
199             printf(" %d",pr[i]);
200         printf("\n");
201 
202 //        ///100*99=9900 *10 sometimes need
203 //        node *pp;
204 //        for (i=1;i<=n+2;i++)
205 //        {
206 //            p=e[i];
207 //            while (p)
208 //            {
209 //                p->visit=0;
210 //                pp=p;
211 //                p=p->to;
212 //                free(pp);
213 //            }
214 //        }
215     }
216     return 0;
217 }
218 /*
219 5
220 
221 5 5
222 1 5 3
223 1 2
224 2 3
225 3 4
226 4 5
227 5 1
228 
229 5 5
230 1 3 5
231 1 2
232 2 3
233 3 4
234 4 5
235 5 1
236 
237 3 3
238 1 2 3
239 2 1
240 2 3
241 3 1
242 
243 4 6
244 2 1 4
245 1 2
246 1 3
247 1 4
248 2 3
249 2 4
250 3 4
251 
252 10 10
253 5 3 10
254 1 2
255 2 3
256 3 4
257 4 5
258 5 6
259 6 7
260 7 8
261 8 9
262 9 10
263 10 1
264 
265 
266 
267 3 0
268 1 2 3
269 
270 
271 1
272 5 6
273 2 1 4
274 1 2
275 2 4
276 4 5
277 4 3
278 5 1
279 3 1
280 */

错误代码2

费用流不拆点

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cstring>
  4 #include <string>
  5 #include <cmath>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10 #include <queue>
 11 const int maxn=1e2+10;
 12 const int inf=1e9;
 13 #include <assert.h>
 14 
 15 /*
 16 时间复杂度为O(N*E*k)，其中K为最大流值。但时间上的期望时间复杂度为：O(A*E*K)，其中A为所有顶点进队列的平均次数，可以证明A一般小于等于2。
 17 */
 18 
 19 struct node
 20 {
 21     int d,len,cost,cond;
 22     node *to,*opp;
 23 }*e[maxn],*pre[maxn];
 24 
 25 int ss,tt,dist[maxn],add[maxn],flow,fee;
 26 bool vis[maxn];
 27 int ans_p,pr[maxn];
 28 
 29 queue<int>st;
 30 
 31 void addedge(int x,int y,int len,int cost)
 32 {
 33     node *p1,*p2;
 34     p1=new node();
 35     p2=new node();
 36 
 37     p1->d=y;
 38     p1->len=len;
 39     p1->cost=cost;
 40     p1->opp=p2;
 41     p1->to=e[x];
 42     p1->cond=0;
 43     e[x]=p1;
 44 
 45     p2->d=x;
 46     p2->len=0;
 47     p2->cost=-cost;
 48     p2->opp=p1;
 49     p2->to=e[y];
 50     p2->cond=1;
 51     e[y]=p2;
 52 }
 53 
 54 void bfs()
 55 {
 56     node *p;
 57     int d,dd;
 58     while (1)
 59     {
 60         memset(dist,0x7f,sizeof(dist));
 61         dist[ss]=0;
 62         add[ss]=inf;
 63         add[tt]=0;
 64 
 65         st.push(ss);
 66         while (!st.empty())
 67         {
 68             d=st.front();
 69             st.pop();
 70             p=e[d];
 71             while (p)
 72             {
 73                 dd=p->d;
 74                 if (p->len && dist[dd]>dist[d]+p->cost)
 75                 {
 76                     dist[dd]=dist[d]+p->cost;
 77                     add[dd]=min(add[d],p->len);
 78                     pre[dd]=p->opp;
 79                     if (!vis[dd])
 80                     {
 81                         vis[dd]=1;
 82                         st.push(dd);
 83                     }
 84                 }
 85                 p=p->to;
 86             }
 87             vis[d]=0;
 88         }
 89 
 90         if (add[tt]==0)
 91             break;
 92 
 93         flow+=add[tt];
 94         fee+=add[tt]*dist[tt];
 95         d=tt;
 96         while (d!=ss)
 97         {
 98             pre[d]->len+=add[tt];
 99             pre[d]->opp->len-=add[tt];
100             d=pre[d]->d;
101         }
102     }
103 }
104 
105 int main()
106 {
107     node *p;
108     int T,n,m,x,y,i,mid,s,t;
109     scanf("%d",&T);
110     while (T--)
111     {
112         scanf("%d%d",&n,&m);
113         scanf("%d%d%d",&s,&t,&mid);
114         ss=n+1;
115         tt=n+2;
116         for (i=1;i<=n+2;i++)
117             e[i]=0;
118         addedge(n+1,mid,2,1);
119         addedge(s,n+2,1,1);
120         addedge(t,n+2,1,1);
121         while (m--)
122         {
123             scanf("%d%d",&x,&y);
124             if (x!=s && x!=t)
125                 addedge(x,y,1,1);
126             if (y!=s && y!=t)
127                 addedge(y,x,1,1);
128         }
129 
130         flow=0,fee=0;
131         bfs();
132 
133 //        printf("data=%d %d %d\n",s,t,mid);
134 
135         if (flow!=2)
136         {
137             printf("-1\n");
138             continue;
139         }
140 
141         ans_p=0;
142         x=s;
143         while (x!=mid)
144         {
145             pr[++ans_p]=x;
146             p=e[x];
147             while (p)
148             {
149                 if (p->cond && p->len)
150                 {
151                     x=p->d;
152                     break;
153                 }
154                 p=p->to;
155             }
156         }
157         for (i=1;i<=ans_p;i++)
158             printf("%d ",pr[i]);
159 
160         ans_p=0;
161         x=t;
162         while (x!=mid)
163         {
164             pr[++ans_p]=x;
165             p=e[x];
166             while (p)
167             {
168                 if (p->cond && p->len)
169                 {
170                     x=p->d;
171                     break;
172                 }
173                 p=p->to;
174             }
175         }
176         printf("%d",mid);
177         for (i=ans_p;i>=1;i--)
178             printf(" %d",pr[i]);
179         printf("\n");
180     }
181     return 0;
182 }
183 /*
184 5
185 
186 5 5
187 1 5 3
188 1 2
189 2 3
190 3 4
191 4 5
192 5 1
193 
194 5 5
195 1 3 5
196 1 2
197 2 3
198 3 4
199 4 5
200 5 1
201 
202 3 3
203 1 2 3
204 2 1
205 2 3
206 3 1
207 
208 4 6
209 2 1 4
210 1 2
211 1 3
212 1 4
213 2 3
214 2 4
215 3 4
216 
217 10 10
218 5 3 10
219 1 2
220 2 3
221 3 4
222 4 5
223 5 6
224 6 7
225 7 8
226 8 9
227 9 10
228 10 1
229 
230 3 0
231 1 2 3
232 
233 5 6
234 2 1 4
235 1 2
236 2 4
237 4 5
238 4 3
239 5 1
240 3 1
241 
242 */

构造时出现的困难：

1.费用流不能有负环从而无法设置更大的负值，从而决定一定要走哪条边

2.上下界可行流

想过设置mid->mid+n(可以再加上s->s+n和t->t+n)下界为1

但是无法做到流形成一条路径

如d->d+n下界为1，点d与点p相连，则可以为

sss->d+n->p->p+n->d->ttt

可以判断dfs形成的解是否为一条从s到t的链，

但是dfs形成的解太多，时间复杂度无法降下来。

由于无法解决这个问题，那么进一步的想法也没有意义了：

设置所有的点 d->d+n，使所有点从必须遍历，随机选择一个起点，终点为其中一个与起点相连的点，求网络流，解为哈密顿回路。

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <set>
  8 #include <map>
  9 #include <queue>
 10 #include <iostream>
 11 using namespace std;
 12 
 13 #define ll long long
 14 
 15 const int maxn=2e2+10;
 16 const int maxm=1e4;
 17 const int inf=1e9;
 18 const double eps=1e-8;
 19 
 20 struct node
 21 {
 22     int d,len,cond;
 23     node *to,*opp;
 24 }*e[maxn];
 25 
 26 int dif[maxn],dep[maxn],q[maxn],n,low[maxm],ss,tt,st,en;
 27 
 28 void addedge(int x,int y,int z)
 29 {
 30 //    printf("===%d %d %d\n",x,y,z);
 31 
 32     node *p1,*p2;
 33     p1=new node();
 34     p2=new node();
 35 
 36     p1->d=y;
 37     p1->len=z;
 38     p1->opp=p2;
 39     p1->to=e[x];
 40     e[x]=p1;
 41     p1->cond=0;
 42 
 43     p2->d=x;
 44     p2->len=0;
 45     p2->opp=p1;
 46     p2->to=e[y];
 47     e[y]=p2;
 48     p2->cond=1;
 49 }
 50 
 51 bool bfs()
 52 {
 53     node *p;
 54     int head=0,tail=1,d,dd;
 55     memset(dep,0,sizeof(dep));
 56     dep[st]=1;
 57     q[1]=st;
 58     while (head<tail)
 59     {
 60         head++;
 61         d=q[head];
 62         p=e[d];
 63         while (p)
 64         {
 65             dd=p->d;
 66             if (!dep[dd] && p->len)
 67             {
 68                 q[++tail]=dd;
 69                 dep[dd]=dep[d]+1;
 70             }
 71             p=p->to;
 72         }
 73     }
 74     if (dep[en])
 75         return 1;
 76     return 0;
 77 }
 78 
 79 int dfs(int d,int add)
 80 {
 81     if (!add || d==en)
 82         return add;
 83     int totr=0,r,dd;
 84     node *p=e[d];
 85     while (p)
 86     {
 87         dd=p->d;
 88         if (dep[dd]==dep[d]+1 && (r=dfs(dd,min(add,p->len)))>0)
 89         {
 90             totr+=r;
 91             add-=r;
 92             p->len-=r;
 93             p->opp->len+=r;
 94         }
 95         p=p->to;
 96     }
 97     return totr;
 98 }
 99 
100 int main()
101 {
102     node *p;
103     int T,n,m,x,y,i,mid,s,t,sum,sss,ttt;
104     scanf("%d",&T);
105     while (T--)
106     {
107         scanf("%d%d",&n,&m);
108         scanf("%d%d%d",&s,&t,&mid);
109 
110         for (i=1;i<=2*n+4;i++)
111             e[i]=0;
112         sss=2*n+3;
113         ttt=2*n+4;
114         ss=2*n+1;
115         tt=2*n+2;
116         addedge(ss,s,1);
117         addedge(t+n,tt,1);
118         for (i=1;i<=n;i++)
119             if (i==mid || i==s || i==t)
120                 addedge(i,i+n,1-1);
121             else
122                 addedge(i,i+n,1);
123 
124         addedge(sss,mid+n,1);///
125         addedge(mid,ttt,1);
126 
127         addedge(sss,s+n,1);///
128         addedge(s,ttt,1);
129 
130         addedge(sss,t+n,1);///
131         addedge(t,ttt,1);
132 
133         int tot=1;
134         while (m--)
135         {
136             scanf("%d%d",&x,&y);
137             addedge(x+n,y,1);
138             addedge(y+n,x,1);
139         }
140 
141         addedge(tt,ss,inf);
142 
143         st=sss,en=ttt;
144         sum=0;
145         while (bfs())
146             sum+=dfs(st,inf);
147 //        if (sum==tot)
148 //        {
149 //            sum=0;
150 //            st=ss,en=tt;
151 //            while (bfs())
152 //                sum+=dfs(st,inf);
153 
154             x=s;
155             while (x!=mid)
156             {
157                 if (x<=n)
158                     printf("%d ",x);
159                 p=e[x];
160                 while (p)
161                 {
162                     if (!p->cond && p->opp->len)
163                         break;
164                     p=p->to;
165                 }
166             }
167             ///
168             x=mid+n;
169             while (x!=t)
170             {
171                 if (x<=n)
172                     printf("%d ",x);
173                 p=e[x];
174                 while (p)
175                 {
176                     if (!p->cond && p->opp->len)
177                         break;
178                     p=p->to;
179                 }
180             }
181             printf("%d\n",t);
182 
183 //        }
184 //        else
185 //            printf("please go home to sleep");
186     }
187     return 0;
188 }
189 /*
190 4 3 1 4
191 2 3 2 3
192 1 2 0 100
193 3 4 0 100
194 
195 4 3 1 4
196 2 3 0 3
197 1 2 0 100
198 3 4 0 100
199 */

造数据：

 1 #include <cstdio>
 2 #include <cstdlib>
 3 #include <cstring>
 4 #include <string>
 5 #include <cmath>
 6 #include <algorithm>
 7 #include <iostream>
 8 using namespace std;
 9 #define ll long long
10 #include <time.h>
11 
12 const int maxn=1e2+10;
13 
14 bool vis[maxn][maxn];
15 int px[maxn*maxn],py[maxn*maxn];
16 
17 int main()
18 {
19     int t,n,m,x,y,z,i;
20     srand(time(NULL));
21     FILE *in=fopen("1.in","w");
22     t=1000;
23     fprintf(in,"%d\n",t);
24     while (t--)
25     {
26         do
27         {
28             n=rand()%100+1;
29         }
30         while (n<=2);
31         m=rand()%(n*(n-1)/2)+1;
32 
33         x=rand()%n+1;
34         do
35             y=rand()%n+1;
36         while (y==x);
37         do
38             z=rand()%n+1;
39         while (z==x || z==y);
40 
41         fprintf(in,"%d %d\n",n,m);
42         fprintf(in,"%d %d %d\n",x,y,z);
43 
44 
45         memset(vis,0,sizeof(vis));
46         for (i=1;i<=m;)
47         {
48             x=rand()%n+1;
49             do
50                 y=rand()%n+1;
51             while (y==x);
52             if (!vis[x][y])
53             {
54                 px[i]=x,py[i]=y;
55                 i++;
56             }
57         }
58         for (i=1;i<=m;i++)
59             fprintf(in,"%d %d\n",px[i],py[i]);
60         fprintf(in,"\n");
61     }
62     fclose(in);
63     return 0;
64 }

练习题：

P2045 方格取数加强版

https://www.luogu.org/problemnew/show/P2045

获得最大值需要的最少部分(自己造的！)

网络流+二分

posted @ 2019-06-19 18:27 congmingyige 阅读(193) 评论(0) 编辑收藏举报

刷新页面返回顶部

congmingyige

网络流进阶

公告