Minieye杯第十五届华中科技大学程序设计邀请赛现场同步赛

良心的题目和解法，quite bad的题面和题解。。。

AMatrix

原题。。。

from https://codeforces.com/problemset/problem/811/E

E. Vladik and Entertaining Flags

线段树+并查集

见代码注释

时间复杂度：

在正常线段树的基础上，

每两列的合并O(n)，常数较大

build：总共合并n次，O(n^2)

query：

如最坏情况

n=2^k

1~n-1

需要合并判断

1~n/2 与 n/2+1~n/2

n/2+1~n/4*3 与 n/4*3+1~n

……

共k次，可认为是log(n)次

q次询问，O(q * log(n)*n)

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10 
 11 const double eps=1e-8;
 12 const ll inf=1e9;
 13 const ll mod=1e9+7;
 14 const int maxn=1e5+10;
 15 const int maxm=10;
 16 
 17 /**
 18 两个小区间合并成一个小区间：
 19 左区间最右边的一列 右区间最左边的一列 combined using 并查集
 20 
 21 一个区间的数目为:
 22 两个小区间的数目之和 - 两个小区间交界部分相同的数目
 23 **/
 24 
 25 struct node
 26 {
 27     ///左区间最右边的一列 右区间最左边的一列 连通块数目
 28     int left[maxm],right[maxm],cnt;
 29 }f[maxn<<2];
 30 
 31 int n,m,id;
 32 int a[maxn][10],fa[maxn*10],tl[maxm],tr[maxm];
 33 
 34 int getf(int d)
 35 {
 36     if (fa[d]==d)
 37         return d;
 38     fa[d]=getf(fa[d]);
 39     return fa[d];
 40 }
 41 
 42 ///从小到大，处理[区间1_left,区间2_right]，保证区间1和区间2已经处理完毕
 43 void merge_interval(node &x,node &y,node &z,int pos)
 44 {
 45     int i,cnt=0;
 46     memcpy(tl,y.right,n*4);///
 47     memcpy(tr,z.left,n*4);///
 48     ///must
 49     ///不修改之前的数值
 50     for (i=0;i<n;i++)
 51     {
 52         fa[tl[i]]=tl[i];
 53         fa[tr[i]]=tr[i];
 54         fa[y.left[i]]=y.left[i];///
 55         fa[z.right[i]]=z.right[i];///
 56     }
 57     for (i=0;i<n;i++)
 58         if (a[pos][i]==a[pos+1][i])
 59         {
 60             tl[i]=getf(tl[i]);
 61             tr[i]=getf(tr[i]);
 62             if (tl[i]!=tr[i])
 63             {
 64                 fa[tl[i]]=tr[i];
 65                 cnt++;
 66             }
 67             /**
 68             在之前还没被合并，见例子
 69             1 1 1 yes
 70             1 2 1
 71             1 1 1 no
 72             **/
 73         }
 74 
 75     x.cnt=y.cnt+z.cnt-cnt;
 76     ///经过两列合并的修改(左边/右边列的哪些原来不属于同一个集合的两个数，经过合并后，属于同一个集合)
 77     for (i=0;i<n;i++)
 78     {
 79         x.left[i]=getf(y.left[i]);
 80         x.right[i]=getf(z.right[i]);
 81     }
 82 }
 83 
 84 void build(int ind,int l,int r)
 85 {
 86     if (l==r)
 87     {
 88         ///一列中连续的数字的父亲相同即可
 89         int cnt=0,i;
 90         for (i=0;i<n;i++)
 91         {
 92             if (i==0 || a[l][i]!=a[l][i-1])
 93                 id++,cnt++;
 94             f[ind].left[i]=f[ind].right[i]=id;
 95         }
 96         f[ind].cnt=cnt;
 97         return ;
 98     }
 99 
100     int m=(l+r)>>1;
101     build(ind<<1,l,m);
102     build(ind<<1|1,m+1,r);
103 
104     merge_interval(f[ind],f[ind<<1],f[ind<<1|1],m);
105 }
106 
107 node query(int ind,int l,int r,int x,int y)
108 {
109     if (x<=l && r<=y)
110         return f[ind];
111     int m=(l+r)>>1;
112     node u,v,w;
113     if (x<=m)
114         u=query(ind<<1,l,m,x,y);
115     if (m<y)
116         v=query(ind<<1|1,m+1,r,x,y);
117     ///不改变f[ind<<1]和f[ind<<1|1]的值
118 
119     if (x<=m && m<y)
120     {
121         merge_interval(w,u,v,m);
122         return w;
123     }
124     else if (x<=m)
125         return u;
126     else
127         return v;
128 }
129 
130 int main()
131 {
132     int Q,i,j;
133     scanf("%d%d%d",&n,&m,&Q);
134     for (i=0;i<n;i++)
135         for (j=0;j<m;j++)
136             scanf("%d",&a[j][i]);
137 
138     build(1,0,m-1);
139 
140     while (Q--)
141     {
142         scanf("%d%d",&i,&j);
143         i--,j--;
144         printf("%d\n",query(1,0,m-1,i,j).cnt);
145     }
146 
147     return 0;
148 }
149 /*
150 x 1 y
151 
152 
153 3 3 4
154 1 1 1
155 1 2 1
156 1 1 1
157 1 3
158 wrong
159 1 =1
160 1->2 0
161 2->3 -1
162 实际上，第二列的两个数，在第一列中
163 
164 5 3 4
165 1 1 1
166 1 2 1
167 1 1 1
168 1 2 1
169 1 1 1
170 2 3
171 1 2
172 1 3
173 
174 4 5 10
175 1 1 2 1 1
176 2 1 2 3 1
177 1 1 1 2 1
178 2 4 1 1 1
179 2 4
180 2 5
181 1 4
182 1 5
183 
184 1 15 10
185 1 1 1 1 2 1 2 2 3 2 2 1 1 1 10000
186 1 15
187 2 6
188 3 10
189 4 8
190 
191 4 10 10
192 7 9 4 3 1 9 4 7 1 7
193 1 3 8 7 8 5 7 9 1 7
194 7 2 2 3 7 7 1 6 5 9
195 6 7 9 4 2 5 8 5 7 2
196 2 6
197 
198 */

其它类似题目：

hdu6392 Reverse Game

可持久化（https://www.luogu.org/problem/P3402）

[WC2005]双面棋盘
https://www.luogu.org/problem/P4121

-------------------------

我之前错误的方法

k列->k+1列的变化

cal(k,k+1)-cal(k,k)

x~y: 第x列 + k列->k+1列 + k+1列->k+2列 -> y-1列->y列

线段树

无法用于

3 3 4
1 1 1
1 2 1
1 1 1
1 3

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10  
 11 const double eps=1e-8;
 12 const ll inf=1e9;
 13 const ll mod=1e9+7;
 14 const int maxn=1e5+10;
 15  
 16 /**
 17 try to save memory as much as possible
 18 **/
 19  
 20 int a[10][maxn],n,m,qx[maxn*10],qy[maxn*10];
 21  
 22 int f[maxn<<2],g[maxn],z[maxn];
 23 bool vis[10][maxn];
 24  
 25 int dx[4]={-1,0,0,1};
 26 int dy[4]={0,-1,1,0};
 27  
 28 int cal(int yl,int yr)
 29 {
 30     int cnt=0,i,j,k,head,tail,x,y,xx,yy;
 31     for (i=0;i<=n-1;i++)
 32         for (j=yl;j<=yr;j++)
 33             vis[i][j]=0;
 34     for (i=0;i<=n-1;i++)
 35         for (j=yl;j<=yr;j++)
 36             if (!vis[i][j])
 37             {
 38                 head=0,tail=1;
 39                 qx[1]=i,qy[1]=j;
 40                 while (head<tail)
 41                 {
 42                     head++;
 43                     x=qx[head];
 44                     y=qy[head];
 45                     for (k=0;k<4;k++)
 46                     {
 47                         xx=x+dx[k];
 48                         yy=y+dy[k];
 49                         if (xx>=0 && xx<=n-1 && yy>=yl && yy<=yr && !vis[xx][yy] && a[x][y]==a[xx][yy])
 50                         {
 51                             qx[++tail]=xx;
 52                             qy[tail]=yy;
 53                             vis[xx][yy]=1;
 54                         }
 55                     }
 56                 }
 57                 cnt++;
 58             }
 59     return cnt;
 60 }
 61  
 62 void build(int ind,int l,int r)
 63 {
 64     if (l==r)
 65         z[ind]=f[l];
 66     else
 67     {
 68         int m=(l+r)>>1;
 69         build(ind<<1,l,m);
 70         build(ind<<1|1,m+1,r);
 71         z[ind]=z[ind<<1]+z[ind<<1|1];
 72     }
 73 }
 74  
 75 int query(int ind,int l,int r,int x,int y)
 76 {
 77     if (x<=l && r<=y)
 78         return z[ind];
 79     int m=(l+r)>>1,sum=0;
 80     if (x<=m)
 81         sum+=query(ind<<1,l,m,x,y);
 82     if (m<y)
 83         sum+=query(ind<<1|1,m+1,r,x,y);
 84     return sum;
 85 }
 86  
 87 int main()
 88 {
 89     int Q,i,j;
 90     scanf("%d%d%d",&n,&m,&Q);
 91     for (j=0;j<n;j++)
 92         for (i=0;i<m;i++)
 93             scanf("%d",&a[j][i]);
 94  
 95     ///pth -> (p+1)th the number of blocks changes f[l][p+1]
 96 //            printf("l=%d\n",l);
 97     for (i=0;i<m;i++)
 98         g[i]=cal(i,i);    ///can also calculate when querying
 99     for (i=1;i<m;i++)
100         f[i]=cal(i-1,i)-g[i-1];
101  
102     build(1,0,m-1);
103  
104     while (Q--)
105     {
106         scanf("%d%d",&i,&j);
107         i--,j--;
108         printf("%d\n",(i==j?0:query(1,0,m-1,i+1,j)) + g[i]);   ///注意优先级，一定要加括号
109     }
110  
111     return 0;
112 }
113 /*
114 10 1 10
115 1
116 2
117 1
118 1
119 1
120 1
121 2
122 1
123 3
124 1
125 */

错误代码

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10  
 11 const double eps=1e-8;
 12 const ll inf=1e9;
 13 const ll mod=1e9+7;
 14 const int maxn=1e5+10;
 15  
 16 /**
 17 try to save memory as much as possible
 18 **/
 19  
 20 int a[10][maxn],n,m,qx[maxn*10],qy[maxn*10];
 21  
 22 int f[maxn<<2],g[maxn],z[maxn];
 23 bool vis[10][maxn];
 24  
 25 int dx[4]={-1,0,0,1};
 26 int dy[4]={0,-1,1,0};
 27  
 28 int cal(int yl,int yr)
 29 {
 30     int cnt=0,i,j,k,head,tail,x,y,xx,yy;
 31     for (i=0;i<=n-1;i++)
 32         for (j=yl;j<=yr;j++)
 33             vis[i][j]=0;
 34     for (i=0;i<=n-1;i++)
 35         for (j=yl;j<=yr;j++)
 36             if (!vis[i][j])
 37             {
 38                 head=0,tail=1;
 39                 qx[1]=i,qy[1]=j;
 40                 while (head<tail)
 41                 {
 42                     head++;
 43                     x=qx[head];
 44                     y=qy[head];
 45                     for (k=0;k<4;k++)
 46                     {
 47                         xx=x+dx[k];
 48                         yy=y+dy[k];
 49                         if (xx>=0 && xx<=n-1 && yy>=yl && yy<=yr && !vis[xx][yy] && a[x][y]==a[xx][yy])
 50                         {
 51                             qx[++tail]=xx;
 52                             qy[tail]=yy;
 53                             vis[xx][yy]=1;
 54                         }
 55                     }
 56                 }
 57                 cnt++;
 58             }
 59     return cnt;
 60 }
 61  
 62 void build(int ind,int l,int r)
 63 {
 64     if (l==r)
 65         z[ind]=f[l];
 66     else
 67     {
 68         int m=(l+r)>>1;
 69         build(ind<<1,l,m);
 70         build(ind<<1|1,m+1,r);
 71         z[ind]=z[ind<<1]+z[ind<<1|1];
 72     }
 73 }
 74  
 75 int query(int ind,int l,int r,int x,int y)
 76 {
 77     if (x<=l && r<=y)
 78         return z[ind];
 79     int m=(l+r)>>1,sum=0;
 80     if (x<=m)
 81         sum+=query(ind<<1,l,m,x,y);
 82     if (m<y)
 83         sum+=query(ind<<1|1,m+1,r,x,y);
 84     return sum;
 85 }
 86  
 87 int main()
 88 {
 89     int Q,i,j;
 90     scanf("%d%d%d",&n,&m,&Q);
 91     for (j=0;j<n;j++)
 92         for (i=0;i<m;i++)
 93             scanf("%d",&a[j][i]);
 94  
 95     ///pth -> (p+1)th the number of blocks changes f[l][p+1]
 96 //            printf("l=%d\n",l);
 97     for (i=0;i<m;i++)
 98         g[i]=cal(i,i);    ///can also calculate when querying
 99     for (i=1;i<m;i++)
100         f[i]=cal(i-1,i)-g[i-1];
101  
102     build(1,0,m-1);
103  
104     while (Q--)
105     {
106         scanf("%d%d",&i,&j);
107         i--,j--;
108         printf("%d\n",(i==j?0:query(1,0,m-1,i+1,j)) + g[i]);   ///注意优先级，一定要加括号
109     }
110  
111     return 0;
112 }
113 /*
114 10 1 10
115 1
116 2
117 1
118 1
119 1
120 1
121 2
122 1
123 3
124 1
125 */

BMistake

树上差分

之后补题

CMassive

每个区间都有它的作用域

按照起始位置对区间进行排序

meet in begin point +1

meet in end point -1

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <set>
  7 #include <map>
  8 #include <list>
  9 #include <queue>
 10 #include <vector>
 11 #include <bitset>
 12 #include <algorithm>
 13 #include <iostream>
 14 using namespace std;
 15 #define ll long long
 16  
 17 const double eps=1e-8;
 18 const ll inf=1e18;
 19 const int maxn=1e6+10;
 20  
 21 ///主席树可做 1~i的所有前缀和建线段树(i=1,2,...,n)
 22  
 23 int num[maxn],f[maxn];
 24 ll pf[maxn],b[maxn];
 25  
 26 struct node
 27 {
 28     ll x;
 29     int ind;
 30     bool operator<(const node &y) const
 31     {
 32         return x<y.x;
 33     }
 34 }a[maxn];
 35  
 36 ll cal(int j)
 37 {
 38     ll sum=0;
 39     while (j>=1)
 40     {
 41         sum+=f[j];
 42         j-=j&-j;
 43     }
 44     return sum;
 45 }
 46  
 47 int main()
 48 {
 49     int n,l,r,m,i,j;
 50     ll *k;
 51     ll s,x,sum=0,v;
 52     cin>>n>>l>>r>>s;
 53 //    scanf("%d%d%d%lld",&n,&l,&r,&s);
 54     for (i=1;i<=n;i++)
 55     {
 56 //        scanf("%lld",&x);
 57         cin>>x;
 58         pf[i]=pf[i-1]+x;
 59         a[i].x=pf[i];
 60         a[i].ind=i;
 61     }
 62     sort(a+1,a+n+1);
 63     a[0].x=a[1].x-1;
 64     m=0;
 65     for (i=1;i<=n;i++)
 66     {
 67         if (a[i].x!=a[i-1].x)
 68         {
 69             m++;
 70             b[m]=a[i].x;
 71         }
 72         num[a[i].ind]=m;
 73     }
 74  
 75     for (i=1;i<=n;i++)
 76     {
 77         j=num[i];
 78         while (j<=m)
 79         {
 80             f[j]++;
 81             j+=j&-j;
 82         }
 83  
 84  
 85         if (i>=l-1 && i<=n-1)
 86         {
 87             v=pf[i-l+1]+s;
 88             k=lower_bound(b+1,b+m+1,v);
 89             sum-=i-cal(k-b-1);
 90         }
 91  
 92         if (i>=r)
 93         {
 94             j=i-r+l-1;
 95             v=pf[i-r]+s;
 96             k=lower_bound(b+1,b+m+1,v);
 97             sum+=i-cal(k-b-1);
 98         }
 99     }
100  
101     for (i=n-r+1+1;i<=n-l+1;i++)
102     {
103         v=pf[i-1]+s;
104         k=lower_bound(b+1,b+m+1,v);
105         sum+=n-cal(k-b-1);
106     }
107  
108     printf("%lld",sum);
109     return 0;
110 }
111 /*
112 5 2 3 -100
113 1 2 -3 4 5
114  
115 5 1 1 1
116 1 2 -3 4 5
117  
118 1 1 1 1
119 2
120  
121 3 3 3 0
122 1 -1 2
123  
124 3 2 2 0
125 1 -1 2
126  
127 3 2 3 0
128 1 -1 2
129  
130 3 2 3 1
131 1 -1 2
132 */

DModule

学习了！

dp式子

系数固定，可使用快速幂

状态矩阵满足规律，可降低时间复杂度

然而数据的精度很xxx(哗啦哗啦)。

矩阵特性：一行的数值为上一行的数值平移一个单位得到，且不会随运算改变。所以只用记录一行的状态。所以矩阵相乘时，只需要得到一行的结果，即O(n^2)。

矩阵乘法操作

a^k * a^k =a^(2k)

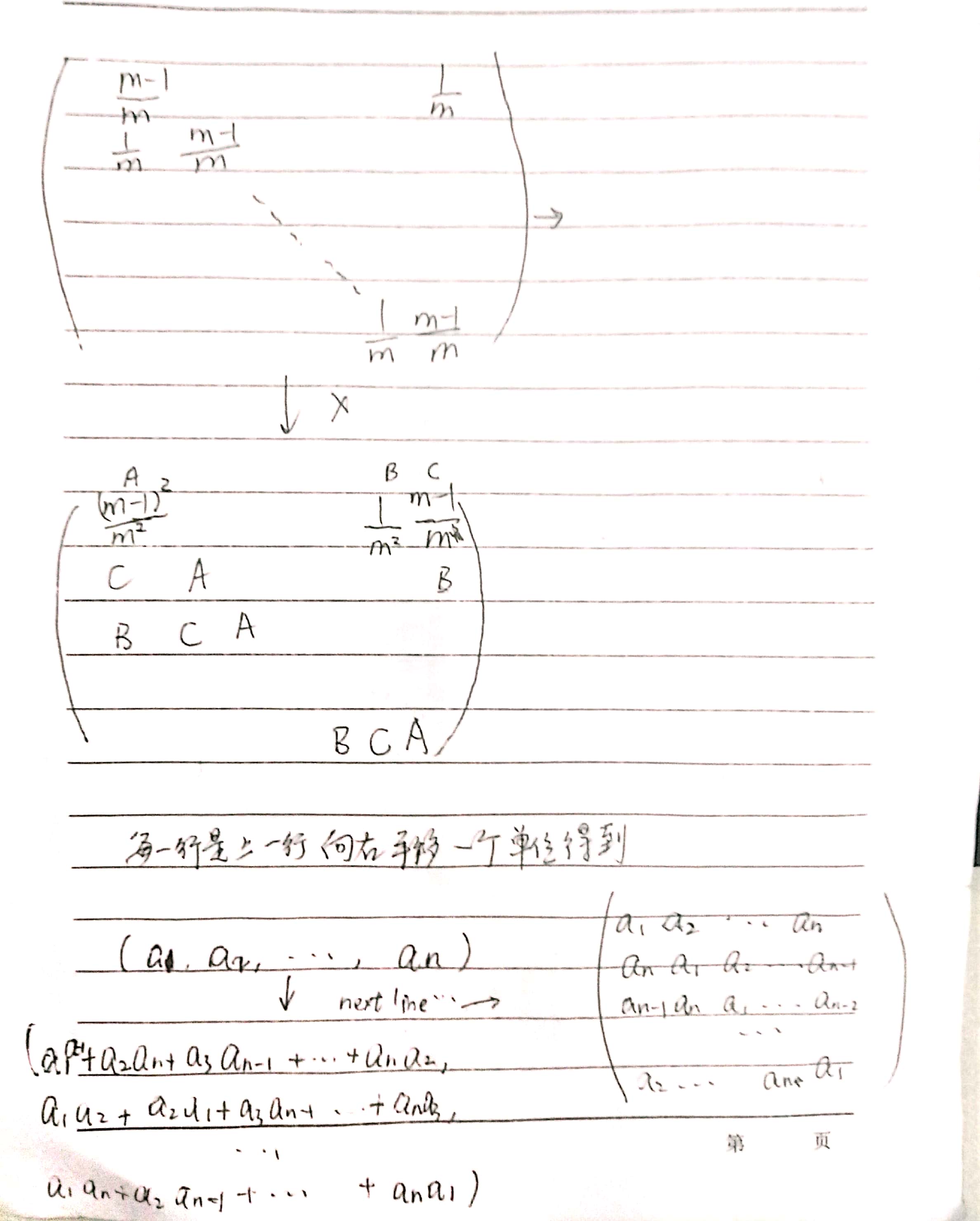
  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10  
 11 const double eps=1e-8;
 12 const ll inf=1e9;
 13 const ll mod=1e9+7;
 14 const int maxn=1e3+10;
 15  
 16 /**
 17 题目精度设得特别不好
 18 用long double,只能33.3%过
 19 用同样正确的方法(矩阵其它写法)，也是没过
 20  
 21  
 22 每个数都选一遍，最后除以m
 23 [ f[i-1][j-1]+(f[i-1][j]*m-f[i-1][j]) ]/m
 24  
 25 -f[i-1][j] 数j各有一次被选中
 26  
 27 **/
 28  
 29 double a[maxn];
 30 int n;
 31  
 32 struct mat
 33 {
 34     double a[maxn];
 35     mat()
 36     {
 37         memset(a,0,sizeof(a));   ///一定要，不知道为什么
 38     }
 39     void init()
 40     {
 41         a[0]=1;
 42     }
 43     mat operator*(const mat &y) const
 44     {
 45         mat z;
 46         for (int i=0;i<n;i++)
 47             for (int j=0;j<n;j++)
 48                 z.a[(i+j)%n]+=a[i]*y.a[j];
 49         return z;
 50     }
 51 };
 52  
 53 mat mul(mat a,ll b)
 54 {
 55     mat y;
 56     y.init();
 57     while (b)
 58     {
 59         if (b&1)
 60             y=y*a;
 61         a=a*a;
 62         b>>=1;
 63     }
 64     return y;
 65 }
 66  
 67 int main()
 68 {
 69 //    FILE *in=fopen("data.in","r");
 70 //    FILE *out=fopen("data.out","w");
 71     ll m,k,i,j;
 72     mat ori,y;
 73     double tot;
 74 //    fscanf(in,"%lld%lld%lld",&n,&m,&k);
 75     scanf("%lld%lld%lld",&n,&m,&k);
 76     for (i=0;i<n;i++)
 77 //        fscanf(in,"%lf",&a[i]);
 78         scanf("%lf",&a[i]);
 79  
 80 //    ori.a[0]=1-1.0/m;
 81 //    ori.a[n-1]=1.0/m;
 82  
 83     ori.a[0]=1.0-1.0/m;
 84     ori.a[1]=1.0/m;
 85  
 86     y=mul(ori,k);
 87  
 88     for (i=0;i<n;i++)
 89     {
 90         tot=0;
 91         for (j=0;j<n;j++)
 92             tot+=y.a[j]*a[(i-j+n)%n];
 93 //            tot+=y.a[(j-i+n)%n]*a[j];
 94 //        fprintf(out,"%.1f%c",tot,i==n-1?'\n':' ');
 95         printf("%.1f%c",tot,i==n-1?'\n':' ');
 96     }
 97 //    fclose(in);
 98 //    fclose(out);
 99     return 0;
100 }
101 /*
102 2 3 1
103 3 0
104 */

EManhattan

裸的bfs+二分答案

二分实现次数 log(M) 大约为10

一个更直观的方法是

求每个A点能否访问所有B点，赋予属性 [n^2]

然后求A点之间互相访问的情况，

一个集合，互相访问，则至少集合中有一个点，能访问所有的B点。 [N]

题解用并查集，也行。

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10 
 11 const double eps=1e-8;
 12 const ll inf=1e9;
 13 const ll mod=1e9+7;
 14 const int maxn=2e3+10;
 15 
 16 struct node
 17 {
 18     int x,y;
 19 }a[maxn];
 20 
 21 bool vis[maxn];
 22 int q[maxn],dist[maxn][maxn],use[maxn];
 23 
 24 int main()
 25 {
 26     int n,m,g,i,j,k,l,r,mid,sum1,sum2,head,tail,d;
 27     scanf("%d%d",&n,&m);
 28     for (i=1;i<=n;i++)
 29         scanf("%d%d",&a[i].x,&a[i].y);
 30     for (i=1;i<=m;i++)
 31         scanf("%d%d",&a[n+i].x,&a[n+i].y);
 32 
 33     ///can decrease
 34     int tp=n+m;
 35     for (i=1;i<=tp;i++)
 36         for (j=1;j<=tp;j++)
 37             dist[i][j]=abs(a[i].x-a[j].x) + abs(a[i].y-a[j].y);
 38 
 39     l=0,r=4000;///
 40     while (l<=r)
 41     {
 42         mid=(l+r)>>1;
 43 
 44         g=0;
 45         memset(use,0,sizeof(use));
 46         for (i=1;i<=n;i++)
 47             if (!use[i])
 48             {
 49                 memset(vis,0,sizeof(vis));
 50                 use[i]=1;
 51                 q[1]=i;
 52                 head=0,tail=1;
 53                 while (head<tail)
 54                 {
 55                     head++;
 56                     d=q[head];
 57                     for (j=1;j<=n;j++)
 58                         if (!use[j] && !vis[j] && dist[j][d]<=mid)
 59                         {
 60                             use[j]=1;
 61                             q[++tail]=j;
 62                         }
 63 
 64                     for (j=n+1;j<=tp;j++)
 65                         if (!vis[j] && dist[j][d]<=mid)
 66                             vis[j]=1,g++;
 67                 }
 68 
 69                 if (g!=m)
 70                     break;
 71             }
 72 
 73         if (i==n+1)
 74             r=mid-1;
 75         else
 76             l=mid+1;
 77     }
 78     sum1=l;
 79 
 80 
 81     mid=sum1+1;
 82 
 83     g=0;
 84     memset(use,0,sizeof(use));
 85     for (i=n+1;i<=tp;i++)
 86         if (!use[i])
 87         {
 88             memset(vis,0,sizeof(vis));
 89             use[i]=1;
 90             q[1]=i;
 91             head=0,tail=1;
 92             while (head<tail)
 93             {
 94                 head++;
 95                 d=q[head];
 96                 for (j=n+1;j<=tp;j++)
 97                     if (!use[j] && !vis[j] && dist[j][d]<=mid)
 98                     {
 99                         use[j]=1;
100                         q[++tail]=j;
101                     }
102 
103                 for (j=1;j<=n;j++)
104                     if (!vis[j] && dist[j][d]<=mid)
105                         vis[j]=1,g++;
106             }
107 
108             if (g!=n)
109                 break;
110         }
111 
112 
113     if (i!=tp+1)
114         printf("1");
115     else
116         printf("0");
117     return 0;
118 }
119 /*
120 1 1
121 2 3
122 4 5
123 
124 2 1
125 0 0
126 2 0
127 3 0
128 
129 2 1
130 0 0
131 2 0
132 4 0
133 */

FMesh

easy&funny problem

“对一个问题设置解决方案” 类题目

 1 #include <cstdio>
 2 #include <cstdlib>
 3 #include <cmath>
 4 #include <cstring>
 5 #include <string>
 6 #include <algorithm>
 7 #include <iostream>
 8 using namespace std;
 9 #define ll long long
10  
11 const double eps=1e-8;
12 const ll inf=1e9;
13 const ll mod=1e9+7;
14 const int maxn=5e5+10;
15  
16 /*
17 add 3*3 is also ok
18 so 2*3,3*2,3*3 在场上最多出现一次
19 设置之前矩阵的放置位置，使可以放置而不重叠，然后进行消除
20 */
21  
22 char str[maxn];
23  
24 int cond[4];
25  
26 int f[8][2]={
27 4,1,
28 4,4,
29 5,1,
30 5,4,
31 1,5,
32 4,5,
33 1,4,
34 4,4
35 };
36  
37 int main()
38 {
39     int n,i,j,k;
40     scanf("%s",str);
41     n=strlen(str);
42     for (i=0;i<n;i++)
43     {
44         j=str[i]-48;
45         k=(j<<1)|cond[j];
46         printf("%d %d\n",f[k][0],f[k][1]);
47         cond[j]^=1;
48     }
49     return 0;
50 }

GMath

看求解过程

1.dp

(不太清楚理解正不正确)

A.系数是确定的

多项式(N<=30)^M(N<=1e9)

多项式快速幂 log(NlogN)

多项式乘积的结果与初始矩阵相乘
多项式乘法 FFT log(NlogN)

---------------

dp优化

目标是使得sin(kx)变为若干个sin(yi)的运算，其中yi<kx。

at last

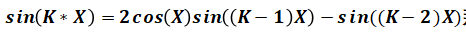(from PPT solution)

sin(k1*x)*sin(k2*X)*..*...*sin(km-1*X)*sin((K-1)X) : tot=N-1

sin(k1*x)*sin(k2*X)*..*...*sin(km-1*X)*sin((K-2)X) : tot=N-2

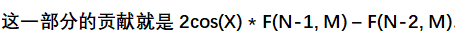(from PPT solution)

N-1 -> N 系数固定，可用快速幂

(2M)^3 * log(N) * T

1.结构体数组 must initialize for mat z(variable is not a constant)

2.快速幂可写在main函数里，初始的y，可赋值

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10 
 11 const double eps=1e-12;
 12 const ll inf=1e9;
 13 const ll mod=1e9+7;
 14 const int maxn=1e5+10;
 15 const int maxm=60+10;
 16 
 17 int mm;
 18 double v[maxm];
 19 
 20 struct mat
 21 {
 22     double a[maxm][maxm];
 23     mat()
 24     {
 25         memset(a,0,sizeof(a));  ///must initialize for mat z(variable is not a constant)
 26     }
 27     void init()
 28     {
 29         int i;
 30         memset(a,0,sizeof(a));
 31         for (i=1;i<=mm;i++)
 32             a[i][i]=1;
 33     }
 34     mat operator*(const mat &y) const
 35     {
 36         mat z;
 37         int i,j,k;
 38         for (k=1;k<=mm;k++)
 39             for (i=1;i<=mm;i++)
 40                 for (j=1;j<=mm;j++)
 41                     z.a[i][j]+=a[i][k]*y.a[k][j];
 42         return z;
 43     }
 44 }mat0,mat1;
 45 
 46 mat mul(mat a,int b)
 47 {
 48     mat y;
 49     y.init();
 50     while (b)
 51     {
 52         if (b&1)
 53             y=y*a;
 54         a=a*a;
 55         b>>=1;
 56     }
 57     return y;
 58 }
 59 
 60 
 61 int main()
 62 {
 63     int t,m,M,n,i,j;
 64     double x,tot;
 65     mat mat0,mat1;
 66     scanf("%d",&t);
 67     m=30,mm=60;
 68     while (t--)
 69     {
 70         scanf("%d%d%lf",&M,&n,&x);
 71 //        mm=m<<1;
 72         ///写成30,60:避免覆盖 当n=1,2时 (v[1],v[2],v[m+1])
 73         ///i=1..m F[N-1][i] ; j=(i=1..n)+m F[N-2][i]
 74         ///F[N]
 75         memset(mat0.a,0,sizeof(mat0.a));
 76         for (i=1;i<=m;i++)
 77         {
 78             mat0.a[i][i]=cos(x)*2;
 79             mat0.a[i][i+m]=-1;
 80             ///注意 mat0.a[p][q] * v[q] [...][p]使用[...][q]
 81             if (i!=1)
 82                 mat0.a[i][i-1]=sin(x);
 83         }
 84         ///F[N-1]
 85         for (i=m+1;i<=mm;i++)
 86             mat0.a[i][i-m]=1;
 87         ///F[2]
 88         memset(v,0,sizeof(v));
 89         v[1]=sin(x*2);
 90         v[2]=sin(x)*sin(x);
 91         ///F[1]
 92         v[m+1]=sin(x);
 93 //        v[1]=sin(x);
 94 //        for (i=1;i<=m;i++)
 95 //            v[i]=i;
 96 //        ///F[0]
 97 //        for (i=m+1;i<=mm;i++)
 98 //            v[i]=0;
 99 
100         ///F[n+1] F[n]
101         mat1=mul(mat0,n-1);
102 //        mat1=mul(mat0,n);
103         tot=0;
104         ///F[n] right part
105         for (j=1;j<=mm;j++)
106             tot+=mat1.a[m+M][j]*v[j];
107 
108         ///另外的写法：初始的矩阵y(in mul function)=v，快速幂直接在main函数内写
109 
110         if (!(fabs(tot)>eps && tot<0))
111             printf("+");
112         else
113         {
114             printf("-");
115             tot=-tot;
116         }
117         while (tot<1)
118             tot*=10;
119         while (tot>=10)
120             tot/=10;
121         printf("%d\n",(int)tot);
122     }
123     return 0;
124 }
125 /*
126 4
127 1 1 1
128 2 2 1
129 3 3 1
130 4 4 1
131 sin(1)=0.84147
132 ‭0.8414709848078965066525023216303‬
133 ‭0.70807341827357119349878411475038‬
134 ‭0.595821144644523‬
135 ‭0.50136796566561970416888809186316‬
136 
137 2
138 1 0 1
139 2 0 1
140 */

HModify

一个点能到达的点中最小的属性

tarjan[每个互相能访问的集合]+缩点[一个集合能访问另外哪些集合，无环]

建树给每个字符串赋予编号 or 使用hash

然后方法有点绕了。

-------------------------

题解的方法：

反边，排序。

修改的代价从小到大，该方案能到达的所有字符串(还没被处理)选择该方案（也就是当前代价最小的方案）。

学习了！

代码1

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10  
 11 const double eps=1e-8;
 12 const ll inf=1e9;
 13 const ll mod=1e9+7;
 14 const int maxn=3e5+10;
 15 const int maxm=5e5+10;
 16  
 17 struct node
 18 {
 19     int d;
 20     node *to;
 21 }*e[maxn];
 22  
 23 struct rec
 24 {
 25     int num;
 26     rec *nex[26];
 27 }*tr;
 28  
 29 struct word
 30 {
 31     ll x,y;
 32 }value[maxn],va,group_value[maxn];
 33  
 34 int num,ind,low[maxn],dfn[maxn],st[maxn],cnt_st,cnt_group,group[maxn],b[maxn];
 35 bool vis[maxn],vis_st[maxn];
 36  
 37 char str[maxm];
 38  
 39 word min(word a,word b)
 40 {
 41     if (a.x==b.x)
 42         return a.y<b.y?a:b;
 43     return a.x<b.x?a:b;
 44 }
 45  
 46 int build()
 47 {
 48     rec *pos,*p;
 49     int len,d,i,x=0;
 50     scanf("%s",str);
 51     len=strlen(str);
 52  
 53     pos=tr;
 54     for (i=0;i<len;i++)
 55     {
 56         d=str[i]-97;
 57         if (!pos->nex[d])
 58         {
 59             p=new rec();
 60             pos->nex[d]=p;
 61         }
 62         pos=pos->nex[d];
 63     }
 64     if (!pos->num)
 65     {
 66         pos->num=++num;
 67         for (i=0;i<len;i++)
 68             if (str[i]=='a' || str[i]=='e' || str[i]=='i' || str[i]=='o' || str[i]=='u')
 69                 x++;
 70         value[num]={x,len};
 71     }
 72     return pos->num;
 73 }
 74  
 75 void tarjan(int d)
 76 {
 77     dfn[d]=low[d]=++ind;
 78     st[++cnt_st]=d;
 79     vis[d]=1;
 80     node *p=e[d];
 81     int dd;
 82     while (p)
 83     {
 84         dd=p->d;
 85         if (!vis[dd])
 86         {
 87             tarjan(dd);
 88             low[d]=min(low[d],low[dd]);
 89         }
 90         else if (!vis_st[dd])
 91             low[d]=min(low[d],dfn[dd]);
 92         p=p->to;
 93     }
 94     if (dfn[d]==low[d])
 95     {
 96         cnt_group++;
 97         va={inf,inf};
 98         while (st[cnt_st]!=d)
 99         {
100             va=min(va,value[st[cnt_st]]);
101             vis_st[st[cnt_st]]=1;
102             group[st[cnt_st--]]=cnt_group;
103         }
104         va=min(va,value[st[cnt_st]]);
105         vis_st[st[cnt_st]]=1;
106         group[st[cnt_st--]]=cnt_group;
107         group_value[cnt_group]=va;
108     }
109 }
110  
111 void dfs(int d)
112 {
113     node *p=e[d];
114     int dd;
115     vis[d]=1;
116     while (p)
117     {
118         dd=p->d;
119         if (!vis[dd])
120             dfs(dd);
121         group_value[group[d]]=min(group_value[group[d]],group_value[group[dd]]);
122         p=p->to;
123     }
124 }
125  
126 int main()
127 {
128     node *p;
129     int n,m,i,x,y;
130     ll totx,toty;
131     tr=new rec();
132     scanf("%d",&n);
133     for (i=1;i<=n;i++)
134     {
135         x=build();
136         b[i]=x;///有可能重复
137     }
138  
139     scanf("%d",&m);
140     for (i=1;i<=m;i++)
141     {
142         x=build();
143         y=build();
144         p=new node();
145         p->d=y;
146         p->to=e[x];
147         e[x]=p;
148     }
149  
150     for (i=1;i<=num;i++)
151         if (!vis[i])
152             tarjan(i);
153  
154     memset(vis,0,sizeof(vis));
155     for (i=1;i<=num;i++)
156         if (!vis[i])
157             dfs(i);
158  
159     totx=0,toty=0;
160     for (i=1;i<=n;i++)
161         totx+=group_value[group[b[i]]].x , toty+=group_value[group[b[i]]].y;
162     printf("%lld %lld",totx,toty);
163     return 0;
164 }
165 /*
166 3
167 a b c
168 3
169 a i
170 b a
171 c a
172  
173 4
174 a e i e
175 3
176 a e
177 e i
178 i a
179  
180  
181 4
182 a a aaa aaaa
183 4
184 a aaaa
185 aaaa aaa
186 aaa aa
187 aa aaaa
188  
189  
190 5
191 b a e i u
192 6
193 a e
194 e i
195 i a
196 i u
197 u b
198 b u
199 */

代码2

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10 #include <map>
 11 
 12 const double eps=1e-8;
 13 const ll inf=1e9;
 14 const ll mod=1e9+7;
 15 const int maxn=3e5+10;  ///larger
 16 const int maxlen=5e5+10;
 17 
 18 ll chu[5]={998244353,469762049,167772161,10000019,10000079};
 19 ll cnt_chu=5,value[5];
 20 char str[maxlen];
 21 int id=0;
 22 
 23 struct node
 24 {
 25     ll v[5];
 26     ll vx,vy;
 27     ///同时也是map的排序方法
 28     bool operator<(const node &b) const
 29     {
 30         if (vx<b.vx)
 31             return 0;
 32         else if (vx>b.vx)
 33             return 1;
 34         if (vy<b.vy)
 35             return 0;
 36         else if (vy>b.vy)
 37             return 1;
 38         for (int i=0;i<5;i++)
 39             if (v[i]<b.v[i])
 40                 return 0;
 41             else if (v[i]>b.v[i])
 42                 return 1;
 43         return 0;///actually won't work
 44     }
 45     bool operator<<(const node &b) const
 46     {
 47         if (vx==b.vx)
 48             return vy<b.vy;
 49         return vx<b.vx;
 50     }
 51     node operator+(const node &b) const
 52     {
 53         node z;
 54         z.vx=vx+b.vx;
 55         z.vy=vy+b.vy;
 56         return z;
 57     }
 58 }ask[maxn],cost[maxn];
 59 
 60 map<node,int> num;
 61 
 62 struct rec
 63 {
 64     node x,y;
 65     bool operator<(const rec &b) const
 66     {
 67         return y<<b.y;///
 68     }
 69 }rule[maxn];
 70 
 71 struct point
 72 {
 73     int d;
 74     point* to;
 75 }*e[maxn];
 76 
 77 int q[maxn];
 78 bool vis[maxn];
 79 
 80 void work(node &z)
 81 {
 82     int len,j,k,vx=0;
 83     scanf("%s",str);
 84     len=strlen(str);
 85 
 86     for (k=0;k<cnt_chu;k++)
 87     {
 88         value[k]=0;
 89         ///'a':1 *27
 90         for (j=0;j<len;j++)
 91             value[k]=(value[k]*27+str[j]-97+1)%chu[k];
 92     }
 93     for (j=0;j<len;j++)
 94         if (str[j]=='a' || str[j]=='e' || str[j]=='i' || str[j]=='o' || str[j]=='u')
 95             vx++;
 96     z.vx=vx;
 97     z.vy=len;
 98     for (j=0;j<cnt_chu;j++)
 99         z.v[j]=value[j];
100 
101     if (num.find(z)==num.end())
102     {
103         num[z]=++id;
104         cost[id]=z;
105     }
106 }
107 
108 int main()
109 {
110     point *p;
111     node r;
112     int n,m,i,j,x,y,head,tail,d;
113     scanf("%d",&n);
114     for (i=1;i<=n;i++)
115         work(ask[i]);
116 
117     scanf("%d",&m);
118     for (i=1;i<=m;i++)
119     {
120         work(rule[i].x);
121         work(rule[i].y);
122         ///反边 通过访问，一个字符串可以到达的所有字符串
123         x=num[rule[i].x];
124         y=num[rule[i].y];
125         if (x!=y)
126         {
127             p=new point();
128             p->d=x;
129             p->to=e[y];
130             e[y]=p;
131         }
132     }
133     sort(rule+1,rule+m+1);
134     for (i=1;i<=m;i++)
135         if (!vis[num[rule[i].y]])
136         {
137             vis[num[rule[i].y]]=1;
138             head=0,tail=1;
139             q[1]=num[rule[i].y];
140             while (head<tail)
141             {
142                 head++;
143                 d=q[head];
144                 p=e[d];
145                 while (p)
146                 {
147                     if (!vis[p->d])
148                     {
149                         q[++tail]=p->d;
150                         vis[p->d]=1;
151                     }
152                     p=p->to;
153                 }
154             }
155             for (j=1;j<=tail;j++)
156                 if (rule[i].y<<cost[q[j]])///
157                     cost[q[j]]=rule[i].y;
158         }
159 
160     r.vx=0,r.vy=0;
161     for (i=1;i<=n;i++)
162         if (ask[i]<<cost[num[ask[i]]])///
163             r=r+ask[i];
164         else
165             r=r+cost[num[ask[i]]];
166 
167     printf("%lld %lld",r.vx,r.vy);
168     return 0;
169 }
170 /*
171 3 a a a
172 1
173 a a
174 
175 1
176 aaa
177 1
178 bbb aaa
179 
180 1
181 aaab
182 2
183 aaab aaaaab
184 aaaaab aabb
185 
186 
187 1
188 aaab
189 2
190 aaaaab aabb
191 aaab aaaaab
192 
193 
194 1
195 ab
196 3
197 ab aab
198 aab aaab
199 aaab bbbbbbbbbbbbb
200 
201 环
202 1 aaa
203 2
204 aaa aaa
205 aaa aaa
206 
207 
208 
209 4
210 ab ab aab aaaa
211 3
212 ab aab
213 aab aaab
214 aaab bbbbbbbbbbbbb
215 
216 1
217 a
218 1
219 aa bb
220 
221 
222 1
223 aaaa
224 0
225 
226 1
227 aaaa
228 1
229 aaaa aaaaa
230 
231 1
232 aaaa
233 1
234 aaaa aaa
235 
236 2
237 a b
238 2
239 a b
240 b a
241 
242 3
243 a e i
244 3
245 a e
246 e i
247 i a
248 
249 */
250 /*
251 如果结构体'<'写错了
252 两个不同/相同的结构体被认为是相同/不同的结构体
253 https://www.cnblogs.com/cmyg/p/11252867.html
254 
255 每个数依次输出编号
256 num=1
257 num=2
258 num=3
259 num=4
260 num=3
261 num=4
262 num=5
263 num=6
264 num=7
265 num=3
266 num=4
267 num=8
268 num=9
269 num=10
270 num=11
271 
272 500
273 aaavakaumfjbaujybvgapjxlis eawsmkalasfa d o l
274 */

IMatrix Again

f(x) 递增 / 0/1不能/能实现，则为0 0 0 0... 0 1 1 ... 1

求最小数值：二分

求若干个a*b的矩阵的属性

两个单调队列是常规操作

如 https://www.cnblogs.com/cmyg/p/11205042.html E题

第一次求出若干个a*1，

第二次求出若干个a*b(由b个a*1组成)

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10  
 11 const int maxn=5e2+10;
 12 const double eps=1e-8;
 13 const ll inf=1e9;
 14  
 15 ///二维线段树是否可行
 16  
 17 int n,m,g;
 18 int a[maxn][maxn],x[maxn][maxn],y[maxn];
 19 int headx[maxn],tailx[maxn],heady,taily,vmax[maxn][maxn];
 20  
 21 bool work(int l)
 22 {
 23     int i,j;
 24  
 25     ///max
 26     for (j=1;j<=m;j++)
 27         headx[j]=1,tailx[j]=0;
 28  
 29     for (i=1;i<=n;i++)
 30     {
 31         heady=1,taily=0;
 32  
 33         for (j=1;j<=m;j++)
 34         {
 35             while (headx[j]<=tailx[j] && x[j][headx[j]]<=i-l)
 36                 headx[j]++;
 37             while (headx[j]<=tailx[j] && a[x[j][tailx[j]]][j]<=a[i][j])
 38                 tailx[j]--;
 39             x[j][++tailx[j]]=i;
 40  
 41             while (heady<=taily && y[heady]<=j-l)
 42                 heady++;
 43             while (heady<=taily && a[ x[y[taily]][headx[y[taily]]] ][y[taily]] <= a[ x[j][headx[j]] ][j])
 44                 taily--;
 45             y[++taily]=j;
 46  
 47             if (i>=l && j>=l)
 48                 vmax[i][j]=a[ x[y[heady]][headx[y[heady]]] ][y[heady]];
 49  
 50         }
 51     }
 52  
 53     ///min
 54     for (j=1;j<=m;j++)
 55         headx[j]=1,tailx[j]=0;
 56  
 57     for (i=1;i<=n;i++)
 58     {
 59         heady=1,taily=0;
 60  
 61         for (j=1;j<=m;j++)
 62         {
 63             while (headx[j]<=tailx[j] && x[j][headx[j]]<=i-l)
 64                 headx[j]++;
 65             while (headx[j]<=tailx[j] && a[x[j][tailx[j]]][j]>=a[i][j])
 66                 tailx[j]--;
 67             x[j][++tailx[j]]=i;
 68  
 69             while (heady<=taily && y[heady]<=j-l)
 70                 heady++;
 71             while (heady<=taily && a[ x[y[taily]][headx[y[taily]]] ][y[taily]] >= a[ x[j][headx[j]] ][j])
 72                 taily--;
 73             y[++taily]=j;
 74  
 75             if (i>=l && j>=l && vmax[i][j]-a[ x[y[heady]][headx[y[heady]]] ][y[heady]] <=g )
 76                 return 1;
 77  
 78         }
 79     }
 80  
 81     return 0;
 82 }
 83  
 84 int main()
 85 {
 86     int i,j,l,r,M;
 87     scanf("%d%d%d",&n,&m,&g);
 88     for (i=1;i<=n;i++)
 89         for (j=1;j<=m;j++)
 90             scanf("%d",&a[i][j]);
 91     l=1,r=min(n,m);
 92     while (l<=r)
 93     {
 94         M=(l+r)>>1;
 95         if (work(M))
 96             l=M+1;
 97         else
 98             r=M-1;
 99     }
100     printf("%d",r);
101     return 0;
102 }

JMex

对数字进行排序

证明：

a1,...,ak 能表示 1~x

对于a_{k+1}

若a_{k+1} > x+1，则不能表示的最小数为x+1

若a_{k+1} <= x+1

则a_{k+1} 加上 1~x，能表示1 +a_{k+1} ~ x + a_{k+1}

再包含集合1~x，即能表示1~x+a_{k+1}。

 1 #include <cstdio>
 2 #include <cstdlib>
 3 #include <cmath>
 4 #include <cstring>
 5 #include <string>
 6 #include <set>
 7 #include <map>
 8 #include <list>
 9 #include <queue>
10 #include <bitset>
11 #include <vector>
12 #include <algorithm>
13 #include <iostream>
14 using namespace std;
15   
16 #define ll long long
17 const int maxn=1e5+10;
18 const ll inf=1e9+7;
19 const double eps=1e-8;
20   
21 ll a[maxn];
22   
23 int main()
24 {
25     int n,i;
26     ll sum=0;
27     scanf("%d",&n);
28     for (i=1;i<=n;i++)
29         scanf("%lld",&a[i]);
30     sort(a+1,a+n+1);
31     sum=0;
32     for (i=1;i<=n;i++)
33     {
34         if (a[i]>sum+1)
35         {
36             printf("%lld",sum+1);
37             break;
38         }
39         sum+=a[i];
40     }
41     if (i==n+1)
42         printf("%lld",sum+1);
43     return 0;
44 }

KMoney

费用流

设置连边/边值是常规操作

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <iostream>
  8 using namespace std;
  9 #define ll long long
 10  
 11 const double eps=1e-8;
 12 const ll inf=1e18;
 13 const ll mod=1e9+7;
 14 const int maxn=1e2+10;///*2 point
 15  
 16 ll flow,fee;
 17  
 18 struct node
 19 {
 20     ll d,len,cost;
 21     node *to,*opp;
 22 }*e[maxn],*pre[maxn];
 23  
 24 int ss,tt;
 25 ll dis[maxn][maxn],dist[maxn],add[maxn];
 26 int g[maxn],l[maxn],r[maxn],q[maxn];
 27 bool vis[maxn];
 28  
 29 void addedge(int a,int b,ll c,ll d)
 30 {
 31     node *p,*q;
 32     p=new node();
 33     q=new node();
 34     p->d=b;
 35     p->len=c;
 36     p->cost=d;
 37     p->opp=q;
 38     p->to=e[a];
 39     e[a]=p;
 40  
 41     q->d=a;
 42     q->len=0;
 43     q->cost=-d;
 44     q->opp=p;
 45     q->to=e[b];
 46     e[b]=q;
 47 }
 48  
 49 void bfs()
 50 {
 51     node *p;
 52     int head,tail,d,dd;
 53     while (1)
 54     {
 55         memset(vis,0,sizeof(vis));
 56         memset(dist,0x7f,sizeof(dist));
 57         dist[ss]=0;
 58         add[ss]=inf;
 59         head=0,tail=1;
 60         q[1]=ss,vis[ss]=1;
 61         while (head!=tail)
 62         {
 63             head=(head+1)%maxn;
 64             d=q[head];
 65             p=e[d];
 66             while (p)
 67             {
 68                 dd=p->d;
 69                 if (p->len && dist[dd]>dist[d]+p->cost)
 70                 {
 71                     add[dd]=min(add[d],p->len);
 72                     dist[dd]=dist[d]+p->cost;
 73                     pre[dd]=p->opp;
 74                     if (!vis[dd])
 75                     {
 76                         tail=(tail+1)%maxn;
 77                         q[tail]=dd;
 78                         vis[dd]=1;
 79                     }
 80                 }
 81                 p=p->to;
 82             }
 83             vis[d]=0;
 84         }
 85         if (dist[tt]==dist[maxn-1])
 86             return;
 87  
 88         flow+=add[tt];
 89         fee+=add[tt]*dist[tt];
 90         d=tt;
 91 //        printf("add=%lld dist=%lld\n",add[tt],dist[tt]);
 92         while (d!=ss)
 93         {
 94 //            printf("%d ",d);
 95             pre[d]->len+=add[tt];
 96             pre[d]->opp->len-=add[tt];
 97             d=pre[d]->d;
 98         }
 99 //        printf("\n");
100     }
101 }
102  
103 int main()
104 {
105     int n,m,k,a,b,c,i,j,price;
106     scanf("%d%d",&n,&m);
107     ss=0,tt=2*n+1;
108     for (i=1;i<=n;i++)
109     {
110         scanf("%d%d%d%lld",&l[i],&r[i],&g[i],&price);
111         addedge(ss,i,inf,price);
112         addedge(i,tt,g[i],0);
113         addedge(0,i+n,g[i],0);
114     }
115  
116     for (i=1;i<=n;i++)
117         for (j=1;j<=n;j++)
118             if (i!=j)
119                 dis[i][j]=inf;
120     while (m--)
121     {
122         scanf("%d%d%d",&a,&b,&c);
123         dis[a][b]=dis[b][a]=c;
124     }
125  
126     for (k=1;k<=n;k++)
127         for (i=1;i<=n;i++)
128             for (j=1;j<=n;j++)
129                 if (dis[i][j]>dis[i][k]+dis[k][j])
130                     dis[i][j]=dis[i][k]+dis[k][j];
131     ///i->j
132     for (i=1;i<=n;i++)
133         for (j=1;j<=n;j++)
134             if (i!=j && dis[i][j]!=inf && r[i]<l[j])
135                 addedge(i+n,j,g[i],dis[i][j]);
136  
137     bfs();
138     printf("%lld",fee);
139     return 0;
140 }

posted @ 2019-04-21 22:17 congmingyige 阅读(127) 评论(0) 编辑收藏举报

刷新页面返回顶部

congmingyige

Minieye杯第十五届华中科技大学程序设计邀请赛现场同步赛

公告