点分治
点分治
树结构
可以被分成两半求,再合起来的
求路径长度,满足某些特性的字符/数
P3806 【模板】点分治1
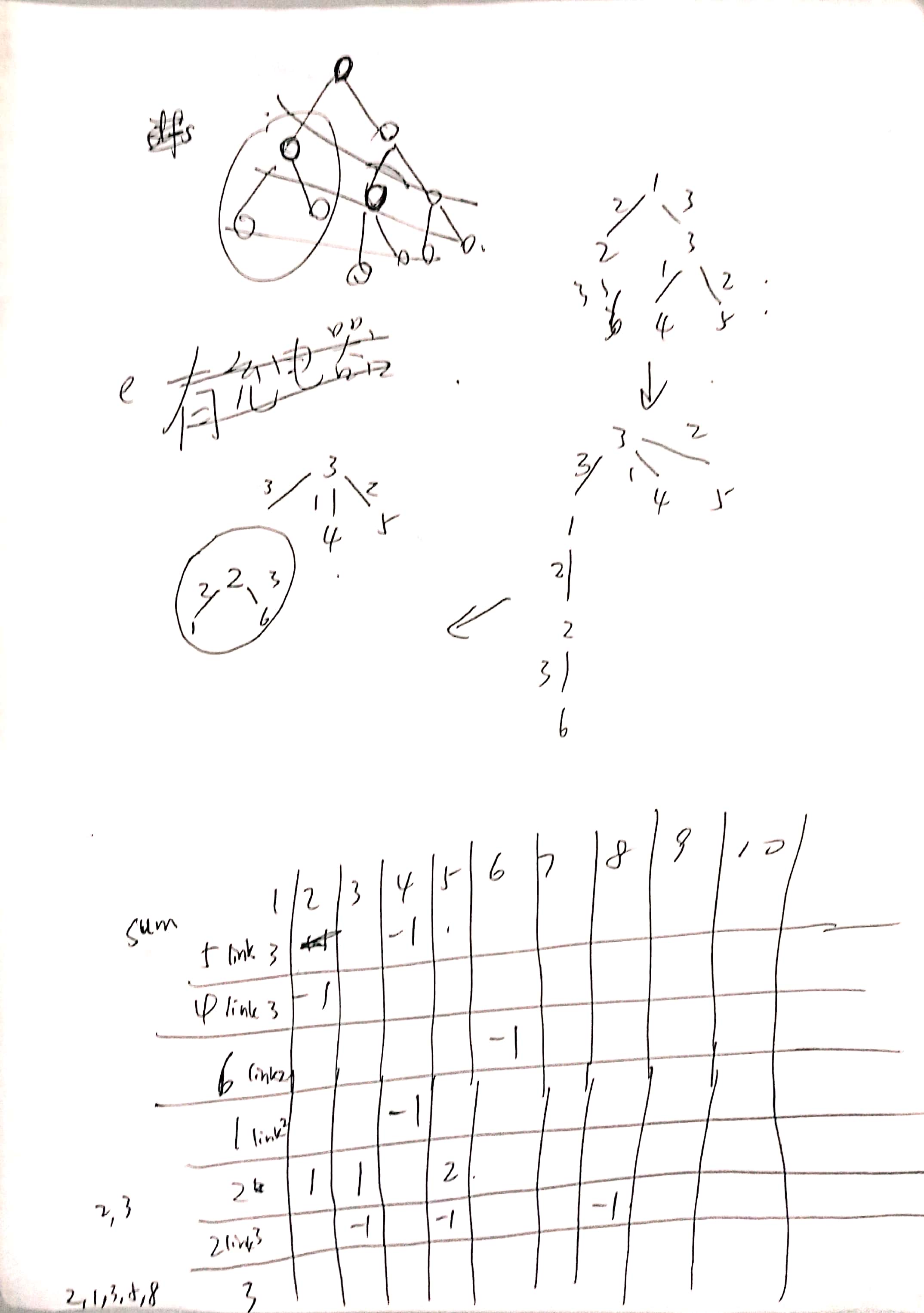

用father数组,判断从一个点出发访问另外一个点(另外一个点是否访问,另外一个点是否是这个点的父亲)
clrdist 减少重复部分
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cmath> 4 #include <cstring> 5 #include <string> 6 #include <algorithm> 7 #include <set> 8 #include <map> 9 #include <queue> 10 #include <iostream> 11 using namespace std; 12 13 #define ll long long 14 15 const int maxn=1e4+10; 16 const int maxq=1e2+10; 17 const int maxvalue=1e7+10; 18 const int inf=1e9; 19 const double eps=1e-8; 20 21 /* 22 找重心 23 子树再找重心 24 根,子树(s) 间的操作 25 可能要除去单个子树内两个结点的重复 26 */ 27 28 struct node 29 { 30 int d,len; 31 node *to; 32 }*e[maxn]; 33 34 ll sum[maxq]; ///in case 35 int query[maxq],siz[maxn],q,nn; 36 int curroot,mins,clrdist[maxn],fa[maxn]; 37 int exist[maxvalue]; 38 bool has[maxn]; 39 40 void dfs(int d) 41 { 42 int dd,maxsiz=0; 43 siz[d]=1; 44 node *p=e[d]; 45 while (p) 46 { 47 dd=p->d; 48 if (fa[d]!=dd && !has[dd]) 49 { 50 fa[dd]=d; 51 dfs(dd); 52 maxsiz=max(maxsiz,siz[dd]); 53 siz[d]+=siz[dd]; 54 } 55 p=p->to; 56 } 57 maxsiz=max(maxsiz,nn-siz[d]); 58 if (maxsiz<mins) 59 mins=maxsiz,curroot=d; 60 } 61 62 void finddist(int d,int dis) 63 { 64 int dd; 65 clrdist[++clrdist[0]]=dis; 66 node *p=e[d]; 67 while (p) 68 { 69 dd=p->d; 70 if (fa[d]!=dd && !has[dd]) 71 finddist(dd,dis+p->len); 72 p=p->to; 73 } 74 } 75 76 void work(int d) 77 { 78 int root,dd,i,j,preind,firind; 79 firind=clrdist[0]; 80 mins=inf; ///10000 * 10000 81 nn=siz[d],dfs(d); 82 root=curroot; 83 has[root]=1; 84 if (d!=root) 85 siz[d]=nn-siz[root]; /// 86 87 node *p=e[root]; 88 while (p) 89 { 90 dd=p->d; 91 if (!has[dd]) 92 { 93 work(dd); 94 preind=clrdist[0]; 95 finddist(dd,p->len); 96 for (i=preind+1;i<=clrdist[0];i++) 97 exist[clrdist[i]]++; 98 99 for (i=preind+1;i<=clrdist[0];i++) 100 for (j=1;j<=q;j++) 101 if (query[j]>clrdist[i]) 102 sum[j]-=exist[clrdist[i]]*exist[query[j]-clrdist[i]]; 103 104 for (i=preind+1;i<=clrdist[0];i++) 105 exist[clrdist[i]]--; 106 107 } 108 p=p->to; 109 } 110 111 for (i=firind+1;i<=clrdist[0];i++) 112 exist[clrdist[i]]++; 113 114 for (i=firind+1;i<=clrdist[0];i++) 115 for (j=1;j<=q;j++) 116 if (query[j]>=clrdist[i]) 117 sum[j]+=exist[clrdist[i]]*exist[query[j]-clrdist[i]]; 118 ///这里多算了 119 ///v+v=query[i] -exist[v] 120 ///相同的只要计算一次exist[v](重复多次)*exist[query[i]-v] 121 ///exist[p]*exist[q] exist[q]*exist[p] 重复 122 123 for (i=firind+1;i<=clrdist[0];i++) 124 exist[clrdist[i]]--; 125 clrdist[0]=firind; 126 127 has[root]=0; ///取消不能走的限制 128 } 129 130 int main() 131 { 132 node *p; 133 int n,i,a,b,c; 134 scanf("%d%d",&n,&q); 135 for (i=1;i<n;i++) 136 { 137 scanf("%d%d%d",&a,&b,&c); 138 p=new node(); 139 p->d=b; 140 p->len=c; 141 p->to=e[a]; 142 e[a]=p; 143 144 p=new node(); 145 p->d=a; 146 p->len=c; 147 p->to=e[b]; 148 e[b]=p; 149 } 150 for (i=1;i<=q;i++) 151 scanf("%d",&query[i]); 152 153 exist[0]=1; 154 siz[1]=n,work(1); 155 156 for (i=1;i<=q;i++) 157 if (sum[i]==0) 158 printf("NAY\n"); 159 else 160 printf("AYE\n"); 161 return 0; 162 } 163 /* 164 6 15 165 1 2 2 166 1 3 3 167 2 6 3 168 3 4 1 169 3 5 2 170 1 171 2 172 3 173 4 174 5 175 6 176 7 177 8 178 9 179 10 180 11 181 12 182 13 183 14 184 15 185 186 6 15 187 1 2 1 188 1 3 3 189 1 4 4 190 1 5 7 191 5 6 1 192 1 193 2 194 3 195 4 196 5 197 6 198 7 199 8 200 9 201 10 202 11 203 12 204 13 205 14 206 15 207 */
用了vis数组,每次使用需要初始化,不太方便
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cmath> 4 #include <cstring> 5 #include <string> 6 #include <algorithm> 7 #include <set> 8 #include <map> 9 #include <queue> 10 #include <iostream> 11 using namespace std; 12 13 #define ll long long 14 15 const int maxn=1e4+10; 16 const int maxq=1e2+10; 17 const int maxvalue=1e7+10; 18 const int inf=1e9; 19 const double eps=1e-8; 20 21 /* 22 找重心 23 子树再找重心 24 根,子树(s) 间的操作 25 可能要除去单个子树内两个结点的重复 26 */ 27 28 struct node 29 { 30 int d,len; 31 node *to; 32 }*e[maxn]; 33 34 ll sum[maxq]; ///in case 35 int query[maxq],siz[maxn],q,nn; 36 int curroot,mins,clrvis[maxn],clrdist[maxn]; 37 int exist[maxvalue]; 38 bool has[maxn],vis[maxn]; 39 40 void dfs(int d) 41 { 42 int dd,maxsiz=0; 43 siz[d]=1; 44 clrvis[++clrvis[0]]=d; 45 vis[d]=1; 46 node *p=e[d]; 47 while (p) 48 { 49 dd=p->d; 50 if (!vis[dd] && !has[dd]) 51 { 52 dfs(dd); 53 maxsiz=max(maxsiz,siz[dd]); 54 siz[d]+=siz[dd]; 55 } 56 p=p->to; 57 } 58 maxsiz=max(maxsiz,nn-siz[d]); 59 if (maxsiz<mins) 60 mins=maxsiz,curroot=d; 61 } 62 63 void finddist(int d,int dis) 64 { 65 int dd; 66 clrvis[++clrvis[0]]=d; 67 vis[d]=1; 68 clrdist[++clrdist[0]]=dis; 69 node *p=e[d]; 70 while (p) 71 { 72 dd=p->d; 73 if (!vis[dd] && !has[dd]) 74 finddist(dd,dis+p->len); 75 p=p->to; 76 } 77 } 78 79 void work(int d) 80 { 81 int root,dd,i,j,preind,firind; 82 firind=clrdist[0]; 83 mins=inf; ///10000 * 10000 84 nn=siz[d],dfs(d); 85 for (i=1;i<=clrvis[0];i++) 86 vis[clrvis[i]]=0; 87 clrvis[0]=0; 88 root=curroot; 89 has[root]=1; 90 if (d!=root) 91 siz[d]=nn-siz[root]; /// 92 93 node *p=e[root]; 94 while (p) 95 { 96 dd=p->d; 97 if (!has[dd]) 98 { 99 work(dd); 100 preind=clrdist[0]; 101 finddist(dd,p->len); 102 for (i=1;i<=clrvis[0];i++) 103 vis[clrvis[i]]=0; 104 clrvis[0]=0; 105 106 for (i=preind+1;i<=clrdist[0];i++) 107 exist[clrdist[i]]++; 108 109 for (i=preind+1;i<=clrdist[0];i++) 110 for (j=1;j<=q;j++) 111 if (query[j]>clrdist[i]) 112 sum[j]-=exist[clrdist[i]]*exist[query[j]-clrdist[i]]; 113 114 for (i=preind+1;i<=clrdist[0];i++) 115 exist[clrdist[i]]--; 116 117 } 118 p=p->to; 119 } 120 121 for (i=firind+1;i<=clrdist[0];i++) 122 exist[clrdist[i]]++; 123 124 for (i=firind+1;i<=clrdist[0];i++) 125 for (j=1;j<=q;j++) 126 if (query[j]>=clrdist[i]) 127 sum[j]+=exist[clrdist[i]]*exist[query[j]-clrdist[i]]; 128 ///这里多算了 129 ///v+v=query[i] -exist[v] 130 ///相同的只要计算一次exist[v](重复多次)*exist[query[i]-v] 131 ///exist[p]*exist[q] exist[q]*exist[p] 重复 132 133 for (i=firind+1;i<=clrdist[0];i++) 134 exist[clrdist[i]]--; 135 clrdist[0]=firind; 136 137 has[root]=0; ///取消不能走的限制 138 } 139 140 int main() 141 { 142 node *p; 143 int n,i,a,b,c; 144 scanf("%d%d",&n,&q); 145 for (i=1;i<n;i++) 146 { 147 scanf("%d%d%d",&a,&b,&c); 148 p=new node(); 149 p->d=b; 150 p->len=c; 151 p->to=e[a]; 152 e[a]=p; 153 154 p=new node(); 155 p->d=a; 156 p->len=c; 157 p->to=e[b]; 158 e[b]=p; 159 } 160 for (i=1;i<=q;i++) 161 scanf("%d",&query[i]); 162 163 exist[0]=1; 164 siz[1]=n,work(1); 165 166 for (i=1;i<=q;i++) 167 if (sum[i]==0) 168 printf("NAY\n"); 169 else 170 printf("AYE\n"); 171 return 0; 172 } 173 /* 174 6 15 175 1 2 2 176 1 3 3 177 2 6 3 178 3 4 1 179 3 5 2 180 1 181 2 182 3 183 4 184 5 185 6 186 7 187 8 188 9 189 10 190 11 191 12 192 13 193 14 194 15 195 196 6 15 197 1 2 1 198 1 3 3 199 1 4 4 200 1 5 7 201 5 6 1 202 1 203 2 204 3 205 4 206 5 207 6 208 7 209 8 210 9 211 10 212 11 213 12 214 13 215 14 216 15 217 */



