KMP（快速模式串匹配）
KMP（快速模式串匹配）
概述
KMP算法是一种高效的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出，所以称作KMP算法 快（K）速模（M）式串匹（P）配
理解
要求模式串在主串中的匹配次数，直接暴力枚举每两个位置是否一样，时间复杂度 \(\Theta(nm)\)，显然无法接受，那么怎么优化呢？
暴力算法中每次两个指针分别指向两个字符串，一旦不匹配，主串指针回滚到开始匹配的字符的下一个，模式串指针回滚到开头，但是真的有必要吗？我们已经确认了两个指针所指向的字符第一次不匹配的地方前面的所有字符都是相同的，那么当遇到不匹配的时候能不能不从头开始，而是从某个特定的地方开始来让匹配更快呢？
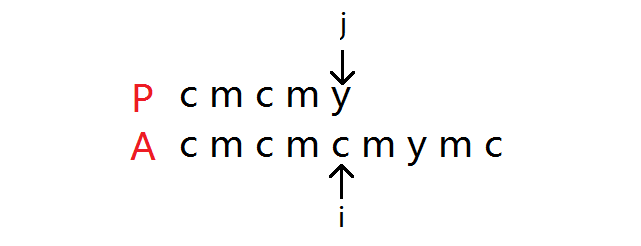
例如图中的这种情况，此时发现主串与模式串不匹配，暴力算法会将 \(i\) 回滚到第二个字符，将 \(j\) 指向模式串开头来重新匹配，但是这是并不必要的，因为我们已经知道了主串的 \(i\) 前的 \(4\) 个字符和模式串的 \(j\) 前的 \(4\) 个字符是相等的，这时只要把 \(j\) 回到指向第三个字符，\(i\) 不动即可，减少了很多匹配次数，如下图
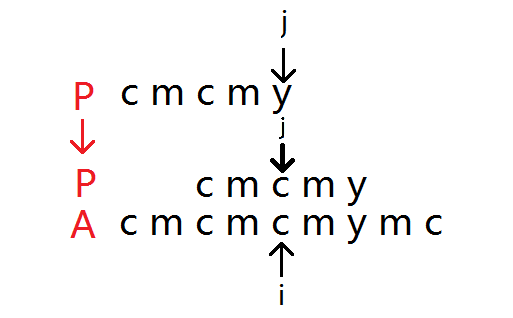
为了实现这一操作，KMP 算法引入了一个新的数组 \(\text{next}\)，它存储着模式串匹配到某个位置不匹配时应该回退到哪个地方， \(\text{next}\) 数组的具体含义就是：\(\text{next}_i\) 表示在模式串中前 \(i\) 个字符组成的字符串的最长公共前后缀长度，也就是前 \(i\) 个字符组成的字符串的前缀和后缀的交集中长度最长的那一个
例如字符串 \(\text{cmcmy}\)，它的前缀有 \(\text{c,cm,cmc,cmcm}\)（注意一个字符串的前后缀均不包括它自身），后缀有 \(\text{y,my,cmy,mcmy}\)，它们的交集为空集，于是乎 \(\text{next}_5=0\)，它的前四个字符的前缀有 \(\text{c,cm,cmc}\)，后缀有 \(\text{m,cm,mcm}\) 交集有 \(\text{cm}\)，最长的长度为 \(2\)，所以 \(\text{next}_4=2\)
当遇到不匹配时，根据 \(\text{next}\) 数组移动两个指针就能节省很多不必要的操作
next 数组预处理
预处理 \(\text{next}\) 数组就是计算前缀函数，关于前缀函数计算的优化过程这里就不多赘述，直接给出终极版本，感兴趣的读者可以去查阅相关资料
预处理 \(\text{next}\) 数组其实就是 \(\text{next}\) 数组和自己匹配，将子串的前缀后缀对齐，看一样的最长有多长就行
显然我们知道 \(\text{next}_1=0\)
我们使用一个指针 \(i\) 指向模式串第 \(i\) 位，从第 \(2\) 位开始计算，表示当前正在求算 \(\text{next}_i\)
显然 \(\text{next}_i\) 至多比 \(\text{next}_{i-1}\) 大 \(1\)，如果 \(\text{next}_i=\text{next}_{i-1}+1\) 就说明此时的最长公共前缀比上次的增加了 \(1\)，那么就说明模式串的第 \(i\) 位与第 \(\text{next}_{i-1}+1\) 位相等，所以我们可以说如果模式串的第 \(i\) 位与第 \(\text{next}_{i-1}+1\) 位相等就有 \(\text{next}_i=\text{next}_{i-1}+1\)
如果不相等那么也不一定 \(\text{next}_i=0\)，因为模式串的前 \(i-1\) 个字符中的长度为 \(\text{next}_{i-1}\) 的前后缀是一样的，如果模式串的第 \(i\) 个字符与第 \(\text{next}_{\text{next}_{i-1}}+1\) 个字符一样那么不难发现 \(\text{next}_i=\text{next}_{\text{next}_{i-1}}+1\)，于是乎我们就继续计算模式串的第 \(i\) 位是否与第 \(\text{next}_{\text{next}_{i-1}}+1\) 位一样，以此类推，直到找到一样的字符或是 \(\text{next}\) 数组中的对应值已经变为 \(0\)，如果是 \(\text{next}\) 数组中的对应值已经为 \(0\)，那么 \(\text{next}_i=0\)
char p[MAXN],nxt[MAXN];
void init()
{
int plen=strlen(p+1);//获取字符串长度
for(int i=2,j=0;i<=plen;i++)//枚举i，而j从next[1]即0开始
{
//此时j仍然等于上一轮循环的next[i-1]
while(j&&p[i]!=p[j+1]) j=nxt[j];//只要不相等或者没到0就继续往回跳
if(p[i]==p[j+1]) nxt[i]=++j;//相等就把j向后挪一位并赋值给next
else nxt[i]=0;//不相等就是没有匹配，next=0
}
}
这样做的时间复杂度是多少呢？上面的代码每一层 for 循环中 \(j\) 至多只会增加 \(1\)，所以 \(j\) 最多只会增加 \(n\)，在 while 中每一次 \(j\) 至少会减少 \(1\)（根据 \(\text{next}\) 的定义），而 \(j\) 始终非负，所以 \(j\) 也至多减少 \(n\)，复杂度即为 \(\Theta(n)\)
匹配
每次一旦在 \(j\) 处不匹配，只要 \(j\ne0\) 就将 \(j\) 移动到 \(\text{next}_j+1\) 再判断，否则就把 \(i\) 移动到 \(i+1\)，这样就能一直匹配下去
char s[MAXN],p[MAXN],nxt[MAXN];
void kmp()
{
int slen=strlen(s+1),plen=strlen(p+1);//获取字符串长度
for(int i=1,j=0;i<=slen;i++)//枚举主串指针，j从next[1]也就是0开始
{
while(j&&p[j+1]!=s[i]) j=nxt[j];//如果不匹配就往前找直到匹配或者到模式串开头
if(s[i]==p[j+1]) j++;//匹配成功就往后多挪一位
if(j==plen)//如果整个模式串都匹配成功
{
printf("%d\n",i-j+1);//输出成功匹配起点的位置
j=nxt[j];//继续往前跳
}
}
}
类似于预处理的复杂度分析方法，匹配的复杂度为 \(\Theta(m)\)
整个 KMP 算法的复杂度即为 \(\Theta(n+m)\)
