ARIMa--时间序列模型
一、概述
在生产和科学研究中,对某一个或者一组变量 x(t)x(t) 进行观察测量,将在一系列时刻 t1,t2,⋯,tnt1,t2,⋯,tn 所得到的离散数字组成的序列集合,称之为时间序列。
时间序列分析是根据系统观察得到的时间序列数据,通过曲线拟合和参数估计来建立数学模型的理论和方法。时间序列分析常用于国民宏观经济控制、市场潜力预测、气象预测、农作物害虫灾害预报等各个方面。
ARIMA模型,全称为自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model),是由博克思(Box)和詹金斯(Jenkins)于20世纪70年代初提出的一种时间序列预测方法。ARIMA模型是指在将非平稳时间序列转化为平稳时间序列过程中,将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。
注意:时间序列模型适用于做短期预测,即统计序列过去的变化模式还未发生根本性变化。
二、原理
ARIMA(p,d,q) 称为差分自回归移动平均模型,根据原序列是否平稳以及回归中所含部分的不同,包括移动平均过程(MA)、自回归过程(AR)、自回归移动平均过程(ARMA)和自回归滑动平均混合过程(ARIMA)。
AR是自回归,p为自回归项;MA为移动平均,q为移动平均项数,d为时间序列变为平稳时间序列时所做的差分次数。
三、时间序列建模步骤
1.数据的准备,准备带观测系统的时间序列数据
2.数据可视化,观测是否为平稳时间序列,若是非平稳时间序列,则需要进行d阶差分运算,将其化为平稳时间序列
3.得到平稳时间序列后,要对其分别求得自相关系数ACF,偏自相关系数PACF,通过对自相关图和偏自相关图的分析,得到最佳的阶层P,阶数q
4.由以上得到d,p,q,得到ARIMA模型,然后对模型进行模型检验
四、典例解析
1.数据的准备
这里我们已经备好了数据,截图如下。
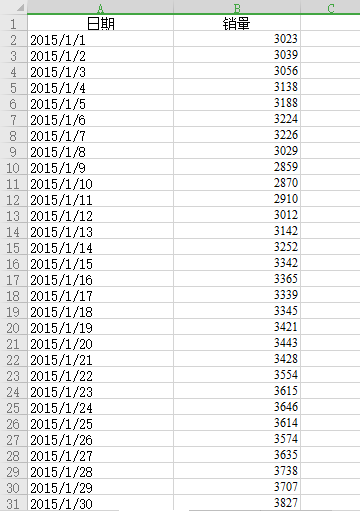
2.数据绘图展示
1 data=pd.read_excel(r".\arima_data.xls",index_col=0) 2 data.plot(figsize=(12, 8)) 3 plt.show()

3.d阶差分分析
ARIMA模型的要求是平稳性的时间序列,但是上图很明显是一个非平稳的时间序列,数据有很明显的线性相关性,这时首先要做的就是差分了,得到一个平稳的时间序列。
如果你对时间序列做d次差分才能得到一个平稳序列,那么可以使用ARIMA(p,d,q)模型,其中d是差分次数。
一阶差分
1 fig = plt.figure(figsize=(8, 5)) 2 # 参数111,指的是将图像分成1行1列,此子图占据从左到右从上到下的1位置。 3 ax1 = fig.add_subplot(111) 4 #做一阶差分 5 diff1 = data.diff(1) 6 diff1.plot(ax=ax1) 7 plt.show()
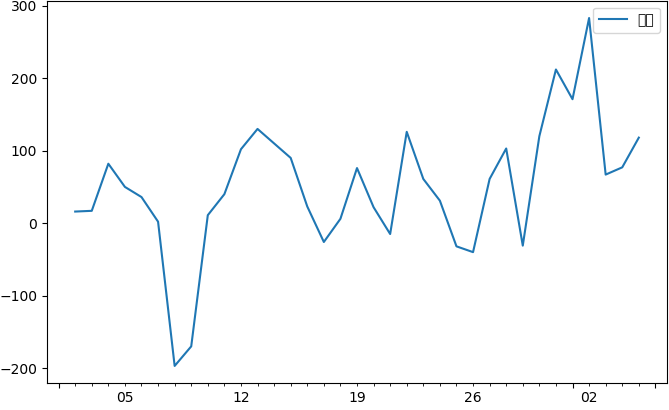
一阶差分的时间序列并不很平稳,我们看一下二阶差分
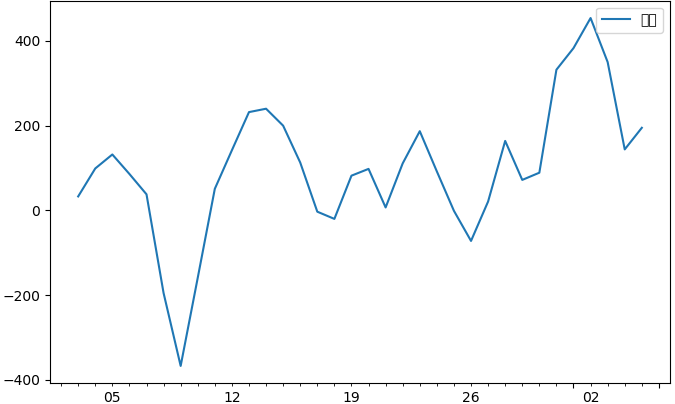
这是我们发现二阶差分明显不如一阶差分,所以这里我们就选定一阶差分,则参数的 d 定为 1.
4.确定合适的p,q的值
绘制平稳时间序列的自相关图和偏自相关图
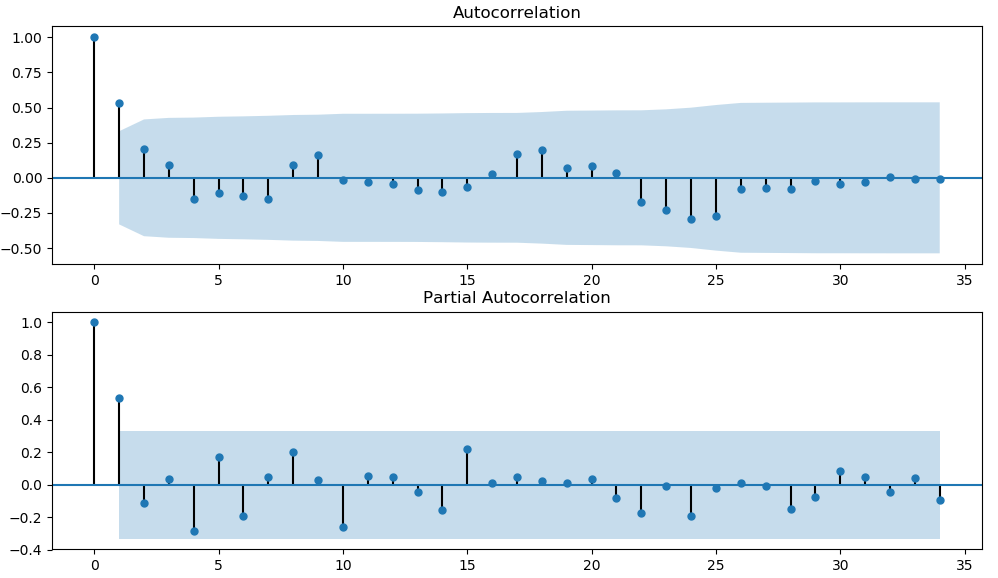
分析自相关系数图和偏自相关系数图,确定P,q的值的依据
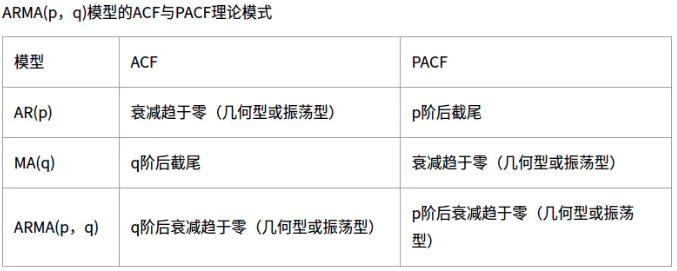
可以看出俩个图都在1阶后衰减趋于0,所以我们就确定了p,q,均为1
5.模型检测
一般模型 是用来检测我们前面几个参数的优劣性的,但是我们这边只有个一个选择,所以就不做测试,给出方法。
采用AIC法则对ARIMA模型进行检测,我们知道:增加自由参数的数目提高了拟合的优良性,AIC鼓励数据拟合的优良性但是尽量避免出现过度拟合(Overfitting)的情况。所以优先考虑的模型应是AIC值最小的那一个。
目前常用的准则:
* AIC=-2 ln(L) + 2 k 中文名字:赤池信息量 akaike information criterion
* BIC=-2 ln(L) + ln(n)*k 中文名字:贝叶斯信息量 bayesian information criterion
* HQ=-2 ln(L) + ln(ln(n))*k hannan-quinn criterion
1 arma_mod20 = sm.tsa.ARMA(dta,(7,0)).fit() 2 print(arma_mod20.aic,arma_mod20.bic,arma_mod20.hqic)
5.模型预测
1 arma_mod20 = ARIMA(data['销量'].astype(float), (1, 1, 1)).fit() 2 # 返回未来n天的结果,预测误差,置信区间 3 print(arma_mod20.forecast(20))

截图只显示了结果,预测误差和置信区间没有展示




