人工智能--第二天--KNN算法实现
一、案例说明
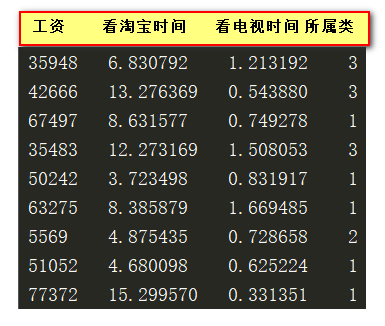
有一份数据,公司让你写一个程序,他告诉我们这个测试数据的的已知条件,我们告诉他这个数据应该在哪一个类别
二、主要构思
1.如何分析该项目,思路产生的过程
1. 不同类别数据之间有没有区别? 假设有
2. 如果有区别,区别在哪? 和年龄,长相等有没有关系?没有关系 区别在工资,淘宝,电视时间
3. 区别在于特征的值 很难直接找到一个或者多个确定的条件来判断数据的类别
4. 能不能找到待预测的数据比较接近的人
如何判断两个样本之间的距离 使用欧式距离
5. 找到距离最近的前k个人 5
6. 统计前k个样本中,出现次数最多的那个类别作为待遇测数据的类别
2.详细设计
1. 读取数据,分离出特征矩阵和目标向量
2. 归一化特征矩阵:最大最小值归一化
3. 计算新样本到所有样本之间的距离 计算方式使用欧式距离或者曼哈顿距离

4. 找到距离新样本最近的前k个样本 k值的选择凭经验 3-15个 最好是奇数
5. 统计出现次数最多的那个类别
6. 将该类别作为新样本的类别输出
3.每个功能的代码实现--Python
1.load方法:读取数据,并分离出特征矩阵和目标向量
1 def load(filename, sep): 2 """ 3 读取元数据,并分离特征矩阵和目标向量 4 :param filename: 源文件路径 5 :return: Feature_matrix,aims_vector 特征矩阵 目标向量 6 """ 7 with open(filename, "r")as f: 8 res = f.readlines() 9 # 先用strip去除\n再用\t分离 10 res = [i.strip().split(sep) for i in res] 11 ##切割特征矩阵和目标向量 一般来说目标向量都在最后一列 12 # 目标向量 13 aims_vector = [i[-1] for i in res] 14 # 特征矩阵 15 Feature_matrix = [i[:-1] for i in res] 16 return Feature_matrix, aims_vector
2.return_only方法:归一化
1 def return_only(X): 2 ###方式一:不使用转置 ,直接改变原矩阵 3 for i in range(len(X[0])): 4 column = [float(x[i]) for x in X] 5 max_c, min_c = max(column), min(column) 6 # 改变原矩阵 7 for j in X: 8 j[i] = (float(j[i]) - min_c) / (max_c - min_c) 9 return X 10 ###方式二:使用矩阵的转置 11 # new_X = [] 12 # for i in range(len(X[0])): 13 # col = [float(x[i]) for x in X] 14 # max_col, min_col = max(col), min(col) 15 # new_col = [(c - min_col) / (max_col - min_col) for c in col] 16 # new_X.append(new_col) 17 # # 外层是转置后的行数,内层是转置后列数 18 # # 双层循环 内层在第一个 外层在第二个 19 # return [[new_X[i][j] for i in range(len(new_X))] for j in range(len(new_X[0]))]
3.class_ify方法 :KNN分类器
1 def class_ify( X, Y, x): 2 """ 3 分类器 4 :param X:特征矩阵 5 :param Y:目标向量 6 :param x:测试数据 7 :return:测试数据的类别 8 """ 9 # 对测试数据x的容错处理 10 x_ = list(x) 11 x_1 = [float(i) for i in x_] 12 # 收集结果的列表 13 res_li = [] 14 # X是二位列表双层循环,第一层(外层)循环每一行,第二层(内层)循环列数,计算欧式距离 15 for i in X: 16 dis_sum = 0 17 for j in range(len(i)): 18 # 计算每个i与x的距离 19 dis_sum += (i[j] - x_1[j]) ** 2 20 dis_sum = dis_sum ** 0.5 21 # 得到目标的结果列表,该列表和Y列表一一对应,因为X,Y,是对应的,res_li是x按位计算得来的,所以和Y也是对应的 22 res_li.append(dis_sum) 23 # 排序,取k个值 24 res_li1 = sorted(res_li)[:self.k] 25 # 获得前k个值对应的结果列表 26 # 排序后原来的对应关系被打乱,根据原来的res_li获得的index即为现在需要的index 27 res_y = [Y[res_li.index(i)] for i in res_li1] 28 # 内置方法:统计序列中相同个元素出现的个数,返回以元素,个数组合成的元组列表 29 return Counter(res_y).most_common(1)[0][0]
4.score方法:准确率计算
1 def score(train_X, train_Y, test_X, test_Y): 2 """ 3 做准确率的计算 4 :param train_X: 训练的特征矩阵 5 :param train_Y: 训练的目标向量 6 :param test_X: 测试的特征举证 7 :param test_Y: 测试的目标向量 8 :return: 测试后准确率 9 """ 10 count = 0 11 for index, value in enumerate(test_X): 12 test_i = class_ify(train_X, train_Y, value) 13 if test_i == test_Y[index]: 14 count += 1 15 return format(count / len(test_X), ".2%")
5.作为第四个方法的工具:随机分配训练集和测试集
1 def X_split(X, Y, split_size): 2 """ 3 根据split_size 随机分割X,Y 4 :param X: 特征矩阵 5 :param Y: 目标向量 6 :param split_size: 分割系数 7 :return: 训练集和测试集 (每个集合包括特征矩阵和目标向量) 8 """ 9 test_X, test_Y = [], [] 10 while len(test_X) <= len(Y) * split_size: 11 index = random.choice(range(len(X))) 12 test_X.append(X.pop(index)) 13 test_Y.append(Y.pop(index)) 14 return X, Y, test_X, test_Y
三、封装KNN框架
以上的代码可重用性还是很差,还是有冗余代码,所以我们要自己封装一个可重用性高,代码简洁的小框架。
参考request框架:实现多个功能,但每个功能的底层都是一样的
1.封装思路
KNN类:
属性:k
方法:
分类器 参数:特征矩阵,目标向量,测试数据
准确率计算 参数:训练集,测试集
Util类
方法
读取源数据,参数:filename,sep
特征归一化 参数:特征矩阵
训练集,测试集分割 参数:特征矩阵,目标向量,随机比例
以上只是我们参考前面的代码就能想出来的俩个类及其属性、方法
但是我们还要想一下,那就是我们的分类器是基于欧氏距离计算的,那要是别人想要用曼哈顿距离,余弦距离或者自定义的分类器呢,怎么办?
避免硬编码,我们需要向用户提供可重写的class_ify方法,但是根据原来的构思KNN类中还有准确率计算的方法,所以这个解决方法就是我们再写一个基类,来让KNN继承这个类
把准确率的算法放到基类中即可,下面是代码:
Base类和KNN类
1 class Base(): 2 # 该方法必须让子类重写 3 def class_ify(self, X, x, Y): 4 raise ValueError('class_ify方法必须重写!!!') 5 6 # 问题一、如何让这个方法不能重写 7 def score(self, train_X, train_Y, test_X, test_Y): 8 """ 9 做准确率的计算 10 :param train_X: 训练的特征矩阵 11 :param train_Y: 训练的目标向量 12 :param test_X: 测试的特征举证 13 :param test_Y: 测试的目标向量 14 :return: 测试后准确率 15 """ 16 count = 0 17 for index, value in enumerate(test_X): 18 test_i = self.class_ify(train_X, train_Y, value) 19 if test_i == test_Y[index]: 20 count += 1 21 return format(count / len(test_X), ".2%") 22 23 24 class KNN(Base): 25 def __init__(self, k): 26 self.k = k 27 28 def class_ify(self, X, Y, x): 29 """ 30 分类器 31 :param X:特征矩阵 32 :param Y:目标向量 33 :param x:测试数据 34 :return:测试数据的类别 35 """ 36 # 对测试数据x的容错处理 37 x_ = list(x) 38 x_1 = [float(i) for i in x_] 39 # 收集结果的列表 40 res_li = [] 41 # X是二位列表双层循环,第一层(外层)循环每一行,第二层(内层)循环列数,计算欧式距离 42 for i in X: 43 dis_sum = 0 44 for j in range(len(i)): 45 # 计算每个i与x的距离 46 dis_sum += (i[j] - x_1[j]) ** 2 47 dis_sum = dis_sum ** 0.5 48 # 得到目标的结果列表,该列表和Y列表一一对应,因为X,Y,是对应的,res_li是x按位计算得来的,所以和Y也是对应的 49 res_li.append(dis_sum) 50 # 排序,取k个值 51 res_li1 = sorted(res_li)[:self.k] 52 # 获得前k个值对应的结果列表 53 # 排序后原来的对应关系被打乱,根据原来的res_li获得的index即为现在需要的index 54 res_y = [Y[res_li.index(i)] for i in res_li1] 55 # 内置方法:统计序列中相同个元素出现的个数,返回以元素,个数组合成的元组列表 56 return Counter(res_y).most_common(1)[0][0]
Util 工具类
1 class Util(): 2 def load(self, filename, sep): 3 """ 4 读取元数据,并分离特征矩阵和目标向量 5 :param filename: 源文件路径 6 :return: Feature_matrix,aims_vector 特征矩阵 目标向量 7 """ 8 with open(filename, "r")as f: 9 res = f.readlines() 10 # 先用strip去除\n再用\t分离 11 res = [i.strip().split(sep) for i in res] 12 ##切割特征矩阵和目标向量 一般来说目标向量都在最后一列 13 # 目标向量 14 aims_vector = [i[-1] for i in res] 15 # 特征矩阵 16 Feature_matrix = [i[:-1] for i in res] 17 return Feature_matrix, aims_vector 18 19 def return_only(self, X): 20 ###方式一:不使用转置 ,直接改变原矩阵 21 for i in range(len(X[0])): 22 column = [float(x[i]) for x in X] 23 max_c, min_c = max(column), min(column) 24 # 改变原矩阵 25 for j in X: 26 j[i] = (float(j[i]) - min_c) / (max_c - min_c) 27 return X 28 ###方式二:使用矩阵的转置 29 # new_X = [] 30 # for i in range(len(X[0])): 31 # col = [float(x[i]) for x in X] 32 # max_col, min_col = max(col), min(col) 33 # new_col = [(c - min_col) / (max_col - min_col) for c in col] 34 # new_X.append(new_col) 35 # # 外层是转置后的行数,内层是转置后列数 36 # # 双层循环 内层在第一个 外层在第二个 37 # return [[new_X[i][j] for i in range(len(new_X))] for j in range(len(new_X[0]))] 38 39 def X_split(self, X, Y, split_size): 40 """ 41 根据split_size 随机分割X,Y 42 :param X: 特征矩阵 43 :param Y: 目标向量 44 :param split_size: 分割系数 45 :return: 训练集和测试集 (每个集合包括特征矩阵和目标向量) 46 """ 47 test_X, test_Y = [], [] 48 while len(test_X) <= len(Y) * split_size: 49 index = random.choice(range(len(X))) 50 test_X.append(X.pop(index)) 51 test_Y.append(Y.pop(index)) 52 return X, Y, test_X, test_Y
为了封装的更加彻底我们加上一执行类,保证类的完整性
1 class Cmx(): 2 # 面向客户的执行类 3 def __init__(self, result_filename, k=3, knn_cls=None): 4 """ 5 :param result_filename: 源数据文件 6 :param knn_cls: knn分类器cls,不指定使用默认值 7 :param k: knn的选择前几个 3,5,7 奇数 8 :return: 9 """ 10 self.result_filename = result_filename 11 self.k = k 12 self.knn_cls = knn_cls if knn_cls else KNN 13 14 def first_handler(self, sep): 15 # 实例化工具类 对源文件加工处理 16 util = Util() 17 X, Y = util.load(self.result_filename, sep) 18 # 最大最小归一化 19 X = util.return_only(X) 20 return X, Y 21 22 # 计算测试数据的所属类 23 def check_class(self, x, sep='\t'): 24 """ 25 :param x:待测试的数据 26 :param sep: 特征矩阵和目标向量的 分隔符 27 :param split_size: 训练集和测试的随机分类比例 【0-1】 28 :return: 目标的所属类 29 """ 30 X, Y = self.first_handler(sep) 31 # train_X, train_Y, test_X, test_Y = util.X_split(X, Y,split_size) 32 # 开始分类 33 return self.knn_cls(self.k).class_ify(X, Y, x) 34 35 # 计算准确率 36 def Accuracy(self, split_size=0.2, sep='\t'): 37 X, Y = self.first_handler(sep) 38 # 随机分配训练集和测试集 39 train_X, train_Y, test_X, test_Y = Util().X_split(X, Y, split_size) 40 res_sc = self.knn_cls(self.k).score(train_X, train_Y, test_X, test_Y) 41 return res_sc
测试代码:
1 result_filename = "【你的文件路径】\dating.txt" 2 cmx = Cmx(result_filename) 3 ##获得所属类 4 print(cmx.check_class((74676,14.445740))) 5 ##获得准确率 6 print(cmx.Accuracy(split_size=0.6)) 7 print(cmx.Accuracy(split_size=0.6)) 8 print(cmx.Accuracy(split_size=0.6))




