1 2 3 4

数据结构与算法学习笔记之如何分析一个排序算法？

前言

现在IT这块找工作，不会几个算法都不好意思出门，排序算法恰巧是其中最简单的，我接触的第一个算法就是它，但是你知道怎么分析一个排序算法么？有很多时间复杂度相同的排序算法，在实际编码中，那又如何选择呢？下面我们带着问题一起学习一下。

 正文

一、常见经典的排序方法

（图片来自于一像素）

插入排序

 

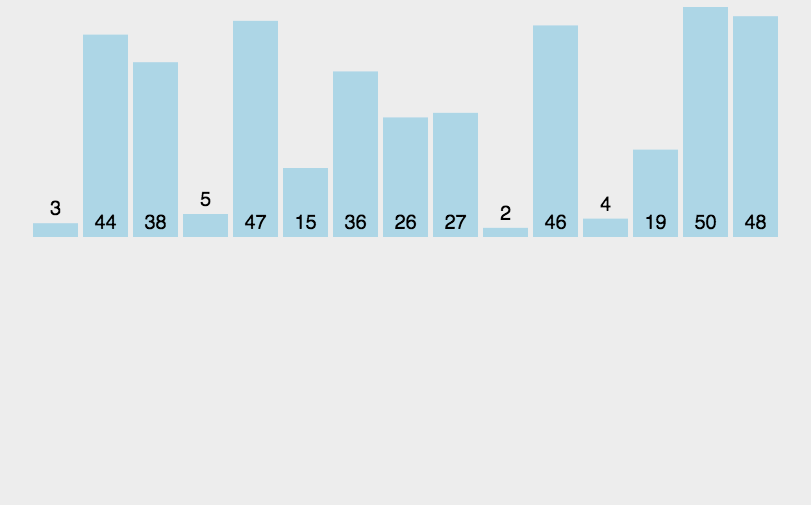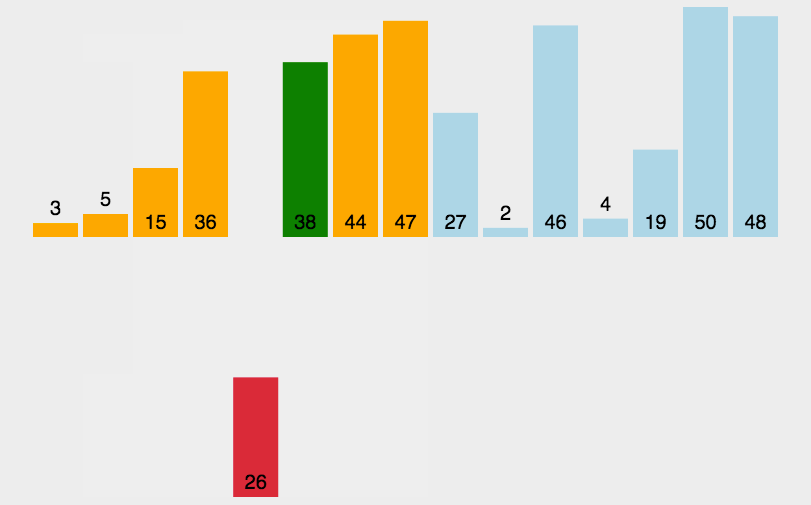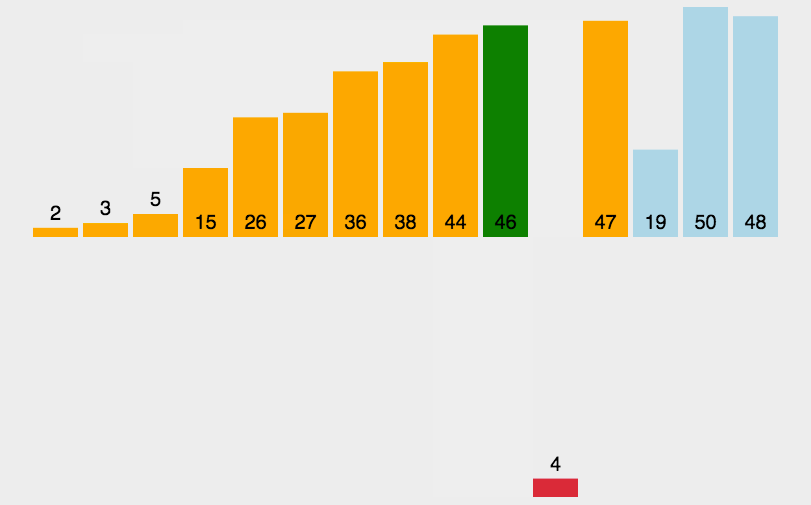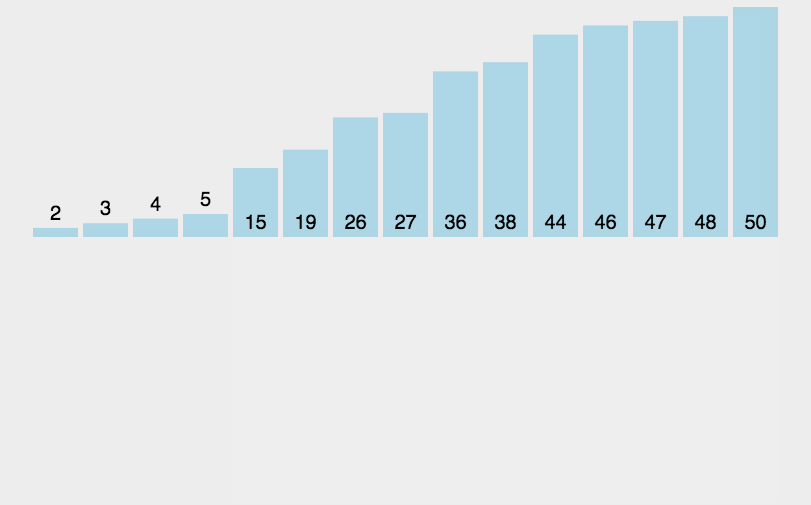
希尔排序（递减增量排序算法）

 

归并排序

快速排序

 

 

冒泡排序

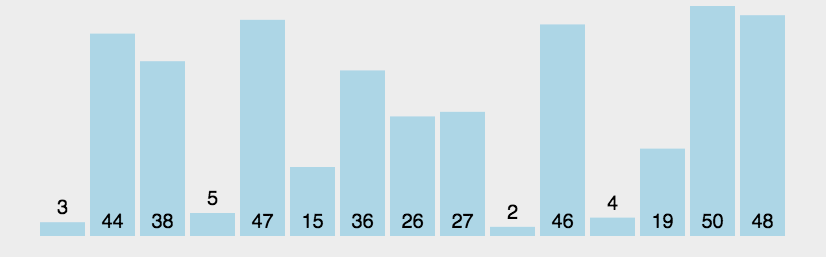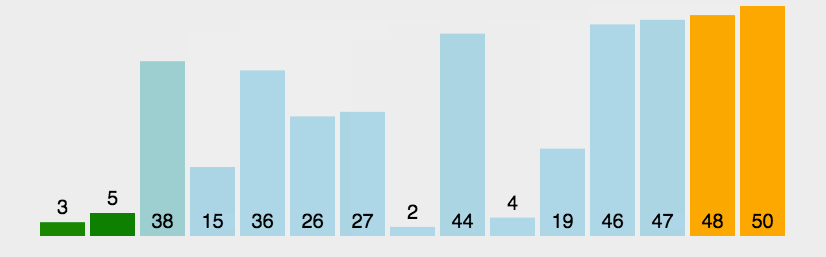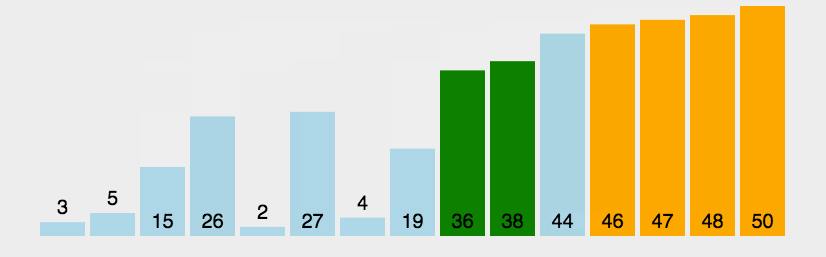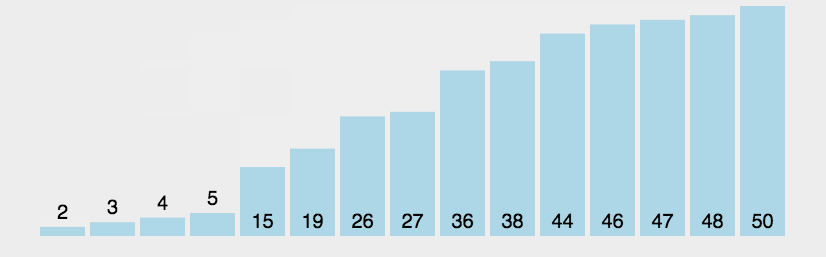
选择排序

计数排序

计数排序

堆排序

二、 按照时间复杂度归类

时间复杂度O（n2）：
冒泡排序、插入排序、选择排序 
 
时间复杂度O(nlogn)：
快速排序、归并排序
 
时间复杂度O(n)：
计数排序、基数排序、桶排序 

三、如何分析一个“排序算法”？

从三个方面入手

a、算法的执行效率

1.最好、最坏、平均情况时间复杂度。
从算法的核心，复杂度入手，给出最好最坏，平均情况下的时间复杂度，便于分析

2. 时间复杂度的系数、常数和低阶。
时间复杂度表示的是规模很大的一种增涨趋势，很容易就忽略系数，低阶，常数等，实际开发中排序的规模都是像10.100.1000这种小规模

3. 比较次数，交换（或移动）次数。
排序算法执行过程中，涉及两种操作，一种是元素比较大小，一种是元素交换或移动位置，所以比较次数，交换次数都得考虑进去。

b、排序算法的内存消耗

算法消耗可以通过空间复杂度来衡量

原地排序算法：特指空间复杂度是O(1)的排序算法。

c、排序算法的稳定性

1. 稳定性概念：如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。
2. 稳定性重要性：可针对对象的多种属性进行有优先级的排序。
3. 举例：给电商交易系统中的“订单”排序，按照金额大小对订单数据排序，对于相同金额的订单以下单时间早晚排序。用稳定排序算法可简洁地解决。先按照下单时间给订单排序，排序完成后用稳定排序算法按照订单金额重新排序。


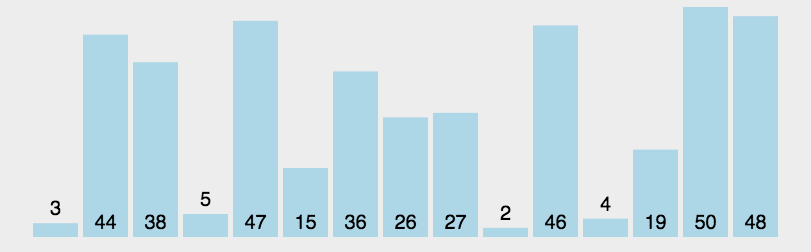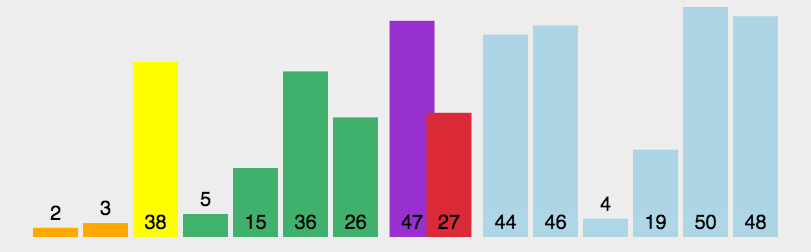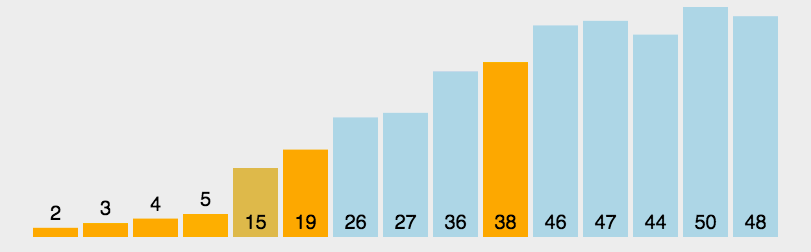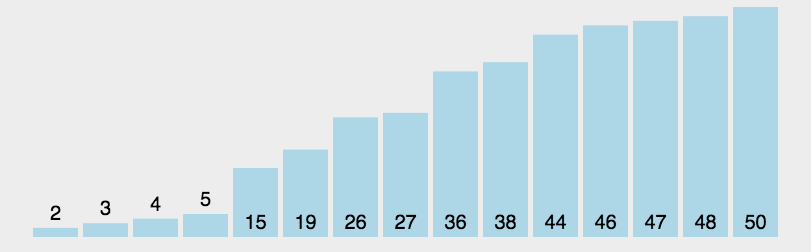
四、详解冒泡排序

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求，如果不满足就让它俩互换。
 
冒泡排序只涉及相邻数据的交换，只需要常量级的临时空间，所以它的空间复杂度未O（1）是原地排序算法
 
稳定性：当有相邻的两个元素大小相等时，不做交换，冒泡排序是稳定的排序算法。
 
引入两个概念：
默认从小到大未有序
有序度：数组中具有有序关系的元素对的个数。
满有序度：完全有序的数组
逆序度：数组中具有无序关系的元素对的个数。
逆序度=满有序度-有序度
排序的过程实际上就是增加有序度，减少逆序度的过程
 
时间复杂度：
1. 最好情况（满有序度）：O(n)。
2. 最坏情况（满逆序度）：O(n^2)。
3. 平均情况：
“有序度”和“逆序度”：对于一个不完全有序的数组，如4，5，6，3，2，1，有序元素对为3个（4，5），（4，6），（5，6），有序度为3，逆序度为12；对于一个完全有序的数组，如1，2，3，4，5，6，有序度就是n*(n-1)/2，也就是15，称作满有序度；逆序度=满有序度-有序度；冒泡排序、插入排序交换（或移动）次数=逆序度。
最好情况下初始有序度为n*(n-1)/2，最坏情况下初始有序度为0，则平均初始有序度为n*(n-1)/4，即交换次数为n*(n-1)/4，因交换次数<比较次数<最坏情况时间复杂度，所以平均时间复杂度为O(n2)。
 
代码实现：
// 冒泡排序，a 表示数组，n 表示数组大小
public void bubbleSort(int[] a, int n) {
  if (n <= 1) return;
 
 for (int i = 0; i < n; ++i) {
    // 提前退出冒泡循环的标志位
    boolean flag = false;
    for (int j = 0; j < n - i - 1; ++j) {
      if (a[j] > a[j+1]) { // 交换
        int tmp = a[j];
        a[j] = a[j+1];
        a[j+1] = tmp;
        flag = true;  // 表示有数据交换      
      }
    }
    if (!flag) break;  // 没有数据交换，提前退出
  }
}

 

 

五、详解插入排序

将数据分为两个区间，已排序区间和未排序区间，初始已排序区间只有一个元素(即第一个数据)，我们取未排序区间的元素，在已排序的区间中找到合适的位置插入位置插入，并保证已排序区间数据一直有序，重复过程，直到未排序区间中没有元素

运行过程中看得出来，不需要额外的存储空间，所以空间复杂度为0（1），也是原地排序算法

同样值的元素，前后顺序保持不变，是稳定的排序算法

时间复杂度：

最好时间复杂度为O(n)

最坏时间复杂度为O(n2)

平均时间复杂度为O(n2)

代码实现：

// 插入排序，a 表示数组，n 表示数组大小
public void insertionSort(int[] a, int n) {
  if (n <= 1) return;

  for (int i = 1; i < n; ++i) {
    int value = a[i];
    int j = i - 1;
    // 查找插入的位置
    for (; j >= 0; --j) {
      if (a[j] > value) {
        a[j+1] = a[j];  // 数据移动
      } else {
        break;
      }
    }
    a[j+1] = value; // 插入数据
  }
}

 

六、详解选择排序

选择排序将数组数据分成已排序区间和未排序区间。初始已排序区间只有一个元素，即数组第一个元素。在未排序区间找到最小的数据，将其放在已排序区间的末尾

空间复杂度为O(1)，选择排序是原地排序算法。
 
未排序区间的元素和已排序区间的元素相同时，它可以放在已排序区间相同值的前或后，所以为不稳定的排序

时间复杂度：
1. 最好情况：O(n2)。
2. 最坏情况：O(n2)。
3. 平均情况：O(n2)（往数组中插入一个数的平均时间复杂度是O(n)，一共重复n次）。

七、各种排序方法的汇总比较


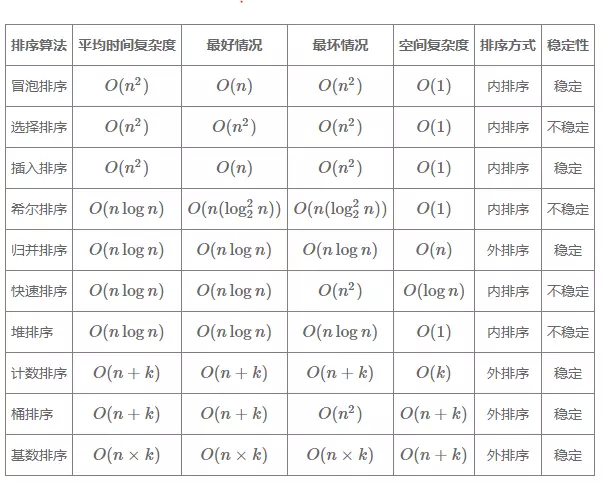
八、选择排序和插入排序的时间复杂度相同，都是O(n^2)，在实际的软件开发中，为什么我们更倾向于使用插入排序而不是冒泡排序算法呢？

答：它们的元素比较次数以及交换元素的次数都是原始数据的逆序度，是一个固定值，但是从代码实现上来看，冒泡排序的数据交换要比插入排序的数据移动要复杂，冒泡排序需要3个赋值操作，而插入排序只需要1个，他们 的时间复杂度上都是O(n2)，但是为了追求极致的性能，所以首选插入排序算法
 

结尾

大家不妨试着分析一下其他的几种算法。

看再多遍都不如写一篇来得深刻，建议大家多敲。

相关文章

数据结构与算法学习笔记之写链表代码的正确姿势（下）

数据结构与算法学习笔记之 提高读取性能的链表（上）

数据结构与算法学习笔记之 从0编号的数组

数据结构与算法学习笔记之后进先出的“桶”

数据结构与算法学习笔记之先进先出的队列

数据结构与算法学习笔记之高效、简洁的编码技巧“递归”

以上内容为个人的学习笔记，仅作为学习交流之用。

 

欢迎大家关注公众号，不定时干货，只做有价值的输出

作者：Dawnzhang 
出处：https://www.cnblogs.com/clwydjgs/p/9815690.html

版权：本文版权归作者
转载：欢迎转载，但未经作者同意，必须保留此段声明；必须在文章中给出原文连接；否则必究法律责任

posted @ 2018-10-19 16:20  Dawnzhang  阅读(1079)  评论(1)  编辑  收藏  举报
PV