公钥密码之RSA
鱼跃此时海,花开彼岸天。
算法分析
- RSA是最早的公钥密码系统之一, 广泛用于安全数据传输。
- RSA的基础是数论的欧拉定理,它的安全性依赖于大整数因式分解的困难性。
- RSA算法主要由密钥生成、加密和解密三个部分组成。
- 密钥生成:
a 选择两个大素数𝑝和𝑞,(𝑝≠𝑞,需要保密,步骤4以后建议销毁)
b 计算𝑛=𝑝×𝑞,φ(n) =(𝑝-1)×(𝑞-1)
c 选择整数 𝑒 使(φ(n),𝑒) =1,1<𝑒< φ(n)
d 计算𝑑,使𝑑 = e^(-1) (modφ(n)), 得到:公钥为{𝑒, 𝑛}; 私钥为{𝑑} - 加密:
用𝒆,𝒏: 明文𝑀<𝑛, 密文𝐶=M^e (𝑚𝑜𝑑 𝑛) - 解密:
用𝒅,𝒏: 密文𝐶, 明文𝑀 =C^d (𝑚𝑜𝑑 𝑛)
算法实现
# 欧几里得算法求两个数字的最大公约数
def gcd(a, b):
if b == 0:
return a
else:
return gcd(b, a % b)
'''
扩展欧几里的算法
计算 ax + by = 1中的x与y的整数解(a与b互质)
gcd(a, b) = a*xi + b*yi
gcd(b, a % b) = b*xi+1 + (a - [a/b]*b)*yi+1
gcd(a, b) = gcd(b, a % b) => a*xi + b*yi = a*yi+1 + b*(xi+1 - [a/b]*yi+1)
xi = yi+1
yi = xi+1 - [a/b]*yi+1
'''
def ext_gcd(a, b):
if b == 0:
x1 = 1
y1 = 0
x = x1
y = y1
r = a
return r, x, y
else:
r, x1, y1 = ext_gcd(b, a % b)
x = y1
y = x1 - (a // b ) * y1
return r, x, y
# 使用快速幂取模计算法进行加密解密
def power(a, b, c):
s = 1
a %=c
while b !=0:
if b % 2 ==1:
s = (s * a) % c
b = b // 2
a = (a * a) % c
return s
# 生成公钥私钥,p、q为两个超大质数
def gen_key(p, q):
n = p * q
fn = (p - 1) * (q - 1) # 计算与n互质的整数个数 欧拉函数
e = 3889
a = e
b = fn
r, x, y = ext_gcd(a, b)
print("选取的公钥为: \n", e)
print("生成的私钥为: \n", x)
d = x
# 返回公钥 私钥
return (n, e), (n, d)
# 加密 m是被加密的信息 加密成为c
def encrypt(m, pubkey):
n = pubkey[0]
e = pubkey[1]
c = power(m, e, n)
return c
# 解密 c是密文,解密为明文m
def decrypt(c, selfkey):
n = selfkey[0]
d = selfkey[1]
m = power(c, d, n)
return m
if __name__ == "__main__":
'''公钥私钥中用到的两个大素数数p,q,都是1024位'''
p = 106697219132480173106064317148705638676529121742557567770857687729397446898790451577487723991083173010242416863238099716044775658681981821407922722052778958942891831033512463262741053961681512908218003840408526915629689432111480588966800949428079015682624591636010678691927285321708935076221951173426894836169
q = 144819424465842307806353672547344125290716753535239658417883828941232509622838692761917211806963011168822281666033695157426515864265527046213326145174398018859056439431422867957079149967592078894410082695714160599647180947207504108618794637872261572262805565517756922288320779308895819726074229154002310375209
'''生成公钥私钥'''
pub_key, self_key = gen_key(p, q)
'''需要被加密的信息转化成数字,长度小于n的长度,如果信息长度大于n的长度,那么分段进行加密,分段解密即可。'''
m = 1356205320457610288745198967657644166379972189839804389074591563666634066646564410685955217825048626066190866536592405966964024022236587593447122392540038493893121248948780525117822889230574978651418075403357439692743398250207060920929117606033490559159560987768768324823011579283223392964454439904542675637683985296529882973798752471233683249209762843835985174607047556306705224118165162905676610067022517682197138138621344578050034245933990790845007906416093198845798901781830868021761765904777531676765131379495584915533823288125255520904108500256867069512326595285549579378834222350197662163243932424184772115345
print("明文为: \n", m)
'''信息加密,m被加密的信息,c是加密后的信息'''
c = encrypt(m, pub_key)
print("加密后的密文为: \n", c)
'''信息解密'''
d = decrypt(c, self_key)
print("解密后的明文为: \n", d)
加密与解密
公钥私钥中用到的两个大素数数p,q,都是1024位,首先生成相应的公钥和私钥。然后,将需要被加密的信息转化成十进制,长度小于n的长度,如果信息长度大于n的长度,那么分段进行加密,分段解密即可。具体例子如下:
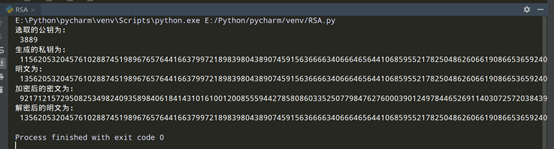
正确性
证明接收者可以使用私钥及解密算法恢复出明文。分两种情况讨论:

安全性分析
- RSA的安全性依赖于大数分解,但是否等同于大数分解一直未能得到理论上的证明,因为没有证明破解RSA就一定需要作大数分解。
- 对于RSA的攻击,存在以下攻击:
- 针对𝑛分解的攻击,需要完全尝试所有小于√n的素数。
- 循环攻击:攻击者得到密文𝑐后,对密文𝑐依次进行如下变换:

- 共模攻击:假设𝑚是明文,两用户的公钥分别是𝑒1和𝑒2,且(𝑒1,𝑒2)=1,共同的模数𝑁,两个密文分别为:

知道𝑁,𝑒1,𝑒2,𝑐1和𝑐2,可如下恢复明文𝑚。
(𝑒1,𝑒2)=1,由欧几里德算法可找出𝑟,𝑠满足𝑟𝑒1+𝑠𝑒2=1。
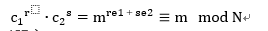
无需秘密密钥𝑑,就可以得到明文𝑚 - 选择密文攻击:需要破译密文和骗取签名。
RSA模幂运算的性质:

- 用户A公钥为
(𝑒,𝑛),攻击者监听到发给A的密文𝑐=𝑚^𝑒 𝑚𝑜𝑑 𝑛 - 攻击者随机选取一个
𝑟 <𝑛,计算𝑦=𝑟^𝑒 𝑚𝑜𝑑 𝑛,𝑡=𝑦𝑐 (𝑚𝑜𝑑 𝑛) - 攻击者发送𝑡给A,要求A对消息𝑡签名(A用私钥签名)
- A把签名返回给攻击者,攻击者就得到了
𝑠=𝑡^𝑑 𝑚𝑜𝑑 𝑛攻击者计算:
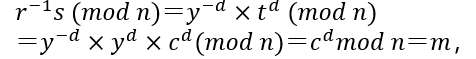
于是攻击者获得了明文𝑚
- 低加密指数攻击:小的公钥可加快加密的速度,但过小的公钥易受到攻击。
- 如果3个用户都使用3作为公钥,对同一个明文𝑚加密,则
c1=m3 (mod n1),c2=m3 (mod n2),c3=m3 (mod n3), gcd(n1,n2,n3)=1,且𝑚<𝑛1,𝑚<𝑛2,𝑚<𝑛3 - 由中国剩余定理可从
𝑐1,𝑐2,𝑐3计算出𝑐,且c=m3 mod (n1n2n3 ),显然m3<n1n2n3,所以m=c^(1/3)
- 时间攻击:时间攻击主要针对RSA核心运算是非常耗时的模乘,只要能够精确监视RSA的解密过程,就能估算出私有密钥𝑑。
感谢阅读,如有问题,请批评指正,谢谢。

